华师大版数学八年级下册17.5 实践与探索 同步测试
试卷更新日期:2024-03-13 类型:同步测试
一、选择题
-
1. 观察下列表格的对应值,则关于的方程(为常数)解的取值范围是( ).
2.13
2.14
2.15
2.16
0.04
0.01
A、 B、 C、 D、2. 如图,直线:与直线:交于点 , 则不等式的解集是( ) A、 B、 C、 D、3. 已知一次函数的图象过点 , 则不等式的解集是( )A、 B、 C、 D、4. 如图,在同一平面直角坐标系中,一次函数与 , 小聪根据图象得到如下结论:
A、 B、 C、 D、3. 已知一次函数的图象过点 , 则不等式的解集是( )A、 B、 C、 D、4. 如图,在同一平面直角坐标系中,一次函数与 , 小聪根据图象得到如下结论:①;②关于x,y的方程组的解为;③关于x的方程的解为;④关于x的不等式的解集是 .
其中结论正确的个数是( )
 A、1 B、2 C、3 D、45. 如图,在平面直角坐标系中,直线与直线相交于点 , 则关于 , 的二元一次方程组的解是( )
A、1 B、2 C、3 D、45. 如图,在平面直角坐标系中,直线与直线相交于点 , 则关于 , 的二元一次方程组的解是( ) A、 B、 C、 D、6. 如图,已知函数 和 的图象交于点 ,则根据图象可得不等式 的解集是( )
A、 B、 C、 D、6. 如图,已知函数 和 的图象交于点 ,则根据图象可得不等式 的解集是( )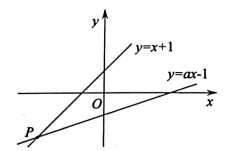 A、 B、 C、 D、7. 如图,函数和的图像交于点P , 根据图像可得不等式的解集是( )
A、 B、 C、 D、7. 如图,函数和的图像交于点P , 根据图像可得不等式的解集是( ) A、 B、 C、 D、8. 如图,一次函数y=ax+b(a≠0)与反比例函数y 的图象相交于点A(1,2),B(m,-1),则关于x的不等式 的解是( )
A、 B、 C、 D、8. 如图,一次函数y=ax+b(a≠0)与反比例函数y 的图象相交于点A(1,2),B(m,-1),则关于x的不等式 的解是( ) A、x<-2或0<x<1 B、x<-1或0<x<2 C、-2<x<0或x>1 D、-1<x<0或x>29. 在平面直角坐标系xOy中,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=相交于点A,B,且AC+BC=4,则△OAB的面积为( )A、2+或2- B、2+2或2-2 C、2- D、2+210. 已知一次函数( , k是常数),则下列结论正确的是( )A、若点在一次函数的图象上,则它的图象与两个坐标轴围成的三角形面积是2; B、若 , 则一次函数图象上任意两点和满足: C、一次函数的图象不一定经过第三象限 D、若对于一次函数和 , 无论x取任何实数,总有 , 则k的取值范围是或11. 如图,在平面直角坐标系中,矩形的点和点分别落在轴和轴正半轴上, , 直线经过点 , 将直线向下平移个单位,若直线可将矩形的面积平分,则的值为( )
A、x<-2或0<x<1 B、x<-1或0<x<2 C、-2<x<0或x>1 D、-1<x<0或x>29. 在平面直角坐标系xOy中,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=相交于点A,B,且AC+BC=4,则△OAB的面积为( )A、2+或2- B、2+2或2-2 C、2- D、2+210. 已知一次函数( , k是常数),则下列结论正确的是( )A、若点在一次函数的图象上,则它的图象与两个坐标轴围成的三角形面积是2; B、若 , 则一次函数图象上任意两点和满足: C、一次函数的图象不一定经过第三象限 D、若对于一次函数和 , 无论x取任何实数,总有 , 则k的取值范围是或11. 如图,在平面直角坐标系中,矩形的点和点分别落在轴和轴正半轴上, , 直线经过点 , 将直线向下平移个单位,若直线可将矩形的面积平分,则的值为( ) A、11 B、9 C、6 D、512. 如图,在平面直角坐标系中,点 , , , 都在轴上,点 , , , 都在直线上, , , , 都是等腰直角三角形,且 , 则点的坐标是( )
A、11 B、9 C、6 D、512. 如图,在平面直角坐标系中,点 , , , 都在轴上,点 , , , 都在直线上, , , , 都是等腰直角三角形,且 , 则点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,正方形 , , , …的顶点 , , , …在直线上,顶点 , , , …在x轴上,已知 , , 那么点的坐标为.
 14. 一次函数(为常数,且)中的与的部分对应值如下表:
14. 一次函数(为常数,且)中的与的部分对应值如下表:2
0
下列结论中:①方程的解为;②若 , 则;③若的解为 , 则;④若关于的不等式的解集为 , 则 . 一定正确的是 .
15.如图:函数y=2x和y=ax+4的图象交于点A(m,2),不等式2x<ax+4的解集为 .
 16. 在平面直角坐标系中,一次函数与的图象的交点坐标是 , 则方程组的解是 .17. 如图,已知函数与函数的图象交于点 , 则方程组的解是 .
16. 在平面直角坐标系中,一次函数与的图象的交点坐标是 , 则方程组的解是 .17. 如图,已知函数与函数的图象交于点 , 则方程组的解是 . 18. 如图,A,C是正比例函数y=x的图象与反比例函数 的图象的交点,过点A作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD的周长为.
18. 如图,A,C是正比例函数y=x的图象与反比例函数 的图象的交点,过点A作AD⊥x轴于点D,过点C作CB⊥x轴于点B,则四边形ABCD的周长为.
三、解答题
-
19. 如图,一次函数图象与反比例函数图象交于点A(-1,6),B( , a-3),与x轴交于点C,与y轴交于点D.
 (1)、求反比例函数与一次函数的表达式;(2)、点M在x轴上,若S△OAM=S△OAB , 求点M的坐标.20. 如图,直线y=x-3与x轴交于点C,与y轴交于点D,直线y=kx+b与y轴交于点B(0,4),与直线y=x-3交于点A(m,1).
(1)、求反比例函数与一次函数的表达式;(2)、点M在x轴上,若S△OAM=S△OAB , 求点M的坐标.20. 如图,直线y=x-3与x轴交于点C,与y轴交于点D,直线y=kx+b与y轴交于点B(0,4),与直线y=x-3交于点A(m,1). (1)、求直线AB的表达式;(2)、点P是直线CD上的一个动点,连接PB,当△PBA的面积为7时,求点P的坐标;(3)、E为y轴上的点,F在坐标平面内,以点A,B,E,F为顶点的四边形是菱形,请直接写出符合条件的点F的坐标.21. 已知:在平面直角坐标系中,直线与x轴,y轴分别交于A、B两点,直线经过点A,与y轴交于点 .
(1)、求直线AB的表达式;(2)、点P是直线CD上的一个动点,连接PB,当△PBA的面积为7时,求点P的坐标;(3)、E为y轴上的点,F在坐标平面内,以点A,B,E,F为顶点的四边形是菱形,请直接写出符合条件的点F的坐标.21. 已知:在平面直角坐标系中,直线与x轴,y轴分别交于A、B两点,直线经过点A,与y轴交于点 . (1)、求直线的解析式;(2)、点P为直线上的一个动点.若的面积等于10时,请求出点P的坐标;22. 为响应国家“电商助农”的号召,某电商平台准备将本地农户合作社手工制作的具有本地文化特色的衬衣和T恤衫进行线上销售,它们的进价和售价如下表已知购进一件衬衣比一件T恤衫的进价贵元,用元恰好可购进衬衣件和T恤衫件.
(1)、求直线的解析式;(2)、点P为直线上的一个动点.若的面积等于10时,请求出点P的坐标;22. 为响应国家“电商助农”的号召,某电商平台准备将本地农户合作社手工制作的具有本地文化特色的衬衣和T恤衫进行线上销售,它们的进价和售价如下表已知购进一件衬衣比一件T恤衫的进价贵元,用元恰好可购进衬衣件和T恤衫件.种类
衬衣
T恤衫
进价元件
售价元件
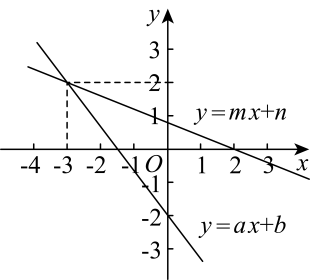
(1)、分别求出表中和的值;(2)、若该电商计划购进衬衣和T恤衫两种服饰共件,据市场销售分析,T恤衫进货件数不低于衬衣件数的倍如何进货才能使木次销售获得的利润最大?最大利润是多少元?23. 一次函数和的图象如图所示,且 , . (1)、观察图象,直接写出不等式的解集;(2)、若不等式的解集是 , 求点C的坐标.
(1)、观察图象,直接写出不等式的解集;(2)、若不等式的解集是 , 求点C的坐标.

