2024年江苏省南京中考数学仿真模拟卷
试卷更新日期:2024-03-13 类型:中考模拟
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 实数9的算术平方根是( )A、3 B、 C、 D、2. 我国自行设计、自主集成研制的蛟龙号载人潜水器最大下潜深度为7062m.将7062用科学记数法表示为( )A、7.062×103 B、7.1×103 C、0.7062×104 D、7.062×1043. 如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
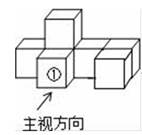 A、主视图改变,俯视图改变 B、左视图改变,俯视图改变 C、俯视图不变,左视图改变 D、主视图不变,左视图不变4. 将方程x2﹣2x﹣3=0化为(x﹣m)2=n的形式,指出m,n分别是( )A、1和3 B、﹣1和3 C、1和4 D、﹣1和45.
A、主视图改变,俯视图改变 B、左视图改变,俯视图改变 C、俯视图不变,左视图改变 D、主视图不变,左视图不变4. 将方程x2﹣2x﹣3=0化为(x﹣m)2=n的形式,指出m,n分别是( )A、1和3 B、﹣1和3 C、1和4 D、﹣1和45.如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )
 A、24 B、9 C、36 D、276. 已知二次函数y=ax2+bx+c,其函数y与自变量x之间的部分对应值如表所示:
A、24 B、9 C、36 D、276. 已知二次函数y=ax2+bx+c,其函数y与自变量x之间的部分对应值如表所示:X
…
﹣1
2
3
…
Y
…
0
0
4
…
则可求得 (4a﹣2b+c)的值是( )
A、8 B、﹣8 C、4 D、﹣4二、填空题(本大题共10小题,共20.0分)
-
7. 当x=时,分式 的值为零.8. 计算:的结果为 .9. 如图,直线 , 若 , , , 则的长为 .
 10. 已知扇形的面积为15πcm2 , 弧长为5πcm,则该扇形的圆心角是度.11. 已知a , b是方程3x2﹣6x+2=0的两个根,则a2+b2= .12. 已知一组数据:的平均数是2,方差是3,另一组数据: , , …的方差是
10. 已知扇形的面积为15πcm2 , 弧长为5πcm,则该扇形的圆心角是度.11. 已知a , b是方程3x2﹣6x+2=0的两个根,则a2+b2= .12. 已知一组数据:的平均数是2,方差是3,另一组数据: , , …的方差是
13. 分解因式:2ab2+4ab+2a= .14. 如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=70°,则∠EAC的度数为. 15. 规定:两个函数 , 的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数 与 的图象关于y轴对称,则这两个函数互为“Y函数”.若函数 (k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为.16. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则线段EF的最小值为 .
15. 规定:两个函数 , 的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数 与 的图象关于y轴对称,则这两个函数互为“Y函数”.若函数 (k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为.16. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则线段EF的最小值为 .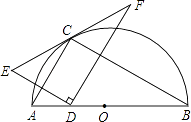
三、计算题(本大题共2小题,共16.0分)
-
17. 解不等式组:18. 解分式方程: .
四、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 先化简,再求值: ,其中 .20. 如图,延长正方形 的一边 至点 与 相交于点F,过点F作 交 于点G.求证: .
 21. 在一个不透明的布袋里装有3个标号为1、2、3的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的2个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).(1)、请你运用画树状图或列表的方法,写出点P所有可能的坐标;(2)、求点P(x,y)在函数y=-x+3图象上的概率.22. 2023年4月24日中国航天日主场活动暨中国航天大会在合肥市开幕,今年中国航天日的主题是“格物致知,叩问苍穹”.某学校为了解八年级学生对航空航天知识的了解情况,组织了一次知识竞赛活动,从两班各随机抽取了10名学生的成绩,整理如下:(成绩得分用表示,共分成四组:A. , B. , C. , D. )
21. 在一个不透明的布袋里装有3个标号为1、2、3的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的2个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).(1)、请你运用画树状图或列表的方法,写出点P所有可能的坐标;(2)、求点P(x,y)在函数y=-x+3图象上的概率.22. 2023年4月24日中国航天日主场活动暨中国航天大会在合肥市开幕,今年中国航天日的主题是“格物致知,叩问苍穹”.某学校为了解八年级学生对航空航天知识的了解情况,组织了一次知识竞赛活动,从两班各随机抽取了10名学生的成绩,整理如下:(成绩得分用表示,共分成四组:A. , B. , C. , D. )八年级(1)班10名学生的成绩是:96,80,96,86,99,98,92,100,89,84.
八年级(2)班10名学生的成绩在C组中的数据是:94,90,92.
通过数据分析,列表如下:
八年级(1)班、(2)班抽取的学生竞赛成绩统计表
班级
平均数
中位数
众数
方差
八年级(1)班
92
43.4
八年级(2)班
92
93
100
50.4
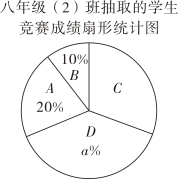
根据以上信息,解答下列问题:
(1)、填空: , , ;(2)、学校欲选派成绩比较稳定的班级参加下一阶段的活动,根据表格中的数据,学校会选派哪一个班级?请说明理由;(3)、已知八年级两个班共120人参加了此次竞赛活动,估计两班参加此次竞赛活动成绩优秀的学生总人数是多少?23. 在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示: (1)、试判断y与x之间的函数关系,并求出函数关系式;(2)、若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;(3)、在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.24. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).
(1)、试判断y与x之间的函数关系,并求出函数关系式;(2)、若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;(3)、在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.24. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).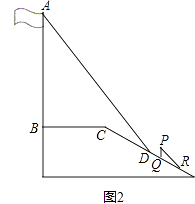 25. 如图1,四边形ABCD内接于⊙O , BD为直径, 上存在点E, 满足 , 连结BE并延长交CD的延长线于点F , BE与AD交于点G.
25. 如图1,四边形ABCD内接于⊙O , BD为直径, 上存在点E, 满足 , 连结BE并延长交CD的延长线于点F , BE与AD交于点G.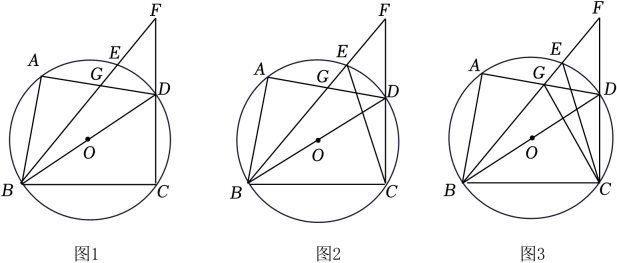 (1)、若∠DBC=α,请用含α的代数式表示∠AGB;(2)、如图2,连结CE , CE=BG . 求证:EF=DG;(3)、如图3,在(2)的条件下,连结CG , AD=2,求CG的最小值.26.
(1)、若∠DBC=α,请用含α的代数式表示∠AGB;(2)、如图2,连结CE , CE=BG . 求证:EF=DG;(3)、如图3,在(2)的条件下,连结CG , AD=2,求CG的最小值.26.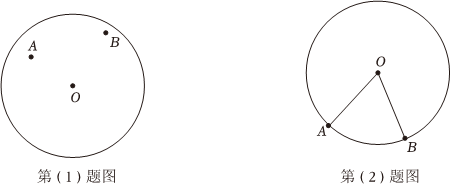 (1)、已知:如图,、是内两点,求作:的直径 , 使 .(2)、已知:如图,、是的半径,求作:弦 , 使其与、的交点是的三等分点要求:尺规作图,保留作图痕迹,写出必要的文字说明27. 综合与实践
(1)、已知:如图,、是内两点,求作:的直径 , 使 .(2)、已知:如图,、是的半径,求作:弦 , 使其与、的交点是的三等分点要求:尺规作图,保留作图痕迹,写出必要的文字说明27. 综合与实践车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做成圆形的呢?这里面有什么数学道理吗?带着这样的疑问,小青做了如下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.
 (1)、探究一:将车轮设计成等边三角形,转动过程如图1,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图2中计算C到的距离.(2)、探究二:将车轮设计成正方形,转动过程如图3,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图4中计算C到的距离(结果保留根号).(3)、探究三:将车轮设计成正六边形,转动过程如图5,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),在图6中计算C到的距离(结果保留根号).(4)、归纳推理:比较 , , 大小: , 按此规律推理,车轮设计成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线(水平线)的距离(填“越大”或“越小”).(5)、得出结论:将车轮设计成圆形,转动过程如图7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)的距离.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.
(1)、探究一:将车轮设计成等边三角形,转动过程如图1,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图2中计算C到的距离.(2)、探究二:将车轮设计成正方形,转动过程如图3,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),请在图4中计算C到的距离(结果保留根号).(3)、探究三:将车轮设计成正六边形,转动过程如图5,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是 , 圆心角.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是(水平线),在图6中计算C到的距离(结果保留根号).(4)、归纳推理:比较 , , 大小: , 按此规律推理,车轮设计成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线(水平线)的距离(填“越大”或“越小”).(5)、得出结论:将车轮设计成圆形,转动过程如图7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)的距离.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.