2024春季苏科版数学七下第七、八章周测卷

试卷更新日期：2024-03-13 类型：复习试卷

进入出卷网下载

一、选择题

1.
下列所示的四个图形中，∠1和∠2是同位角的是（）

A、②③ B、①②③ C、①②④ D、①④

查看试题解析
2. 如图，点E在BA延长线上，下列条件不能判断 $A B ∥ C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ E A D = ∠ A D C$ C、 $∠ 3 = ∠ 4$ D、 $∠ C + ∠ A B C = 180 °$

查看试题解析
3. 如图，如果 $∠ 1 = ∠ 2$ ，那么 $A B ∥ C D$ ，其依据可以简单说成（）

A、两直线平行，内错角相等 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、同位角相等，两直线平行

查看试题解析
4. 如图，已知 $A B / / C D$ ， $O E$ 平分 $∠ B O C$ ， $O F ⊥ O E$ ， $O P ⊥ C D$ .若 $∠ A B O = α °$ ，给出下列结论：① $∠ B O E = \frac{1}{2} (180 - α) °$ ；② $O F$ 平分 $∠ B O D$ ；③ $∠ P O E = ∠ B O F$ ；④ $∠ P O B = 2 ∠ D O F$ .其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，直线a、b被直线c所截，下列说法正确的是（）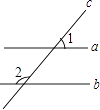

A、当∠1=∠2时，一定有a∥b B、当a∥b时，一定有∠1=∠2 C、当a∥b时，一定有∠1+∠2=90° D、当∠1+∠2=180°时，一定有a∥b

查看试题解析
6. 要得知作业纸上两相交直线 $A B$ 、 $C D$ 所夹锐角的大小，发现其交点不在作业纸内，无法直接测量．两同学提供了如下间接测量方案 $($ 如图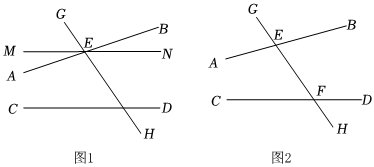 $1$ 和图 $2)$ ：
对于方案Ⅰ、Ⅱ，说法正确的是（）
方案Ⅰ： $①$ 作一直线 $G H$ ，交 $A B$ 、 $C D$ 于点 $E$ ， $F$ ；
      $②$ 利用尺规作 $∠ H E N = ∠ C F G$ ；
      $③$ 测量 $∠ A E M$ 的大小即可．
方案Ⅱ： $①$ 作一直线 $G H$ ，交 $A B$ 、 $C D$ 于点 $E$ ， $F$ ；
      $②$ 测量 $∠ A E H$ 和 $∠ C F G$ 的大小；
      $③$ 计算 $180 ° - ∠ A E H - ∠ C F G$ 即可．

A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行

查看试题解析

二、填空题

7. 如图，光线在不同介质中的传播速度是不同的，因此当光线从空气射向水中时，要发生折射．由于折射率相同，所以在空气中平行的光线，在水中也是平行的．若∠1＝56°，∠2＝112°，则∠3的大小为度．

查看试题解析
8. 如图，直线a、b被直线c、d所截．若 $∠ 1 = ∠ 2 = ∠ 3 = 50 °$ ，则 $∠ 4$ 的大小是度．

查看试题解析
9. 如图， $A B / / C D$ ，直线 $E F$ 经过点 $C$ ， $∠ D C E = 65 °$ ， $∠ A C F = 10 °$ ，则 $∠ A =$ ．

查看试题解析
10. 如图是小明学习“探索直线平行的条件”时用到的学具，经测量 $∠ 2 = 105 °$ ，要使木条a与b平行，则 $∠ 1$ 的度数应为°.

查看试题解析
11. 如图，已知∠1=∠2，∠3=40°，则∠4= °

查看试题解析
12. 两个角α和β的两边互相平行，且一个角α比另一个角β的 $\frac{1}{3}$ 多20°，则这个角α的度数为度．

查看试题解析
13. 如图，A岛在B岛的北偏东30°方向，C岛在B岛的北偏东80°方向，A岛在C岛北偏西40°方向，从A岛看B，C两岛的视角∠BAC是度．

查看试题解析
14. 如图， $A B ∥ C D ， B C ∥ E D ， ∠ B = 80 °$ ，则 $∠ D =$ 度．

查看试题解析
15. 如图，已知AB∥DE∥CF ，若∠ABC＝70°，∠CDE＝130°，则∠BCD的度数为．

查看试题解析
16. 一节数学实践课上，老师让同学们用两个大小、形状都相同的三角板画平行线AB、CD ，并要说出自己做法的依据.小奇、小妙两位同学的做法如图：小奇说：“我做法的依据是：同位角相等，两直线平行.”则小妙做法的依据是.

查看试题解析
17. 如图，直线a∥b ，直线c与直线a ， b分别交于点A ， B ．若∠1＝45°，则∠2＝．

查看试题解析
18. 如图，不添加辅助线，请写出一个能判定 $A B / / C D$ 的条件．

查看试题解析
19. 如图，在四边形ABCD中，点E是AB延长线上一点，请添加一个条件，使AB//CD，那么可以添加的条件是（写出一个即可）．

查看试题解析
20. 已知一个角的两边与另一个角的两边分别平行，结合图①②，

(1)、如图①②，则 $A B ∥ E F$ ， $B C ∥ D E$ ，则 $∠ 1$ 与 $∠ 2$ 的数量关系是；

(2)、若两个角的两边互相平行，且一个角比另一个角的2倍少 $30 °$ ，则这两个角的度数分别是．

查看试题解析
21. 如图，下列条件：① $∠ B A D + ∠ A B C = 180 °$ ；② $∠ 1 = ∠ 2$ ；③ $∠ 3 = ∠ 4$ ；④ $∠ B A D = ∠ B C D$ ，能判定 $A D ∥ B C$ 的是（填写正确答案的序号）．

查看试题解析
22. 如图是一块长方形的场地，长AB=a(m)，宽AD=b(m).已知从A，B两处入口的小路宽都为1m，两小路汇合处路宽为2m，其余部分种植草坪，则草坪的面积为m².

查看试题解析

三、综合题

23.

(1)、已知m+4n﹣3＝0，求2^m•16ⁿ的值；

(2)、已知n为正整数，且x²ⁿ＝4，求（x³ⁿ）²﹣2（x²）²ⁿ的值．

查看试题解析
24. 已知 $1 0^{a} = 5$ ， $1 0^{b} = 6$ ，求下列各式的值：

(1)、 $1 0^{a + b}$ ；

(2)、 $1 0^{2 - 2 a + b}$ ．

查看试题解析
25. 比较下列各题中幂的大小：

(1)、比较 $2^{55}$ ， $3^{44}$ ， $5^{33}$ ， $6^{22}$ 这 $4$ 个数的大小关系；

(2)、已知 $a = 8 1^{31}$ ， $b = 2 7^{41}$ ， $c = 9^{61}$ ，比较 $a$ 、 $b$ 、 $c$ 的大小关系；

(3)、已知 $P = \frac{9 9^{9}}{9^{99}}$ ， $Q = \frac{1 1^{9}}{9^{90}}$ ，比较 $P$ ， $Q$ 的大小关系．

查看试题解析
26.

(1)、已知 $a^{m} = 10$ ， $a^{n} = 2$ ，求 $a^{m - 2 n}$ ；

(2)、已知 $2 x + 5 y - 3 = 0$ ，求 $4^{x} \cdot 3 2^{y}$ 的值．

查看试题解析
27. 阅读下列材料，并补充完整，然后解答问题

(1)、试比较 $3^{55} ， 4^{44} ， 5^{33}$ 的大小，并完成填空
解： $3^{55} = {3^{11}}^{\times 5} = (3^{5})^{11} =$ （）¹¹ ，同理： $4^{44} =$ （）¹¹ ， $5^{33} =$ （）¹¹
因为：当底数大于1，指数大于1且相同时，底数越大，幂就越大．所以：＜＜．

(2)、请利用上述解题思路比较 $2^{125} ， 3^{100} ， 4^{75}$ 的大小．

查看试题解析
28. 已知 $10^{m} = 50$ ， $10^{n} = 0.5$ ，求：

(1)、 $m - n$ 的值；

(2)、 $9^{m} \div 3^{2 n}$ 的值

查看试题解析
29. 若 $a^{m} = a^{n}$ （ $a > 0$ 且 $a \neq 1$ ， m、n是正整数），则 $m = n$ ．利用上面结论解决下面的问题：

(1)、如果 $2^{x + 1} \cdot 2^{x} = 2^{5}$ ，求x的值；

(2)、如果 $2^{x + 1} + 2^{x} = 24$ ，求x的值．

查看试题解析
30. 尝试解决下列有关幂的问题：

(1)、若 $9 \times 2 7^{x} = 3^{17}$ ，求 $x$ 的值；

(2)、已知 $a^{x} = - 2$ ， $a^{y} = 3$ ，求 $a^{3 x - 2 y}$ 的值；

查看试题解析
31. 已知 $a^{x} = 3$ ， $a^{y} = 5$ ，求：

(1)、 $a^{x + y}$ 的值；

(2)、 $a^{2 x - y}$ 的值．

查看试题解析
32.

(1)、已知 $1 0^{m} = 2$ ， $1 0^{n} = 3$ ，求 $1 0^{3 m + 2 n + 1}$ 的值；

(2)、已知 $3 m + 2 n - 5 = 0$ ，求 $8^{m} \times 4^{n}$ 的值．

查看试题解析
33.

(1)、若 $2^{m} = 8$ ，则 $m =$ ；若 $2^{n} \cdot 3^{n} = 36$ ，则 $n =$ ；

(2)、若 $2^{x} \cdot 3^{x} \cdot 6^{x} = 3 6^{4 - x}$ ，求x的值．

查看试题解析
34. 阅读下列各式：（ab）²＝a²b² ，（ab）³＝a³b³ ，（ab）⁴＝a⁴b⁴…

(1)、归纳得（ab）n＝；（abc）n＝；

(2)、计算4¹⁰⁰×0.25¹⁰⁰＝；（ $\frac{1}{2}$ ）⁵×3⁵×（ $\frac{2}{3}$ ）⁵＝；

(3)、应用上述结论计算： ${(- 0.125)}^{2017} \times 2^{2018} \times 4^{2016}$ 的值.

查看试题解析
35.

(1)、已知 $a^{m} = 2 ， a^{n} = 3$ ，求 $a^{m - n}$ 的值；

(2)、已知 $3^{m} = 5 ， 3^{n} = 2$ ，求 $3^{3 m + 2 n + 1}$ 的值.

(3)、 $x - 2 y + 1 = 0$ ，求： $2^{x} \div 4^{y} \times 8$ 的值.

查看试题解析
36. 我们规定： $a^{- p} = \frac{1}{a^{p}} (a \neq 0)$ ，即 $a$ 的负 $p$ 次幂等于 $a$ 的 $p$ 次幂的倒数．例： $4^{- 2} = \frac{1}{4^{2}}$ ．

(1)、计算： ${(- 2)}^{- 2} =$ ；若 $2^{- p} = \frac{1}{8}$ ，则 $p =$ ；

(2)、若 $a^{- 2} = \frac{1}{16}$ ，求 $a$ 的值；

(3)、若 $a^{- p} = \frac{1}{9}$ ，且 $a$ ， $p$ 为整数，求满足条件的 $a$ ， $p$ 的值．

查看试题解析