吉林省松原市扶余市2023-2024学年七年级上学期数学期末考试试卷
试卷更新日期:2024-03-12 类型:期末考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. 如图是中国古代数学著作《九章算术》,“方程” 一章中首次正式引入了负数.在生活中,我们规定(↑100 )元表示收入100元,那么(↓80)元表示( )
 A、支出80元 B、收入20元 C、支出20元 D、收入80元2. 将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A、支出80元 B、收入20元 C、支出20元 D、收入80元2. 将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( ) A、
A、 B、
B、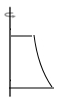 C、
C、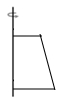 D、
D、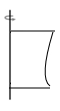 3. 在 , , , , 中,整式有( )A、2个 B、3个 C、4个 D、5个4. 按图中程序运算,如果输入 , 则输出的结果是( )
3. 在 , , , , 中,整式有( )A、2个 B、3个 C、4个 D、5个4. 按图中程序运算,如果输入 , 则输出的结果是( ) A、1 B、3 C、5 D、75. 若x2+xy=A,y2-xy=B,则式子x2-3xy+4y2应表示为( )A、 B、 C、 D、6. 若单项式与的和仍为单项式,则的值为( )A、 B、3 C、4 D、7. 某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是( )A、不盈不亏 B、盈利8元 C、亏损8元 D、亏损15元8. 某射箭运动员在一次比赛中前6次射击共击中52环,如果他要打破89环(10次射击,每次射击最高中10环)的记录,则他第7次射击不能少于( )A、6环 B、7环 C、8环 D、9环9. 把一副三角尺按如图所示的位置摆放,形成了两个角,设这两个角分别是 , . 若 , 则( )
A、1 B、3 C、5 D、75. 若x2+xy=A,y2-xy=B,则式子x2-3xy+4y2应表示为( )A、 B、 C、 D、6. 若单项式与的和仍为单项式,则的值为( )A、 B、3 C、4 D、7. 某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是( )A、不盈不亏 B、盈利8元 C、亏损8元 D、亏损15元8. 某射箭运动员在一次比赛中前6次射击共击中52环,如果他要打破89环(10次射击,每次射击最高中10环)的记录,则他第7次射击不能少于( )A、6环 B、7环 C、8环 D、9环9. 把一副三角尺按如图所示的位置摆放,形成了两个角,设这两个角分别是 , . 若 , 则( ) A、 B、 C、 D、10. 如图,在直线上要找一点C , 且使 , 则点C应( )
A、 B、 C、 D、10. 如图,在直线上要找一点C , 且使 , 则点C应( ) A、在P , Q之间找 B、在点P左边找 C、在点Q右边找 D、在P , Q之间或在点Q右边找
A、在P , Q之间找 B、在点P左边找 C、在点Q右边找 D、在P , Q之间或在点Q右边找二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 如图,两个完全相同的三角形和三角形的顶点C , 重合.若且 , 则 .
 12. 定义一种新运算: , 解决下列问题:(1);(2)当时,的结果为 .13. 我们规定能使等式 成立的一对数(m,n)为“好友数对”.例如当m=2,n=-8 时,能使等式成立,则(2,﹣8)是“好友数对”.若(a,6)是“好友数对”,则a=.14. 若关于x、y的代数式 中不含三次项,则m-6n的值为.15. 有若干个数,第一个数记为 , 第二个数记为 , …,第n个数记为 . 若 , 从第二个数起,每个数都等于“1与它前面那个数的差的倒数”, .
12. 定义一种新运算: , 解决下列问题:(1);(2)当时,的结果为 .13. 我们规定能使等式 成立的一对数(m,n)为“好友数对”.例如当m=2,n=-8 时,能使等式成立,则(2,﹣8)是“好友数对”.若(a,6)是“好友数对”,则a=.14. 若关于x、y的代数式 中不含三次项,则m-6n的值为.15. 有若干个数,第一个数记为 , 第二个数记为 , …,第n个数记为 . 若 , 从第二个数起,每个数都等于“1与它前面那个数的差的倒数”, .三、解答题(本大题共8个小题,共75分)
-
16. 有一个写运算符号的游戏:在“”中的每个内填入“+,-,×,÷”中的某一个(可重复使用),然后计算结果.(1)、请计算琪琪填入符号后得到的算式:;(2)、嘉嘉填入符号后得到的算式是 , 一不小心擦掉了里的运算符号,但她知道结果是 , 请推算内的符号.17. 小王在解关于x的方程2﹣=3a﹣2x时,误将﹣2x看作+2x,得方程的解x=1.(1)、求a的值;(2)、求此方程正确的解.18. 化简求值: ,其中x,y满足 与 是同类项.19. 已知方程 的解与关于的方程 的解互为相反数,求a的值.20. 如图, , , 若 , 求的大小.
 21. 某单位组织70名职工组团前往某旅游景点,该景点规定:①门票60元/人,无优惠;②上山可坐景点观光车,观光车有四座车和九座车,已知游客坐四座车比坐九座车每人每趟多花费5元;满载时,一辆九座车每趟的收入比一辆四座车多30元.(1)、游客坐四座车和九座车每人每趟的费用分别是多少元?(2)、若这些职工正好坐满每辆车且总费用为4980元,则这个单位租用的四座车和九座车各多少辆?22. 如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
21. 某单位组织70名职工组团前往某旅游景点,该景点规定:①门票60元/人,无优惠;②上山可坐景点观光车,观光车有四座车和九座车,已知游客坐四座车比坐九座车每人每趟多花费5元;满载时,一辆九座车每趟的收入比一辆四座车多30元.(1)、游客坐四座车和九座车每人每趟的费用分别是多少元?(2)、若这些职工正好坐满每辆车且总费用为4980元,则这个单位租用的四座车和九座车各多少辆?22. 如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC. (1)、若∠AOC=30°,求∠DOE的度数;(2)、若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);(3)、在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.23. 如图1,点C在线段上,图中共有三条线段和 , 若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段的“巧点”.
(1)、若∠AOC=30°,求∠DOE的度数;(2)、若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);(3)、在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.23. 如图1,点C在线段上,图中共有三条线段和 , 若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段的“巧点”. (1)、线段的中点 这条线段的“巧点”;(填“是”或“不是”)(2)、若 , 点C是线段AB的巧点,则;(3)、如图2,已知 , 动点P从点A出发,以 的速度沿向点B匀速移动;点Q从点B出发,以的速度沿向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为 . 当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?并说明理由.
(1)、线段的中点 这条线段的“巧点”;(填“是”或“不是”)(2)、若 , 点C是线段AB的巧点,则;(3)、如图2,已知 , 动点P从点A出发,以 的速度沿向点B匀速移动;点Q从点B出发,以的速度沿向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为 . 当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?并说明理由.