吉林省长春市南关区2023-2024学年七年级上学期数学期末考试试题
试卷更新日期:2024-03-12 类型:期末考试
一、选择题(本大题共有8道小题,每小题3分,共24分)
-
1. 如图,在数轴上对应的数互为相反数的两个点是( )
 A、点A和点C B、点B和点C C、点A和点B D、点B和点D2. 杭州第19届亚运会公众售票官方网站8日上午上线开放注册,首批上架比赛项目包括举重、克柔术、网球、花样游泳、击剑、摔跤、蹦床、高尔夫球、跳水、游泳、软式网球、攀岩等12个项目,总计预售113700张门票,数据113700用科学记数法可表示为( )A、 B、 C、 D、3. 下列四个生活中的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要确定两棵树的位置,就能确定这一行树所在的直线;③从地到地架设电线,总是尽可能沿着线段方向架设;④把弯曲的公路改直,就能缩短路程.其中可以用基本事实“两点确定一条直线”来解释的有( )A、①② B、①③ C、②③ D、③④4. 如图,图(1)和图(2)中所有的正方形都完全相同,将图(1)的正方形放在图(2)中的某一位置,其中所组成的图形不能围成正方体的是( )
A、点A和点C B、点B和点C C、点A和点B D、点B和点D2. 杭州第19届亚运会公众售票官方网站8日上午上线开放注册,首批上架比赛项目包括举重、克柔术、网球、花样游泳、击剑、摔跤、蹦床、高尔夫球、跳水、游泳、软式网球、攀岩等12个项目,总计预售113700张门票,数据113700用科学记数法可表示为( )A、 B、 C、 D、3. 下列四个生活中的现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要确定两棵树的位置,就能确定这一行树所在的直线;③从地到地架设电线,总是尽可能沿着线段方向架设;④把弯曲的公路改直,就能缩短路程.其中可以用基本事实“两点确定一条直线”来解释的有( )A、①② B、①③ C、②③ D、③④4. 如图,图(1)和图(2)中所有的正方形都完全相同,将图(1)的正方形放在图(2)中的某一位置,其中所组成的图形不能围成正方体的是( )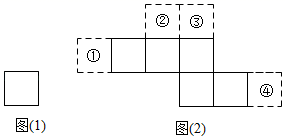 A、① B、② C、③ D、④5. 若单项式与是同类项,则的值是( )A、0 B、1 C、 D、20236. “盈不足问题”作为我国数学的古典问题,在2000多年前的《九章算术》一书中就有很详尽而深刻的阐述.书中记载:今有人买鸡,人出九,盈十一;人出六,不足十六.问人数、物价各几何?意思是:有若干人一起买鸡,如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.买鸡的人数、鸡的价钱各是多少?若设有x个人共同买鸡,根据题意列一元一次方程,正确的是( )
A、① B、② C、③ D、④5. 若单项式与是同类项,则的值是( )A、0 B、1 C、 D、20236. “盈不足问题”作为我国数学的古典问题,在2000多年前的《九章算术》一书中就有很详尽而深刻的阐述.书中记载:今有人买鸡,人出九,盈十一;人出六,不足十六.问人数、物价各几何?意思是:有若干人一起买鸡,如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.买鸡的人数、鸡的价钱各是多少?若设有x个人共同买鸡,根据题意列一元一次方程,正确的是( ) A、 B、 C、 D、7. 如图,直线、相交于点 , , , 则的度数是( ).
A、 B、 C、 D、7. 如图,直线、相交于点 , , , 则的度数是( ). A、 B、 C、 D、8. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A、 B、 C、 D、8. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
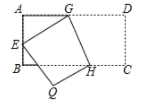 A、112° B、110° C、108° D、106°
A、112° B、110° C、108° D、106°二、填空题(本大题共有6道小题,每小题3分,共18分)
-
9. 比较大小:(用“>”“<”或“=”填空).10. 近似数万精确到位.11. 如图,一把长方形直尺沿直线断开并错位摆放,点、、、在同一条直线上,若 , 则的度数为 .
 12. 计算:°.13. 若 , 则的值为 .14. 如图所示,未来公园的广场背景墙上有一系列用灰砖和白砖铺成的图案,图①有1块灰砖,8块白砖;图②有4块灰砖,12块白砖;以此类推.若某个图案中有49块灰砖,则此图案中有块白砖.
12. 计算:°.13. 若 , 则的值为 .14. 如图所示,未来公园的广场背景墙上有一系列用灰砖和白砖铺成的图案,图①有1块灰砖,8块白砖;图②有4块灰砖,12块白砖;以此类推.若某个图案中有49块灰砖,则此图案中有块白砖.
三、解答题(本大题共有10道小题,共78分)
-
15. 计算:(1)、;(2)、;(3)、 .16. 解方程:(1)、;(2)、;(3)、 .17. 先化简,再求值 , 其中 .18. 在2023年空军航空开放活动·长春航空展中,“红鹰”飞行表演队进行了飞行表演,某飞机起飞5千米后的高度变化情况如下表所示,按要求解答下列问题:
高度变化
上升3.6千米
下降2.1千米
上升1.4千米
下降3.9千米
记作
(1)、表格中“下降3.9千米”记作:km;(2)、请通过计算说明该飞机完成上述4个表演动作后,离地面的高度是多少千米;(3)、如果飞机每上升1千米需消耗6升燃油,每下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油.19. 如图是6×6的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段、的端点均在格点上,请按要求画图,并回答问题(要求:作图只用无刻度的直尺) (1)、过点作直线的垂线,垂足为点 , 并直接写出点到直线的距离: ;(2)、作线段 . 且;(3)、若点在线段上,连结、 , 当的长度最小时,在图中画出点 , 并说明此时的长度最小的理由: .20. 已知线段 , 延长到C , 使 , D为的中点,若cm,求的长.
(1)、过点作直线的垂线,垂足为点 , 并直接写出点到直线的距离: ;(2)、作线段 . 且;(3)、若点在线段上,连结、 , 当的长度最小时,在图中画出点 , 并说明此时的长度最小的理由: .20. 已知线段 , 延长到C , 使 , D为的中点,若cm,求的长.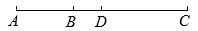 21. 已知,如图,点A , , 在同一条直线上,平分 , .
21. 已知,如图,点A , , 在同一条直线上,平分 , . (1)、求证:是的平分线,将下列证明过程补充完整(其中括号里填写推理依据)
(1)、求证:是的平分线,将下列证明过程补充完整(其中括号里填写推理依据)证明:∵ ,
∴ ▲ , ,
又∵平分 ,
∴ ▲ .( )
∴ ▲ .( )
∴是的平分线.
(2)、图中的补角是 .22. 随着《某市生活垃圾分类管理条例》正式实施,某市垃圾分类工作进入强制实施阶段,某小区物业管理负责人提出了购买分类垃圾桶的方案.方案一:买A型号分类垃圾桶,需要费用2500元,以后每月的垃圾处理费用为300元;
方案二:买B型号分类垃圾桶,需要费用1500元,以后每月的垃圾处理费用为400元;设缴费时长为x个月,方案一和方案二的购买费和垃圾处理费的和分别为M元、N元.
(1)、 , (分别用含x的式子表示).(2)、若缴费时长为12个月,则哪种方案的费用更少?并说明理由.(3)、当缴费时长为多少个月时,两种方案的费用相同?23. (1)、【感知】如图①,若 , 平分 , 求证: .
(1)、【感知】如图①,若 , 平分 , 求证: .请将下列证明过程补充完整:
证明:∵平分 , (已知),
∴ ▲ (角平分线的定义),
∵(已知),∴ ▲ (两直线平行,内错角相等)
∴(等量代换).
(2)、【探索】如图②,平分 , , 点在射线上,点在线段上,若 , 求证: .(3)、【拓展】如图③,将【探索】中的点移动到线段的延长线上,其他条件不变,若 , 请直接写出的度数.24. 已知数轴上A , , 三个点表示的数分别是 , , , 且满足 , 动点从点A出发,以每秒2个单位长度的速度沿数轴向终点运动,点运动时间为t秒. (1)、 , ;(2)、点在数轴上表示的数为(用含的代数式表示);(3)、另一动点也从点A出发,沿数轴运动至点后,立刻以原来的速度返回到A点停止,
(1)、 , ;(2)、点在数轴上表示的数为(用含的代数式表示);(3)、另一动点也从点A出发,沿数轴运动至点后,立刻以原来的速度返回到A点停止,①若、两点同时出发,点的速度为每秒4个单位长度,当时,求的值;
②若点运动到点时,点再从点A出发,当时, , 请直接写出点的运动速度.