吉林省松原市前郭县南部学区2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-03-12 类型:期末考试
一、选择题(每小题2分,共12分)
-
1. 若分式 有意义,则x的取值范围是( )A、 B、 C、 D、2. 下面所给的银行标志图中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算中,正确的是( )A、 B、 C、 D、4. 经测算,一粒芝麻的质量约为 , 数据用科学记数法表示为( )A、 B、 C、 D、5. 小华在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为 , 则中间一项的系数是( )A、6 B、 C、6或 D、186. 如图,在中, 点M,点N为AC边上的两点, , , ND⊥BC于点D,且 , 若 , 则( )
3. 下列运算中,正确的是( )A、 B、 C、 D、4. 经测算,一粒芝麻的质量约为 , 数据用科学记数法表示为( )A、 B、 C、 D、5. 小华在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为 , 则中间一项的系数是( )A、6 B、 C、6或 D、186. 如图,在中, 点M,点N为AC边上的两点, , , ND⊥BC于点D,且 , 若 , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共24分)
-
7. 计算: .8. 若分式的值为零,则x的值为 .9. 分解因式:.10. 已知一个n边形的内角和是其外角和的5倍,则n= .11. 如图所示, , 则
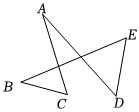 12. 如图所示, , 表示两根长度相同的木条,若是 , 的中点,经测量 , 则容器的内径为 .
12. 如图所示, , 表示两根长度相同的木条,若是 , 的中点,经测量 , 则容器的内径为 . 13. 如图,在中, , 点E在的垂直平分线上,平分 . 若 , , 则 .
13. 如图,在中, , 点E在的垂直平分线上,平分 . 若 , , 则 . 14. 如图,在中,平分 , , 于点E , 若 , , , 则四边形的面积是 .
14. 如图,在中,平分 , , 于点E , 若 , , , 则四边形的面积是 .
三、解答题(每小题5分,共20分)
-
15. 解方程:16. 如图,已知中, , , E是的中点, , 连接 . 求证:是等边三角形.
 17. 先化简,再求值: , 其中 , .18. 已知:P是线段AB的中点,∠1=∠2,PD=PC,求证:∠C=∠D
17. 先化简,再求值: , 其中 , .18. 已知:P是线段AB的中点,∠1=∠2,PD=PC,求证:∠C=∠D
四、解答题(每小题7分,共28分)
-
19. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点.线段的端点A、B均在格点上,分别按下列要求画图.
 (1)、在图①中画一个 , 使的面积是10;(2)、在图②中画一个 , 使是轴对称图形;(3)、在图③中画一个 , 点E在格点上,且大于 .20. 先化简: , 再从1、2、0中选择一个合适的数代入求值.21. 已知.三角形的底边长为(2x+1)cm,高是(x﹣2)cm,若把底边和高各增加5厘米,那么三角形面积增加了多少?并求出x=3时三角形增加的面积.22. 如图,在四边形中,对角线平分 , , 与的延长线交于点E .
(1)、在图①中画一个 , 使的面积是10;(2)、在图②中画一个 , 使是轴对称图形;(3)、在图③中画一个 , 点E在格点上,且大于 .20. 先化简: , 再从1、2、0中选择一个合适的数代入求值.21. 已知.三角形的底边长为(2x+1)cm,高是(x﹣2)cm,若把底边和高各增加5厘米,那么三角形面积增加了多少?并求出x=3时三角形增加的面积.22. 如图,在四边形中,对角线平分 , , 与的延长线交于点E . (1)、求证:;(2)、若 , 直接写出图中所有的锐角等腰三角形.
(1)、求证:;(2)、若 , 直接写出图中所有的锐角等腰三角形.五、解答题(每小题8分,共16分)
-
23. 某中学为了止学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动,市场上每捆A种菜苗的价格是菜苗基地的倍,用300元在市场上购买的A种菜苗比在菜苗基地购买的少5捆.(1)、求菜苗基地每捆A种菜苗的价格;(2)、菜苗基地每捆B种菜苗的价格是30元,学校决定在菜苗基地购买A、B两种菜苗共100捆,所花的费用不超过2400元,则应购买A种菜苗至少多少捆?24.
 (1)、【问题】如图①,在等边中,点D、E在、上,若CD=AE,、交于点O , 则度;(2)、【探究】如图②,在等边中,点D、E分别在、的延长线上,求的度数;(3)、【应用】如图③,在中, , 点D、E分别在、的延长线上,若 , , 则度.
(1)、【问题】如图①,在等边中,点D、E在、上,若CD=AE,、交于点O , 则度;(2)、【探究】如图②,在等边中,点D、E分别在、的延长线上,求的度数;(3)、【应用】如图③,在中, , 点D、E分别在、的延长线上,若 , , 则度.六、解答题(每小题10分,共20分)
-
25.
 (1)、【教材原题】观察图①,用等式表示下图中图形的面积的运算为 .(2)、【类比探究】观察图②,用等式表示图中阴影部分图形的面积和为 .(3)、【应用】a.根据图②所得的公式,若 , , 则 .
(1)、【教材原题】观察图①,用等式表示下图中图形的面积的运算为 .(2)、【类比探究】观察图②,用等式表示图中阴影部分图形的面积和为 .(3)、【应用】a.根据图②所得的公式,若 , , 则 .b.若x满足 , 求的值.
(4)、【拓展】如图③,某学校有一块梯形空地 , 于点E , , . 该校计划在和区域内种花,在和的区域内种草.经测量种花区域的面积和为 , , 直接写出种草区域的面积和.26. 如图,是等腰直角三角形, , , 于点 . 点为边上一动点,连接 , 作 , 使点在射线上,过点作于点 . (1)、的长为;(2)、当点在线段上时,求证:;(3)、若将分成面积比为的两部分,求的长;(4)、若的一个内角为 , 直接写出的大小.
(1)、的长为;(2)、当点在线段上时,求证:;(3)、若将分成面积比为的两部分,求的长;(4)、若的一个内角为 , 直接写出的大小.