备战2024年中考数学细点逐一突破真题训练第7章一次函数
试卷更新日期:2024-03-12 类型:一轮复习
一、函数的基本概念
-
1. 关于函数 , 给出下列说法正确的是:( )
①当时,该函数是一次函数;
②若点在该函数图象上,且 , 则;
③若该函数不经过第四象限,则;
④该函数恒过定点 .
A、①②④ B、①③④ C、②③④ D、①②③2. 下列不能表示是的函数的是( )A、
B、x 0 5 10 15 y 3 3.5 4 4.5  C、
C、 D、
3. 函数y=的自变量x的取值范围为 .
D、
3. 函数y=的自变量x的取值范围为 .二、一次函数的图像性质
-
4. 下表中给出的是一个一次函数的自变量与函数的几组对应值:
…
…
…
0
…
下列各选项中,正确的是( )
A、y随x的增大而增大 B、该函数的图象经过点 C、该函数的图象不经过第四象限 D、该函数图象与坐标轴围成的三角形的面积为165. 直线y=﹣ax+a与直线y=ax在同一坐标系中的大致图象可能是( )A、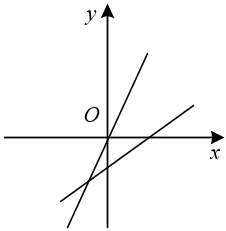 B、
B、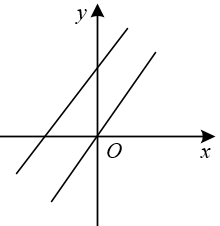 C、
C、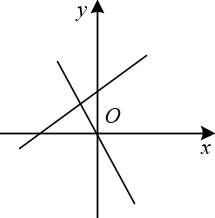 D、
D、 6. 已知二次函数的图象如图所示,则一次函数的图象大致为( )
6. 已知二次函数的图象如图所示,则一次函数的图象大致为( )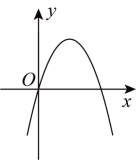 A、
A、 B、
B、 C、
C、 D、
D、
三、一次函数与方程(组)
-
7. 已知方程的解为 , 则一次函数的图像与轴交点的横坐标为( )A、3 B、 C、 D、8. 函数和的图象相交于点 , 则方程的解为 .
 9. 已知一次函数的图象经过点 , 且当时, . 则下列结论正确的是( ).A、a , c都为正,且 B、a , c都为正,且 C、a , c至少有一项为正,且 D、a , c至少有一项为正,且10. 如图,已知直线与轴交于点 , 且和直线交于点 , 根据以上信息解答下列问题:
9. 已知一次函数的图象经过点 , 且当时, . 则下列结论正确的是( ).A、a , c都为正,且 B、a , c都为正,且 C、a , c至少有一项为正,且 D、a , c至少有一项为正,且10. 如图,已知直线与轴交于点 , 且和直线交于点 , 根据以上信息解答下列问题: (1)、求的值.(2)、不解关于x,y的方程组请你直接写出它的解.(3)、若直线表示的两个一次函数值都大于0时,恰好 , 求直线的函数表达式.11. 在平面直角坐标系中,一次函数y=3x﹣1与y=ax(a≠0)的图象的交点坐标是(1,2),则方程组的解是 .12. 已知二元一次方程组的解为 , 则在同一平面直角坐标系中,直线:与直线:的交点坐标为( )A、 B、 C、 D、
(1)、求的值.(2)、不解关于x,y的方程组请你直接写出它的解.(3)、若直线表示的两个一次函数值都大于0时,恰好 , 求直线的函数表达式.11. 在平面直角坐标系中,一次函数y=3x﹣1与y=ax(a≠0)的图象的交点坐标是(1,2),则方程组的解是 .12. 已知二元一次方程组的解为 , 则在同一平面直角坐标系中,直线:与直线:的交点坐标为( )A、 B、 C、 D、四、一次函数与一元一次不等式
-
13. 已知是一次函数图象上的不同的两个点,若 , 则k的取值范围是( )A、 B、 C、 D、14. 如图所示,已知 , 是一次函数图象与反比例函数图象的两个交点.
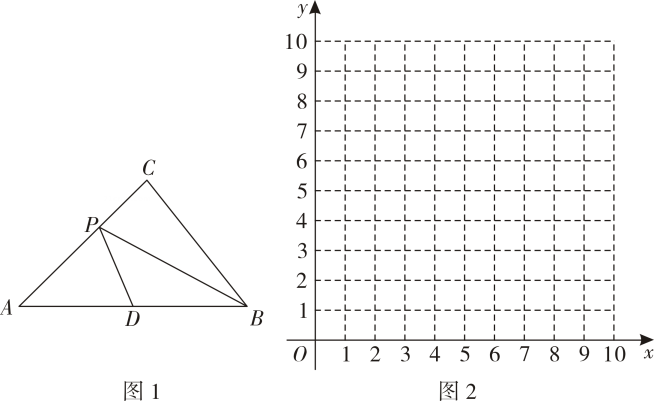
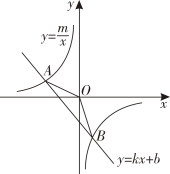 (1)、求反比例函数和一次函数的表达式;(2)、观察图象,当取何值时, .15. 一次函数的图象与反比例函数的图象交于点和点 , 与轴交于点 .
(1)、求反比例函数和一次函数的表达式;(2)、观察图象,当取何值时, .15. 一次函数的图象与反比例函数的图象交于点和点 , 与轴交于点 . (1)、求反比例函数和一次函数的解析式,并在网格中画出一次函数的图象.(2)、根据图象,直接写出关于的不等式的解集.(3)、点在一次函数的图象上,过点作轴于点 , 交反比例函数的图象于点 , 连接 , , 求四边形的面积.
(1)、求反比例函数和一次函数的解析式,并在网格中画出一次函数的图象.(2)、根据图象,直接写出关于的不等式的解集.(3)、点在一次函数的图象上,过点作轴于点 , 交反比例函数的图象于点 , 连接 , , 求四边形的面积.五、一次函数的应用
-
16. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,图中的折线表示两车相距的距离(千米)与慢车行驶的时间x(小时)之间的函数关系.根据图象进行以下探究:
 (1)、甲、乙两地之间相距的路程为 千米;图中点B的实际意义为 ;(2)、求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围;(3)、当两车之间的距离不小于800千米时,直接写出x的取值范围.17. 如图,直线L1: 与 轴, 轴分别交于A,B两点,点P( ,3)为直线AB上一点,另一直线L2: 经过点P.
(1)、甲、乙两地之间相距的路程为 千米;图中点B的实际意义为 ;(2)、求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围;(3)、当两车之间的距离不小于800千米时,直接写出x的取值范围.17. 如图,直线L1: 与 轴, 轴分别交于A,B两点,点P( ,3)为直线AB上一点,另一直线L2: 经过点P. (1)、求点A、B坐标;(2)、求点P坐标和 的值;(3)、若点C是直线L2与 轴的交点,点Q是 轴上一点,当△CPQ的面积等于3时,求出点Q的坐标18. 某文具店自疫情以来网络销量不断增大,为了节省快递费用,与快递公司协商后
(1)、求点A、B坐标;(2)、求点P坐标和 的值;(3)、若点C是直线L2与 轴的交点,点Q是 轴上一点,当△CPQ的面积等于3时,求出点Q的坐标18. 某文具店自疫情以来网络销量不断增大,为了节省快递费用,与快递公司协商后
达成协议,协议部分内容如下:同城快递发货费用每件价格固定,但低于外市快递每件发货价格.
外市快递每日发货不超过件时,发货价格按每件元计算,超过件时超过的部分每件发货价格有一定的优惠.
注:文具店单件货品不超过标准重量,外市快递不包含偏远地区文具店每日同城快递和外市快递各自发货所花金额元与各自发货件数件之间的函数关系如图所示:
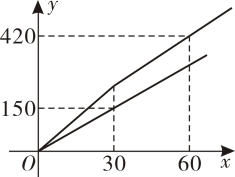 (1)、求同城快递每件发货价格.
(1)、求同城快递每件发货价格.
(2)、求外市快递发货费用与外市发货件数的函数关系式.
(3)、文具店某日发货件同城和外市均有销量 , 共花费元,求这一天文具店同城快递发货件数.19. 富民县今年种植的杨梅喜获丰收,杨梅上市的成本价为元 , 售价为元 , 该农户对杨梅一个月(天)的销售情况进行记录,然后将日销量y(单位:)与销售时间x(单位:天)之间的函数关系绘成如图所示的图象.图中线段表示的函数关系中,时间每增加1天,日销量减少 . (1)、请直接写出该农户第天的日销量和这天的销售利润;(2)、求y与x之间的函数关系式,并写出x的取值范围;(3)、求销售期间日销售最大利润是多少元?20. 为进一步落实“乡村振兴”工程,某村在政府的扶持下建起了大棚基地,准备种植两种蔬菜.若种植亩种蔬菜和亩种蔬菜,总收入为万元;若种植亩种蔬菜和亩种蔬菜,总收入为万元.(1)、求种植两种蔬菜,平均每亩收入各是多少万元?(2)、村里规划种植这两种蔬菜共亩,且种蔬菜的种植面积不少于种蔬菜种植面积的倍,问种蔬菜种植多少亩,总收入最大,最大总收入是多少?
(1)、请直接写出该农户第天的日销量和这天的销售利润;(2)、求y与x之间的函数关系式,并写出x的取值范围;(3)、求销售期间日销售最大利润是多少元?20. 为进一步落实“乡村振兴”工程,某村在政府的扶持下建起了大棚基地,准备种植两种蔬菜.若种植亩种蔬菜和亩种蔬菜,总收入为万元;若种植亩种蔬菜和亩种蔬菜,总收入为万元.(1)、求种植两种蔬菜,平均每亩收入各是多少万元?(2)、村里规划种植这两种蔬菜共亩,且种蔬菜的种植面积不少于种蔬菜种植面积的倍,问种蔬菜种植多少亩,总收入最大,最大总收入是多少?六、分析函数图像