备战2024年中考数学细点逐一突破真题训练第6章平面直角坐标系与函数,几何相关
试卷更新日期:2024-03-12 类型:一轮复习
一、象限内坐标点特征
-
1. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若点与点关于y轴对称,则的值是( )A、 B、 C、1 D、23. 以方程组的解为坐标的点在平面直角坐标系中的位置是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 在平面直角坐标系中,若点与点关于原点对称,则的值是 .5. 若实数 , 分别满足下列条件:
;(2) . 试判断点所在的象限
6. 已知 ,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )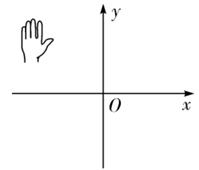 A、 B、 C、 D、7. 已知点是平面直角坐标系中的点.(1)、若点A在第二象限的角平分线上,求a的值;(2)、若点A在第三象限,且到两坐标轴的距离和为9,请确定点A的坐标.
A、 B、 C、 D、7. 已知点是平面直角坐标系中的点.(1)、若点A在第二象限的角平分线上,求a的值;(2)、若点A在第三象限,且到两坐标轴的距离和为9,请确定点A的坐标.二、规律探索类坐标点
-
8. 如图,是正三角形,点A在第一象限,点、 . 将线段 绕点C按顺时针方向旋转至;将线段绕点B按顺时针方向旋转至;将线段绕点A按顺时针方向旋转至;将线段绕点C按顺时针方向旋转至;……以此类推,则点的坐标是 .
 9. 已知,都是边长为2的等边三角形,按下图所示摆放.点都在x轴正半轴上,且 , 则点的坐标是 .
9. 已知,都是边长为2的等边三角形,按下图所示摆放.点都在x轴正半轴上,且 , 则点的坐标是 . 10. 如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P为位似中心作正方形 , 正方形 , 按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为 , , 则顶点的坐标为( )
10. 如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P为位似中心作正方形 , 正方形 , 按此规律作下去,所作正方形的顶点均在格点上,其中正方形的顶点坐标分别为 , , 则顶点的坐标为( )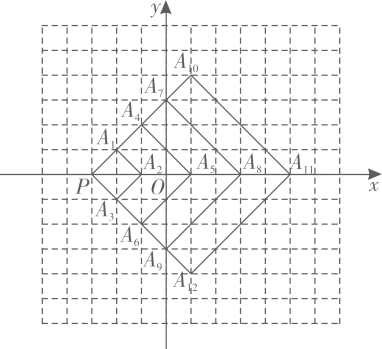 A、 B、 C、 D、
A、 B、 C、 D、三、图形变化相关(相似,圆,解直角三角形等)
-
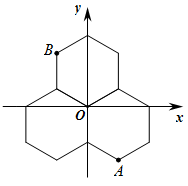
11. 三个能够重合的正六边形的位置如图.已知B点的坐标是 , 则A点的坐标是 .
 12. 如图,在平面直角坐标系中,菱形的边长为 , 点在轴的正半轴上,且 , 将菱形绕原点逆时针方向旋转 , 得到四边形点与点重合 , 则点的坐标是( )
12. 如图,在平面直角坐标系中,菱形的边长为 , 点在轴的正半轴上,且 , 将菱形绕原点逆时针方向旋转 , 得到四边形点与点重合 , 则点的坐标是( )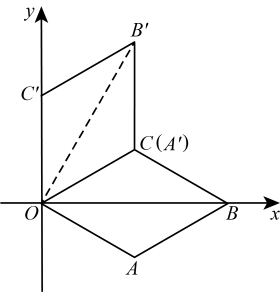 A、 B、 C、 D、13. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)
A、 B、 C、 D、13. 如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点 , 点 , .则点的坐标为.(结果用含a,b的式子表示)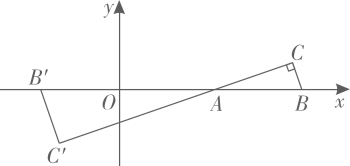 14. 如图,正方形的中心与坐标原点O重合,将顶点绕点逆时针旋转得点 , 再将绕点逆时针旋转得点 , 再将绕点C逆时针旋转得点 , 再将绕点D逆时针旋转得点 , 再将绕点A逆时针旋转得点……依此类推,则点的坐标是.
14. 如图,正方形的中心与坐标原点O重合,将顶点绕点逆时针旋转得点 , 再将绕点逆时针旋转得点 , 再将绕点C逆时针旋转得点 , 再将绕点D逆时针旋转得点 , 再将绕点A逆时针旋转得点……依此类推,则点的坐标是. 15. 如图,在平面直角坐标系中, , , , 经过 , , 三点.
15. 如图,在平面直角坐标系中, , , , 经过 , , 三点. (1)、点的坐标为 .(2)、判断点与的位置关系.
(1)、点的坐标为 .(2)、判断点与的位置关系.四、函数相关(一次函数,反比例函数)
-
16. 在平面直角坐标系中,直线为常数与轴交于点 , 将该直线沿轴向左平移个单位长度后,与轴交于点若点与关于原点对称,则的值为( )A、 B、 C、 D、17. 已知点在同一个函数图象上,则这个函数图象可能是( )A、
 B、
B、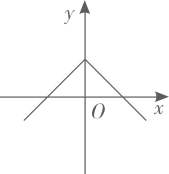 C、
C、 D、
D、 18. 已知抛物线开口向下,且经过第三象限的点 , 若点与原点在抛物线对称轴的异侧,则一次函数的图像不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
18. 已知抛物线开口向下,且经过第三象限的点 , 若点与原点在抛物线对称轴的异侧,则一次函数的图像不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限五、网格作图相关(位似,旋转,平移。轴对称等)
-
19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣4,0),C(﹣2,2),将△ABC绕原点O顺时针旋转90°后得到△A1B1C1 .
 (1)、请写出A1、B1、C1三点的坐标:
(1)、请写出A1、B1、C1三点的坐标:A1 , B1 , C1;
(2)、求点B旋转到点B1的弧长.20. 如图,在直角坐标系中,各点坐标分别为 , , . 先作关于x轴成轴对称的 , 再把平移后得到 . 若 , 则点坐标为( ) A、 B、 C、 D、21. 如图,由边长为1的小正方形组成的网格中建立平面直角坐标系 , 的顶点均在网格线的交点上.
A、 B、 C、 D、21. 如图,由边长为1的小正方形组成的网格中建立平面直角坐标系 , 的顶点均在网格线的交点上. (1)、画出关于点B中心对称的(点A、C的对应点分别是点D、E)(2)、将平移,使点A平移到点处.
(1)、画出关于点B中心对称的(点A、C的对应点分别是点D、E)(2)、将平移,使点A平移到点处.①请画出平移后的(点A、B、C的对应点分别是点、、)
②若点为内一点,则平移后,点P的对应点的坐标为 ▲ (用含、的代数式表示).
22. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , 请按下列要求画图: (1)、将先向右平移4个单位长度、再向下平移5个单位长度,得到 , 画出 , 并写出点的坐标;(2)、以点A为位似中心将放大2倍,得到 , 画出并写出点B2的坐标.23. 如图,在平面直角坐标系中,每个小正方形的边长均为1,的顶点均在网格格点上,且 , , .
(1)、将先向右平移4个单位长度、再向下平移5个单位长度,得到 , 画出 , 并写出点的坐标;(2)、以点A为位似中心将放大2倍,得到 , 画出并写出点B2的坐标.23. 如图,在平面直角坐标系中,每个小正方形的边长均为1,的顶点均在网格格点上,且 , , .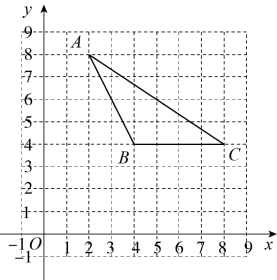 (1)、以原点O为位似中心,在第一象限画出 , 使得与位似,且与的相似比 , 点A、B、C的对应点分别为点、、;(2)、点的坐标为 .
(1)、以原点O为位似中心,在第一象限画出 , 使得与位似,且与的相似比 , 点A、B、C的对应点分别为点、、;(2)、点的坐标为 .六、概率相关
-
24. 在平面直角坐标系中有五个点,分别是 , , , , , 从中任选一个点恰好在第一象限的概率是 .