2024学年沪科版七年级下册第7章一元一次不等式(组)含参问题(培优篇)
试卷更新日期:2024-03-12 类型:同步测试
一、选择题
-
1. 若不等式组有解,则的取值范围是( )A、 B、 C、 D、2. 已知关于的不等式组的最小整数解是2,则实数的取值范围是( )A、 B、 C、 D、3. 若 , 且 , 当时,关于x的代数式恰好能取到两个非负整数值,则a的取值范围是( )A、 B、 C、 D、4. 已知关于的不等式只有2个正整数解,则的取值范围是( )A、 B、 C、 D、5. 若关于x的不等式组有四个整数解,则a的取值范围是( )A、 B、 C、 D、6. 不等式组的所有整数解的和为9,则整数a的值有( )A、1个 B、2个 C、3个 D、4个7. 若关于x的一元一次方程有整数解,且关于y的不等式组有且只有三个整数解,则满足所有条件的整数m的和是( )A、 B、 C、 D、8. 若关于x的一元一次不等式组的解集为 , 且关于x的方程的解为正整数,则符合条件的整数的个数有( )A、2个 B、3个 C、4个 D、5个9. 关于x,y的方程组的解中x与y的差不小于5,则k的取值范围为( )A、 B、 C、 D、10. 运行程序如图所示,从“输入实数 x”到“结果是否<18”为一次程序操作,若输入 x 后程序操作仅进行了三次就停止,那么 x 的取值范围是( )
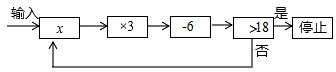 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若不等式组无解,则a的取值范围是 .12. 若关于的不等式组的所存整数解的和为14,则整数的值为.13. 已知关于x , y的方程组的解满足 , 且关于x的不等式组无解,那么所有符合条件的整数a的和为 .14. 对于三个数a , b , c , 我们规定表示这三个数中最大的数.例如 , 若 , 则x的取值范围是 .
三、新定义问题
-
15. 在实数范围内定义一种新运算“★”其运算规则为 , .(1)、若 , 则 .(2)、求不等式的负整数解.16. 定义:对于任何有理数x,符号表示不大于x的最大整数,即 , 例如: , , .(1)、填空: , .(2)、如果 , 求满足条件的x的取值范围;(3)、若 , 求x的值.
四、实践探究题
-
17. 定义:若一元一次方程的解在一元一次不等式的解集范围内,则称一元一次方程为一元一次不等式的“伴随方程”.如:一元一次方程的解为 , 而一元一次不等式的解集为 , 不难发现在范围内,则一元一次方程是一元一次不等式的“伴随方程”(1)、在① , ② , ③三个一元一次方程中,是一元一次不等式的“伴随方程”的有(填序号);(2)、若关于x的一元一次方程是关于x一元一次不等式的“伴随方程”,且一元一次方程不是关于x的一元一次不等式的“伴随方程”.
①求a的取值范围;
②直接写出代数式的最大值.
18. 新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:方程x-1=3的解为x=4,而不等式组的解集为2<x<5,不难发现x=4在2<x<5的范围内,所以方程x-1=3是不等式组的“关联方程”.(1)、在方程①2(x+1)-x=-3;②-1=x;③2x-7=0中,不等式组的“关联方程”是(填序号)(2)、关于x的方程2x-k=6是不等式组的“关联方程”,求k的取值范围;(3)、若关于x的方程-3m=0是关于x的不等式组的“关联方程”,且此时不等式组有3个整数解,试求m的取值范围.19. 我们约定:给定两个不等式组P和Q,若不等式组P的任意一个解,都是不等式组Q的一个解,则称不等式组P为不等式组Q的“子集”.例如:不等式组是的“子集”.
(1)、若不等式组: , , 则其中不等式组是不等式组的“子集”(填A或B);(2)、若关于x的不等式组不是不等式组的“子集”,则a的取值范围是;(3)、若关于x的不等式组有解且是不等式组的“子集”,求a的取值范围;(4)、若关于x的不等式组是不等式组的“子集”且不等式组M的所有整数解的和为15,请求出m,n的取值范围.