吉林省白山市临江市2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-03-11 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 用配方法解方程 , 经过配方可转化为( )A、 B、 C、 D、2. 某小型企业一月份的营业额为200万元,月平均增长率相同,第一季度的总营业额为1000万元.设月平均增长率为 , 可列方程为( )A、 B、 C、 D、3. 下列各组图形中,一定相似的是( )A、两个正方形 B、两个矩形 C、两个菱形 D、两个平行四边形4. 如果在同一盏路灯下,小明与小强的影子一样长,下列说法正确的是( )A、小明比小强的个子高 B、小强比小明的个子高 C、两个人的个子一样高 D、无法判断谁的个子高5. 下列说法中,不正确的是( )A、有一个角是直角的平行四边形是正方形 B、对角线相等的平行四边形是矩形 C、对角线互相平分且垂直的四边形是菱形 D、对边分别相等的四边形是平行四边形6. 如图的几何体是由四个大小相同的正方体组成的,它的俯视图是( )
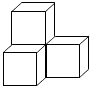 A、
A、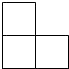 B、
B、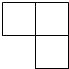 C、
C、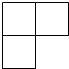 D、
D、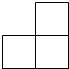 7. 已知点 , , 都在反比例函数的图象上,则( )A、 B、 C、 D、8. 函数和 , 在同一直角坐标系中的大致图象可能是( )A、
7. 已知点 , , 都在反比例函数的图象上,则( )A、 B、 C、 D、8. 函数和 , 在同一直角坐标系中的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,以点为位似中心,把的各边放大为原来的2倍得到 , 下列说法错误的是( )
9. 如图,以点为位似中心,把的各边放大为原来的2倍得到 , 下列说法错误的是( ) A、 B、 C、 D、10. 如图,在中, , , 下列结论一定正确的是( )
A、 B、 C、 D、10. 如图,在中, , , 下列结论一定正确的是( )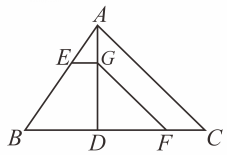 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,每小题3分,共24分)
-
11. 若四条线段a,b,c,d成比例,其中 , , , 则 .12. 若关于的一元二次方程有实根,则的取值范围是.13. 已知,菱形的周长为52,一条对角线长为10,则另一条对角线长为.14. 在某一时刻,将长为1.8米的竹竿竖直立在水平地面上,测得它的影长为3米,同时同地测得一栋楼的影长为35米,则这栋楼的高度为.15. 在一个不透明的袋子中,有若干个红球和白球,它们除颜色外完全相同,其中红球有12个,且从中摸出白球的概率为 , 则袋子中白球的个数为.16. 某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右。若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为.17. 如图,在矩形中, , .折叠该矩形,使点与点重合,点落在点处,折痕的长为.
 18. 如图,点是反比例函数的图象上一点,过点向轴作垂线,垂足为点 , 点、在轴上,且 , 则四边形的面积为.
18. 如图,点是反比例函数的图象上一点,过点向轴作垂线,垂足为点 , 点、在轴上,且 , 则四边形的面积为.
三、解答题(本大题共2小题,共22分.解答应写出必要的文字说明、证明过程或演算步骤)
-
19. 用适当的方法解下列一元二次方程.(1)、;(2)、.20. 已知, , , 是的三边,且 , , 求的面积.
四、解答题(本大题共2小题,共24分.解答应写出必要的文字说明、证明过程或演算步骤)
-
21. 四个完全相同的乒乓球,分别标注数字1、2、3、4,将它们放入一个不透明的盒子中.从盒子中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,记下数字后再放回.请用列表或画树状图的方法解决下列问题:(1)、求两次摸到的球上数字同时为偶数的概率;(2)、在上面的问题中,如果第一次摸出球后不放回,继续第二次摸球,求两次摸到的球上数字之和为偶数的概率.22. 如图,要使用长为27米的篱笆,一面利用墙(墙的最大可用长度为12米),围成中间隔有一道篱笆的长方形花圃.
 (1)、如果要围成面积为54平方米的花圃,那么的长为多少米?(2)、能否围成面积为90平方米的花圃?若能,请求出的长;若不能,请说明理由.
(1)、如果要围成面积为54平方米的花圃,那么的长为多少米?(2)、能否围成面积为90平方米的花圃?若能,请求出的长;若不能,请说明理由.五、解答题(本大题共1小题,共12分.解答应写出必要的文字说明、证明过程或演算步骤)
-
23. 如图,在中, , , 动点从点开始沿边向点匀速运动,运动速度为1cm/s,动点从点开始沿边向点匀速运动,运动速度为2cm/s,点和点同时出发.求两动点运动多长时间,以点、、为顶点的三角形与相似.

六、解答题(本大题共1小题,共12分.解答应写出必要的文字说明、证明过程或演算步骤)
-
24. 如图,小明同学为了测量路灯的高度,先将长2m的竹竿竖直立在水平地面上的处,测得竹竿的影长 , 然后将竹竿向远离路灯的方向移动5m到处,即 , 测得竹竿的影长(、为竹竿).求路灯的高度.

七、解答题(本大题共1小题,共12分.解答应写出必要的文字说明、证明过程或演算步骤)
-
25. 如图,平行四边形 , 对角线、相交于点 , , , 、是对角线上的两个动点,点从点开始向点匀速运动,点从点开始向点匀速运动,点和点同时出发,且运动速度均为 .
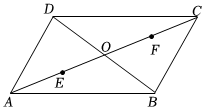 (1)、求证:当、运动过程中不与点重合时,四边形是平行四边形;(2)、若四边形为矩形,求动点、运动时间.
(1)、求证:当、运动过程中不与点重合时,四边形是平行四边形;(2)、若四边形为矩形,求动点、运动时间.八、解答题(本大题共1小题,共14分.解答应写出必要的文字说明、证明过程或演算步骤)
-
26. 如图,在中, , , .一次函数交轴于点 , 交反比例函数于、两点.
 (1)、求一次函数和反比例函数的解析式;(2)、求的面积;(3)、问:在直角坐标系中,是否存在一点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点的坐标;若不存在,请说明理由.
(1)、求一次函数和反比例函数的解析式;(2)、求的面积;(3)、问:在直角坐标系中,是否存在一点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点的坐标;若不存在,请说明理由.
-
-
-