浙江省金华市东阳市横店教共体八校联考2023-2024学年七年级下学期开学数学试题
试卷更新日期:2024-03-11 类型:开学考试
一、选择题(共10小题,满分30分,每小题3分)
-
1. 2024的相反数是A、 B、 C、2024 D、-20242. 2023年9月23日晚,以“潮起亚细亚”为主题”的杭州亚运会盛大开幕,本次亚运会观众预计达到570万人次,创下杭州历史之最。570万用科学记数法表示为( )A、 B、 C、 D、3. 在 , 3.14,0.5757757775……(相邻两个5之间7的个数逐次加1)中,无理数的个数为( )A、2 B、3 C、4 D、54. 下列运算正确的是A、 B、 C、 D、5. 下列说法正确的是A、单项式的系数为 B、多项式的次数为3 C、单项式的次数为7 D、是整式6. 有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
 A、 B、 C、 D、7. 如图,下列说法正确的是
A、 B、 C、 D、7. 如图,下列说法正确的是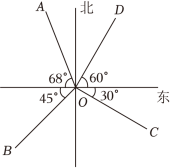 A、的方向是北偏西 B、的方向是西南方向 C、的方向是南偏东 D、的方向是北偏东8. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问多久后甲乙相逢?设乙出发x日,甲乙相逢,则可列方程( )A、 B、 C、 D、9. 将一张长方形纸片沿EF折叠,折叠后的位置 如图所示,若∠EFB=65°,则∠AED′等于( )
A、的方向是北偏西 B、的方向是西南方向 C、的方向是南偏东 D、的方向是北偏东8. 《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢?译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问多久后甲乙相逢?设乙出发x日,甲乙相逢,则可列方程( )A、 B、 C、 D、9. 将一张长方形纸片沿EF折叠,折叠后的位置 如图所示,若∠EFB=65°,则∠AED′等于( )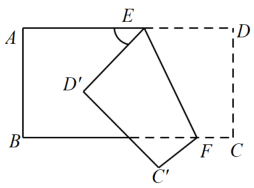 A、70° B、65° C、50° D、25°10. 如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形 , 两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积与(2)图长方形的面积的比是多少?
A、70° B、65° C、50° D、25°10. 如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形 , 两种方式未覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积与(2)图长方形的面积的比是多少?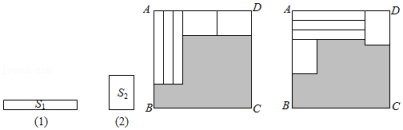 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共6小题,每小题4分,共24分)
-
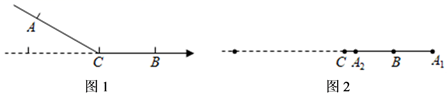
11. 若∠α=60°33',则∠α的补角为 .12. 方程是关于的一元一次方程,则 .13. 的平方根是14. 20.9506精确到十分位的近似值是 .15. 已知代数式的值为2,则代数式的值为 .16. 如图1,在一条可以折叠的数轴上有点A,B,C,其中点A,点B表示的数分别为﹣16和9,现以点C为折点,将数轴向右对折,点A对应的点A1落在B的右边;如图2,再以点B为折点,将数轴向左折叠,点A1对应的点A2落在B的左边.若A2、B之间的距离为3,则点C表示的数为.
三、解答题(共8小题,满分66分)
-
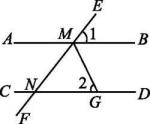
17. 计算:(1)、(2)、18. 解下列方程:(1)、(2)、19. 已知的平方根为 , 的算术平方根为4,求的立方根.20. 已知 , .(1)、化简:.(2)、当 , 时,求代数式的值.21. 如图,AB∥CD,EF分别交AB,CD于点M,N,∠1=52°,MG平分∠BMF交CD于点G,求∠2的度数.
 22. 某移动公司推出两款“套餐”,计费方式如下:
22. 某移动公司推出两款“套餐”,计费方式如下:套餐类别
套餐一
套餐二
通话不超时且
通话200分钟及以下,
通话250分钟及以下,
流量不超量
流量及以下,
流量及以下,
各种费用月费共计69元.
各种费用月费共计99元.
通话超时或
通话超时部分加收0.15元/分;
通话超时部分加收0.12元/分;
上网超量
流量超量部分加收2.5元 .
流量超量部分加收2元/ .
(1)、若某月小明通话时间为300分钟,上网流量为 , 则他按套餐一计费需要的费用是元;按套餐二计费需要的费用是元;(2)、若上网流量为 , 是否可能通话时间相同,按套餐一和套餐二的计费也相等?请你作出判断并说明理由.(3)、为迎接新春佳节到来,移动公司针对两款套餐推出限时优惠活动:套餐一对通话超时和上网超量部分的费用打8折;套餐二月费从99元降到90元。小明认为:“当通话超过250分钟,流量超过时,两款套餐费用差额为一确定的值.”你认为小明的判断正确吗?如果正确,请求出这一确定的值;如果不正确,请说明理由.23. 如图
【问题提出】已知∠BOC与∠AOC有共同的始边OC,且满足∠BOC=2∠AOC,若∠AOC=28°,求∠AOB的度数.
【问题解决】圆圆首先画出两个符合题意的图形,运用分类讨论的数学思想,解决问题.
在图①中,当射线OA在∠BOC的内部时,由题意易得∠AOB=28°;
在图②中,当射线OA在∠BOC的外部时,由题意易得∠AOB=84°.
【问题应用】请仿照这种方法,解决下面两个问题
(1)、如图③,已知点A,B,C在数轴上对应的数分别为﹣4,2,1,请在数轴上标出线段AC的中点D并写出D所表示的数;若数轴上存在点E,它到点C的距离恰好是线段AB的长,求线段DE的长.(2)、如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1﹣∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角).①若∠α=140°,求∠α的垂角;②如果一个角的垂角等于这个角的补角的 , 求这个角的度数.
24. 定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.如图①所示,若∠COD=∠AOB,则∠COD是∠AOB的内半角.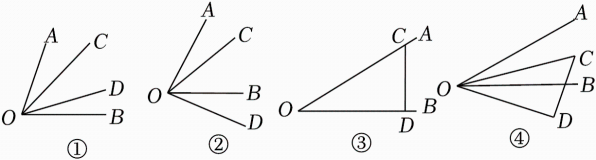 (1)、如图①所示,已知∠AOB=70°,∠AOC=15°,∠COD是∠AOB的内半角,则∠BOD= .(2)、如图②,已知∠AOB=63°,将∠AOB绕点O按顺时针方向旋转一个角度α(0<α<63°)至∠COD,当旋转的角度α为何值时,∠COB是∠AOD的内半角?(3)、已知∠AOB=30°,把一块含有30°角的三角板如图③叠放,将三角板绕顶点O以3°/秒的速度按顺时针方向旋转,如图④,问:在旋转一周的过程中,且射线OD始终在∠AOB的外部,射线OA,OB,OC,OD能否构成内半角?若能,请直接写出旋转的时间;若不能,请说明理由.
(1)、如图①所示,已知∠AOB=70°,∠AOC=15°,∠COD是∠AOB的内半角,则∠BOD= .(2)、如图②,已知∠AOB=63°,将∠AOB绕点O按顺时针方向旋转一个角度α(0<α<63°)至∠COD,当旋转的角度α为何值时,∠COB是∠AOD的内半角?(3)、已知∠AOB=30°,把一块含有30°角的三角板如图③叠放,将三角板绕顶点O以3°/秒的速度按顺时针方向旋转,如图④,问:在旋转一周的过程中,且射线OD始终在∠AOB的外部,射线OA,OB,OC,OD能否构成内半角?若能,请直接写出旋转的时间;若不能,请说明理由.