浙江省宁波市余姚市2023-2024学年八年级上学期期末数学试卷
试卷更新日期：2024-03-11 类型：期末考试
一、选择题。（每小题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求）
-
1. 围棋是中华民族发明的迄今最久远、最复杂的智力博弈活动之一，下列围棋图案中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 在平面直角坐标系中，点（4，﹣3）在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 直线y＝﹣x+3与x轴的交点坐标是（ ）A、（0，3） B、（0，﹣3） C、（3，0） D、（﹣3，0）4. 已知a＜b ， 则下列不等式中错误的是（ ）A、a﹣2＜b﹣2 B、 C、﹣2a＜﹣2b D、a+2＜b+25. 下列各组长度的线段，不能组成直角三角形的是（ ）A、5，12，13 B、 C、2，3，4 D、6，8，106. 下列命题中是真命题的是（ ）A、等边三角形一条边上的高线也是该条边上的中线 B、有一个角是60°的三角形是等边三角形 C、等腰三角形一定是锐角三角形 D、有一个角对应相等的两个等腰三角形全等7. 如图，AB=AC，点D，E分别在AB，AC上，补充下列一个条件后，不能判断△ABE ≌△ACD的是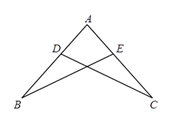
A、∠B=∠C B、AD=AE C、∠BDC=∠CEB D、BE=CD8. 如图，在Rt△ABC中，AC＝BC ， 点D为AB中点．∠GDH＝90°，∠GDH绕点D旋转，DG ， DH分别与边AC ， BC交于E ， F两点．下列结论中错误的是（ ）
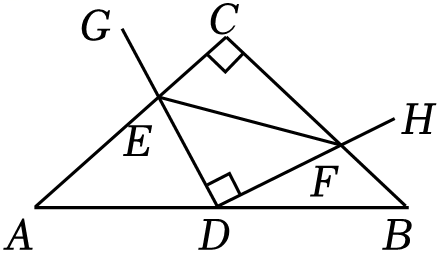A、CE＝BF B、AE+CF＝AB C、AE2+BF2＝EF2 D、△DEF始终为等腰直角三角形9. 我们规定：当k ， b为常数，k≠0，b≠0，k≠b时，一次函数y＝kx+b与y＝bx+k互为交换函数，例如：y＝2x+3的交换函数为y＝3x+2．一次函数y＝kx+5与它的交换函数图象的交点横坐标为（ ）A、1 B、﹣1 C、5 D、﹣510. 如图，在△ABC中，AB＝AC＝16，BC＝12，AF⊥BC于点F ， BE⊥AC于点E ， D为AB的中点，M为EF的中点，则DM的长为（ ）
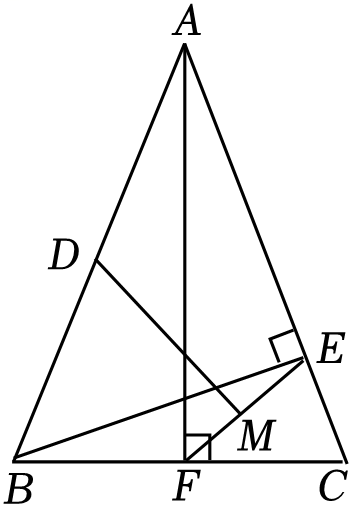A、7 B、8 C、 D、二、填空题。（每小题4分，共24分）
-
11. 将“a是正数”用不等式表示为 ．12. 写出一个经过点（1，2）的函数表达式 ．13. 说明“互补的两个角一定是一个锐角一个钝角”是假命题，可举出的反例是 ．14. 一次函数y=（2m﹣6）x+5中，y随x的增大而减小，则m的取值范围是 ．15. 如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿着直线AD折叠，使它落在斜边AB上，且与AE重合，则CD的长为 cm．
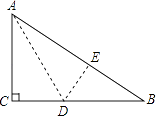16. 如图，边长为5的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成，连结AF并延长交BC于点M ． 若AH＝HE ， 则CM的长为 ．
三、解答题。（第17、18题各6分，第19、20、21题各8分，第22、23题各9分，第24题12分，共66分）
-
17. 解一元一次不等式组： ．18. 在平面直角坐标系中，已知△ABC的位置如图所示．
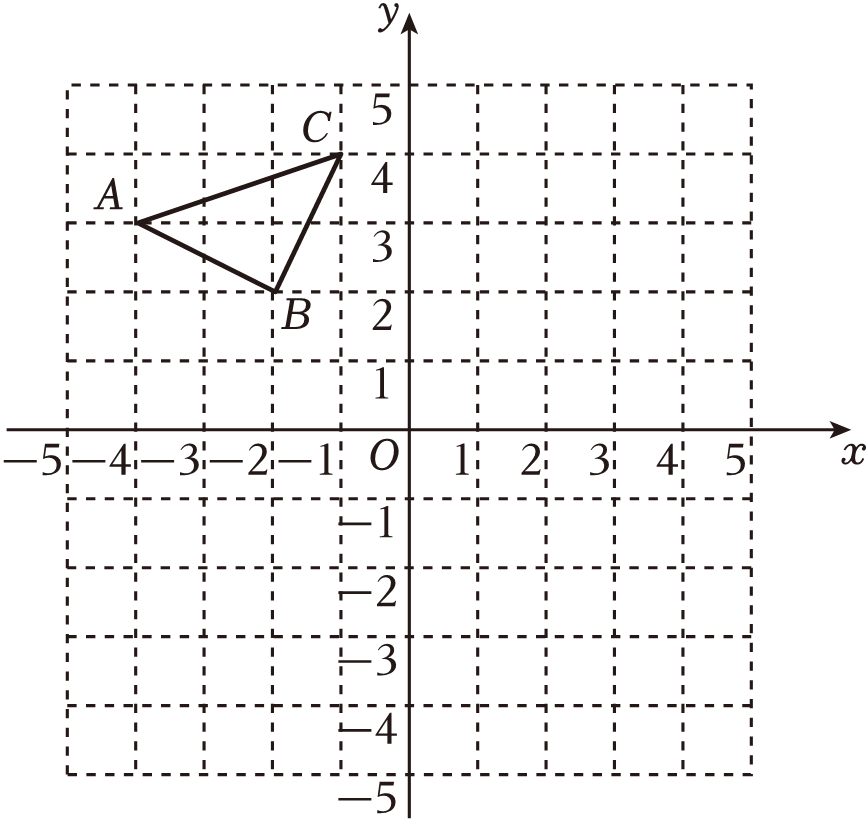(1)、请作出△ABC向右平移5个单位后得到的△A1B1C1（其中点A1 ， B1 ， C1分别是点A ， B ， C的对应点，不写画法）；(2)、写出点B关于x轴的对称点B2的坐标．19. 如图，在△ABC与△DCB中，AC与BD交于点E ， 且∠A＝∠D ， AB＝DC ．
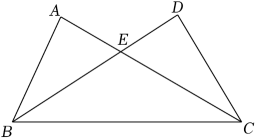(1)、求证：△ABE≌△DCE；(2)、求证：∠EBC＝∠ECB ．20. 小聪用100元钱去购买笔记本和钢笔．已知每本笔记本2元，每支钢笔5元．(1)、若小聪已经购买了15支钢笔，问最多还能买几本笔记本？(2)、若小聪想购买笔记本和钢笔共30件，问最多能买几支钢笔？21. 如图，在△ABC中，AB＝AC＝5，BC＝6，点D在AC边上，BD＝AB ．
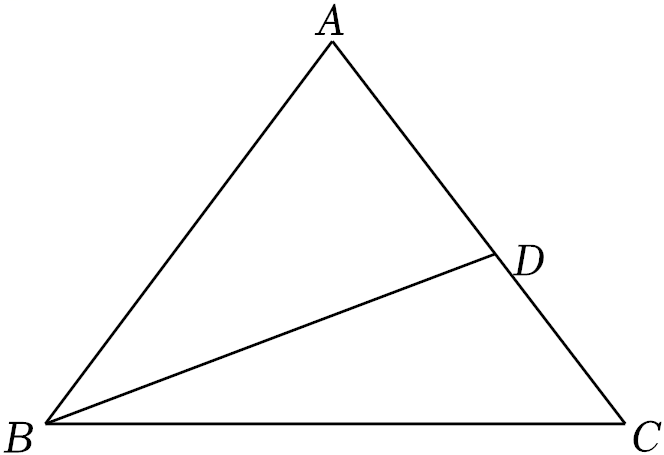(1)、求△ABC的面积；(2)、求AD的长．22. 已知甲、乙两城市之间每隔2h有一列动车组列车以相同的速度从甲城开往乙城．如图，OA是第一列动车组列车离开甲城的路程s（km）与运行时间t（h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运行时间t（h）的函数图象．请根据图中的信息，解答下列问题：
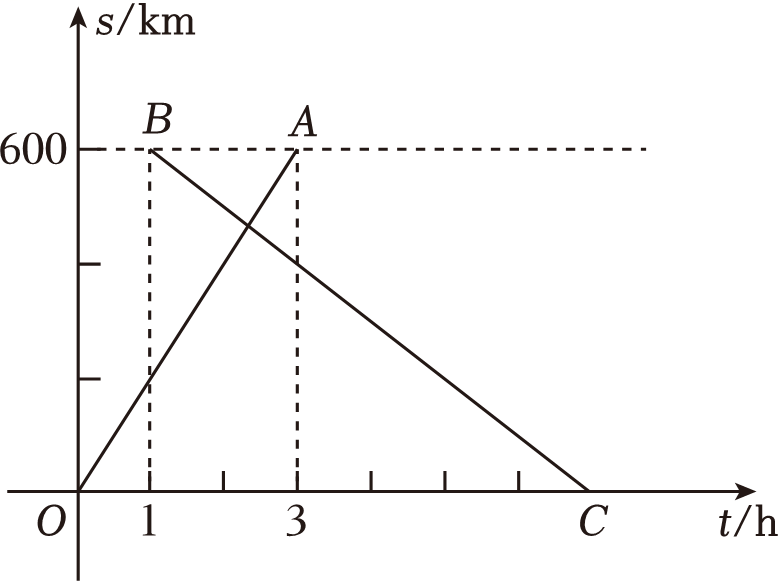(1)、从图象可知，动车组列车的行驶速度为 km/h；(2)、请直接在图中画出第二列动车组列车离开甲城的路程s与时间t的函数图象；(3)、若普通快车的速度为100km/h ， 问第一列动车组列车出发多长时间后与这列普通快车相遇？23. 如图，∠BCD＝90°，BC＝CD ， CD⊥AD ， AC、BD交于点E ， DA＝DE ， BN平分∠DBC ， 交AC于点M ， 交DC于点N ．
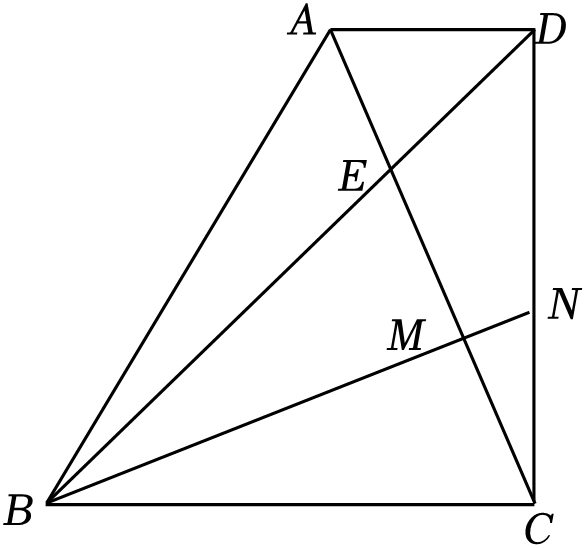(1)、求∠ACD的度数；(2)、求证：DB＝DA+DC；(3)、求证：AE＝2MN ．24. 如图，在平面直角坐标系中，点A（0，8），B（﹣4，0），C（4，0），给出如下定义：若P为△ABC内（不含边界）一点，且BP与△APC的一条边相等，则称点P为△ABC的和谐点．
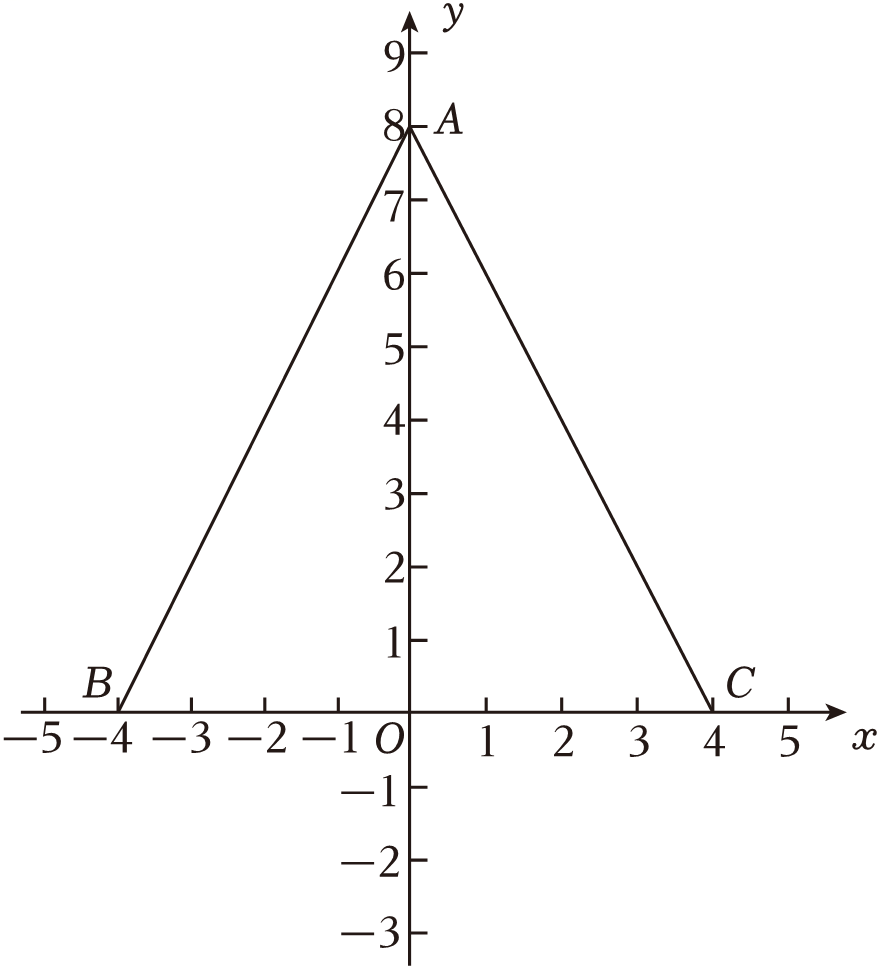(1)、在P1（﹣1，1），P2（2，2），P3（0，5）中，△ABC的和谐点是 ；(2)、若点P为△ABC的和谐点，且∠ABP＝45°，求点P的坐标；(3)、直线l为过点M（0，m）且与x轴平行的直线，若直线l上存在△ABC的二个和谐点，请直接写出m的取值范围．