广东省深圳市2023-2024学年九年级数学上学期社团冬季素养展示活动

试卷更新日期：2024-03-11 类型：期末考试

进入出卷网下载

一、选择题（每小题5分，共40分）

1. 如图，点 $P_{1} ~ P_{8}$ 是 $⊙ O$ 的八等分点.若 $△ P_{1} P_{3} P_{7}$ ，四边形 $P_{3} P_{4} P_{6} P_{7}$ 的周长分别为a，b，下列正确的是（）

A、 $a < b$ B、 $a = b$ C、 $a > b$ D、a，b大小无法比较

查看试题解析
2. 皮克定理是格点几何学中的一个重要定理，它揭示了以格点为顶点的多边形的面积 $S = N + \frac{1}{2} L - 1$ ，其中 $N ， L$ 分别表示这个多边形内部与边界上的格点个数．在平面直角坐标系中，横、纵坐标都是整数的点为格点．已知 $A (0 ， 30)$ ， $B (20 ， 10) ， O (0 ， 0)$ ，则 $△ A B O$ 内部的格点个数是（）

A、266 B、270 C、271 D、285

查看试题解析
3. 第二十四届国际数学家大会会微的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图，在由四个全等的直角三角形 $(△ D A E ， △ A B F ， △ B C G ， △ C D H)$ 和中间一个小正方形EFGH拼成的大正方形ABCD中， $∠ A B F > ∠ B A F$ ，连接BE.设 $∠ B A F = α ， ∠ B E F = β$ ，若正方形EFGH与正方形ABCD的面积之比为 $1 ： n ， t a n α = t a n^{2} β$ ，则 $n =$ （）

A、5 B、4 C、3 D、2

查看试题解析
4. 直三棱柱的表面展开图如图所示， $A C = 3$ ， $B C = 4$ ， $A B = 5$ ，四边形 $A M N B$ 是正方形，将其折叠成直三棱柱后，下列各点中，与点 $C$ 距离最大的是（）

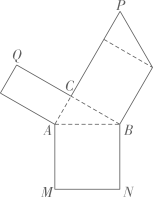A、点 $M$ B、点 $N$ C、点 $P$ D、点 $Q$

查看试题解析
5. 若k为任意整数，则 $(2 k + 3)^{2} - 4 k^{2}$ 的值总能（）

A、被2整除 B、被3整除 C、被5整除 D、被7整除

查看试题解析
6. 我们发现： $\sqrt{6 + 3} = 3 ， \sqrt{6 + \sqrt{6 + 3}} = 3 ， \sqrt{6 + \sqrt{6 + \sqrt{6 + 3}}} = 3$ ， …… $\underset{n 个根号}{\underset{︸}{\sqrt{6 + \sqrt{6 + \sqrt{6 + \dots + \sqrt{6 + \sqrt{6 + 3}}}}}}} = 3$ ，一般地，对于正整数a，b，如果满足 $\underset{n 个根号}{\underset{︸}{\sqrt{b + \sqrt{b + \sqrt{b + \dots + \sqrt{b + \sqrt{b + a}}}}}}} = a$ 时，称 $(a ， b)$ 为一组完美方根数对.如上面（3，6）是一组完美方根数对，则下面4个结论：①（4，12）是完美方根数对；②（9.91）是完美方根数对；若（a，380）是完美方根数对，则a=20；④若（x，y）是完美方根数对，则点P（x，y）在抛物线y=x²-x上，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，PA切⊙O于点A，点B在⊙O内，BP交⊙O于点C，若PA=6，PC=4，CB=2，OB=1，则⊙O的半径为（）

A、2 B、3 C、 $\sqrt{6}$ D、 $\sqrt{7}$

查看试题解析
8. $2 \times 3$ 的矩形被分为6个 $1 \times 1$ 的区域，现在：有6种颜色供选择，要求每个区域染一种颜色，并且相邻区域颜色不同，则一共有（）种染色方案？

A、13230 B、27000 C、12300 D、14400

查看试题解析

二、填空题（每题5分，共20分）

9. 如图，四边形ABCD内接于 $⊙ O$ ，它的3个外甪 $∠ E A B ， ∠ F B C ， ∠ G C D$ 的度数之比为1：2：4，则 $∠ D =$ $^{°}$ .

查看试题解析
10. 矩形ABCD中， $M$ 为对角线BD的中点，点 $N$ 社边AD上，且 $A N = A B = 1$ .当以点D，M，N为顶点的三角形是直角三角形时，AD的长为.

查看试题解析
11. 设 $f (x)$ 是整系数多项式，使得 $f (19) = f (94) = 1994$ ，且常数项的绝对值小于1000，则常数项为.

查看试题解析
12. 已知： $\frac{(a - b) (b - c) (c - a)}{(a + b) (b + c) (c + a)} = \frac{5}{132}$ ，则 $\frac{a}{a + b} + \frac{b}{b + c} + \frac{c}{c + a} =$ .

查看试题解析

三、解答题（共4小题，共40分）

13. 为提升学生身体素质，落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神．某校利用课后服务时间，在八年级开展“体育赋能，助力成长”班级篮球赛，共 $16$ 个班级参加．

(1)、比赛积分规定：每场比赛都要分出胜负，胜一场积 $3$ 分，负一场积 $1$ 分．某班级在 $15$ 场比赛中获得总积分为 $41$ 分，问该班级胜负场数分别是多少？

(2)、投篮得分规则：在 $3$ 分线外投篮，投中一球可得 $3$ 分，在 $3$ 分线内 $($ 含 $3$ 分线 $)$ 投篮，投中一球可得 $2$ 分，某班级在其中一场比赛中，共投中 $26$ 个球 $($ 只有 $2$ 分球和 $3$ 分球 $)$ ，所得总分不少于 $56$ 分，问该班级这场比赛中至少投中了多少个 $3$ 分球？

查看试题解析
14. 第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行，我国冬奥选手取得了9块金、4块银牌、2块铜牌，为祖国赢得了荣誉，激起了国人对冰雪运动的热情．某地模仿北京首钢大跳台建一个滑雪大跳台（如图1），它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成．图2是其示意图，知助滑坡道AF=50米，弧形跳台的跨度FG=7米，顶端E到BD的距离为40米，HG∥BC，
$△ F H = 4 0^{°} ， ∠ E F G = 2 5^{°} ， ∠ E C B = 3 6^{°}$ .求此大跳台最高点 $A$ 距地面BD的距离是多少米？（结果保留小数）（参考数据： $s i n 4 0^{°} \approx 0.64 ， c o s 4 0^{°} \approx 0.77 ， t a n 4 0^{°} \approx 0.84 ， s i n 2 5^{°} \approx 0.42 ， c o s 2 5^{°} \approx 0.91 ， t a n 2 5^{°} \approx 0.47$ ， $13 6^{°} \approx 0.59 ， c o s 3 6^{°} \approx 0.81 ， t a n 3 6^{°} \approx 0.73)$

查看试题解析
15. 已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G.

(1)、如左图，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得 $\frac{D E}{C F} = \frac{A D}{C D}$ 成立？并证明你的结论；

(2)、如右图，若 $B A = B C = 6 ， D A = D C = 8 ， ∠ B A D = 9 0^{°} ， D E ⊥ C F$ ，则 $\frac{D E}{C F} =$ 。

查看试题解析
16. 【定义】在平面内，把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值，称为这两个图形之间的距离，即A，B分别是图形 $M$ 和图形 $N$ 上任意一点，当AB的长最小时，称这个最小值为图形 $M$ 与图形 $N$ 之间的距离.
例如，如图1， $A B ⊥ l_{1}$ ，线段AB的长度称为点， $A$ 与直线 $l_{1}$ 之间的距离，当 $l_{2} / l_{1}$ 时，线段AB的长度也是 $l_{1}$ 与 $l_{2}$ 之间的距离.
【应用】

(1)、如图2，在等腰Rt $△ B A C$ 中， $∠ A = 9 0^{°} ， A B = A C$ ，点 $D$ 为AB边上一点，过点 $D$ 作 $D E ‖ B C$ 交AC于点 $E$ .若 $A B = 6 ， A D = 4$ ，则DE与BC之间的距离是

(2)、如图3，已知直线 $l_{3} ： y = - x + 4$ 与双曲线 $C ： y = \frac{k}{x} (x > 0)$ 交于 $A (1 ， m)$ 与 $B$ 两点，点 $A$ 与点， $B$ 之间的距离是，点 $O$ 与双曲线 $C_{1}$ 之间的距离是；

(3)、【拓展】按规定，住宅小区的外延到高速路的距离不超过80m时，需要在高速路旁修建与高速路相同走向的隔音屏障（如图4）.有一条“东南-西北”走向的笔直高速路，路旁某住宅小区建筑外延呈双曲线的形状，它们之间的距离小于80m.现以高速路上某一合适位置为坐标原点，建立如图5所示的直角坐标系，此时高速路所在直线l4的函数表达式为 $y = - x$ ，小区外延所在双曲线 $C_{2}$ 的函数表达式为 $y = \frac{2400}{x} (x$ $> 0)$ ，那么需要在高速路旁修建隔音屏障的长度是多少？

查看试题解析