广东省湛江经济技术开发区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-11 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 下列四种网络运营商的徽标中，符合轴对称图形特征的为（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x + 3}{x - 2}$ 的值为 $0$ ，则 $x$ 的值为（）

A、 $x = - 3$ B、 $x = 2$ C、 $x \neq - 3$ D、 $x \neq 2$

查看试题解析
3. 下列图形中有稳定性的是（）

A、三角形 B、平行四边形 C、长方形 D、正八方形

查看试题解析
4. 要使分式 $\frac{3}{x - 1}$ 有意义，则x的取值范围是（）

A、x≠1 B、x＞1 C、x＜1 D、x≠﹣1

查看试题解析
5. 下列长度的三根木条首尾相连，能组成三角形的是（　　）

A、3，4，8 B、8，7，15 C、2，2，3 D、5，5，11

查看试题解析
6. 下列运算中正确的是（）

A、 $a \cdot a^{2} = a^{2}$ B、 ${(a^{3})}^{2} = a^{6}$ C、 $x^{6} \div x^{3} = x^{2}$ D、 ${(3 a)}^{3} = 9 a^{3}$

查看试题解析
7. 在平面直角坐标系中，点 $(2 ， - 1)$ 关于x轴对称的点是（）

A、 $(2 ， 1)$ B、 $(1， - 2)$ C、 $(- 1 ， 2)$ D、 $(- 2 ， - 1)$

查看试题解析
8. 如图，在△ABC中，∠A=70°，直线DE分别与AB，AC交于D，E两点，则∠1+∠2=（）

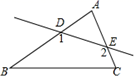A、110° B、140° C、180° D、250°

查看试题解析
9. 如图， $A C$ ， $B D$ 相交于点 $O$ ， $O A = O C$ ，要使 $△ A O B ≌ △ C O D$ ，则补充下列其中一个条件后，不一定能推出 $△ A O B ≌ △ C O D$ 的是（）

A、 $∠ A = ∠ C$ B、 $∠ B = ∠ D$ C、 $A B = C D$ D、 $O B = O D$

查看试题解析
10. 如图，在 $△ A B C$ 中，已知点D，E，F分别为边 $B C$ ， $A D$ ， $C E$ 的中点，且 $S_{△ A B C} = 12 {cm}^{2}$ ，则阴影部分的面积等于（）

A、 $1 {cm}^{2}$ B、 ${2cm}^{2}$ C、 $3 {cm}^{2}$ D、 ${4cm}^{2}$

查看试题解析

二、填空题（本大题共小题，每小题6分，共18分）

11. 因式分解 $5 a^{2} - a =$ ．

查看试题解析
12. 等腰三角形有一个角是 $10 0^{∘}$ ，则这个等腰三角形的一个底角为．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ C A B$ 的外角等于 $120 °$ ， $∠ B$ 等于 $40 °$ ，则 $∠ C$ 的度数是．

查看试题解析
14. 有一种病毒的直径为0.000068米，用科学记数法可表示为米．

查看试题解析
15. 一个多边形的内角和是 $720 °$ ，则这个多边形的边数为．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B C = 4$ ， $△ A B C$ 的面积为 $20$ ， $A B$ 的垂直平分线 $E F$ 分别交 $A C$ ， $A B$ 边于点 $E$ ， $F$ ，若 $D$ 为 $B C$ 边的中点， $M$ 为线段 $E F$ 上一动点，则 $B M + D M$ 的最小值为．

查看试题解析

三、解答题（本大题共9小题，满分72分，解答应写出文字说明、证明过程或演算步骤．）

17. 计算： ${(- 1)}^{3} + {(π + 2022)}^{0} + {(\frac{1}{2})}^{- 2}$

查看试题解析
18. $(m + 2 n) (3 n - m)$

查看试题解析
19. 先化简，再求值： $(\frac{x}{x - 2} - \frac{1}{x - 2}) \div \frac{x^{2} - x}{x^{2} - 4}$ ，其中 $x = 3$ ．

查看试题解析
20. 如图，BD∥AC ， BD＝BC ，且BE＝AC ．求证：∠D＝∠ABC ．

查看试题解析
21. 已知：如图，在△ABC中，∠B=30°，∠C=90°．

(1)、作AB的垂直平分线DE，交AB于点E，交BC于点D；（要求：尺规作图，保留作图痕迹，不写作法和证明）

(2)、连接DA，若BD=6，求CD的长．

查看试题解析
22. 习近平总书记在主持召开中央农村工作会议中指出：“坚持中国人的饭碗任何时候都要牢牢端在自己手中，饭碗主要装中国粮．”某粮食生产基地为了落实习近平总书记的重要讲话精神，积极扩大粮食生产规模，计划投入一笔资金购买甲、乙两种农机具，已知 $1$ 件甲种农机具比 $1$ 件乙种农机具多 $1$ 万元，用 $15$ 万元购买甲种农机具的数量和用 $10$ 万元购买乙种农机具的数量相同．

(1)、求购买 $1$ 件甲种农机具和 $1$ 件乙种农机具各需多少万元？

(2)、若该粮食生产基地计划购买甲、乙两种农机具共 $20$ 件，且购买的总费用不超过 $46$ 万元，则甲种农机具最多能购买多少件？

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ B = 60 °$ ，点 $M$ 从点 $B$ 出发沿射线 $B C$ 方向，在射线 $B C$ 上运动．在点 $M$ 运动的过程中，连结 $A M$ ，并以 $A M$ 为边在射线 $B C$ 上方，作等边 $△ A M N$ ，连结 $C N$ ．

(1)、当 $∠ B A M =$ $°$ 时， $A B = 2 B M$ ；

(2)、请添加一个条件：，使得 $△ A B C$ 为等边三角形；

(3)、在（2）的条件下，当 $△ A B C$ 为等边三角形时，求证： $C N + C M = A C$ ；

查看试题解析
24. 【探究】如图①，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成图②的长方形．

(1)、请你分别表示出这两个图形中阴影部分的面积：图①图②；

(2)、比较两图的阴影部分面积，可以得到乘法公式：(用字母a、b表示)；

(3)、【应用】请应用这个公式完成下列各题：
①已知2m﹣n=3，2m+n=4，则4m²﹣n²的值为 ▲ ；
②计算：(x﹣3)(x+3)(x²+9)．

(4)、【拓展】计算 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) ⋯ (2^{32} + 1)$ 的结果为．

查看试题解析
25. 如图，在平面直角坐标系中 $A (a ， 0) ， B (0 ， b)$ ，满足 $a^{2} - 4 a + 4 + | b - 4 | = 0$

(1)、求 $A ， B$ 两点的坐标；

(2)、 $∠ O B A$ 的平分线 $B C$ 与 $∠ O A B$ 的外角平分线AM交于点C，求 $∠ C$ 的度数；

(3)、在平面内是否存在点P，使 $Δ A B P$ 为等腰直角三角形？若存在，请写出点P的个数，并直接写出其中两个点的坐标；若不存在，请说明理由.

查看试题解析