2023年湖北省中考数学真题分类汇编:04 图形与几何
试卷更新日期:2024-03-11 类型:二轮复习
一、选择题
-
1. 如图,已知点C为圆锥母线的中点,为底面圆的直径, , , 一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为( )
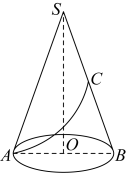 A、5 B、 C、 D、2. 如图,将四根木条用钉子钉成一个矩形框架 , 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( )
A、5 B、 C、 D、2. 如图,将四根木条用钉子钉成一个矩形框架 , 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( ) A、四边形由矩形变为平行四边形 B、对角线的长度减小 C、四边形的面积不变 D、四边形的周长不变3. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )
A、四边形由矩形变为平行四边形 B、对角线的长度减小 C、四边形的面积不变 D、四边形的周长不变3. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )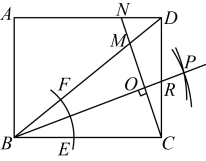 A、 B、 C、 D、44. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ).
A、 B、 C、 D、44. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ). A、 B、 C、 D、5. 下列图案中, 是中心对称图形.( )A、
A、 B、 C、 D、5. 下列图案中, 是中心对称图形.( )A、 B、
B、 C、
C、 D、
D、 6. 如图,有一张矩形纸片先对折矩形 , 使与重合,得到折痕 , 把纸片展平再一次折叠纸片,使点落在上,并使折痕经过点 , 得到折痕 , 同时得到线段 , 观察所得的线段,若 , 则( )
6. 如图,有一张矩形纸片先对折矩形 , 使与重合,得到折痕 , 把纸片展平再一次折叠纸片,使点落在上,并使折痕经过点 , 得到折痕 , 同时得到线段 , 观察所得的线段,若 , 则( ) A、 B、 C、 D、7. 如图,根据三视图,它是由个正方体组合而成的几何体.( )
A、 B、 C、 D、7. 如图,根据三视图,它是由个正方体组合而成的几何体.( )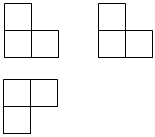 A、 B、 C、 D、8. 如图,在中,按以下步骤作图:分别以点 , 为圆心,大于的长为半径画弧,两弧相交于 , 两点,和交于点;以点为圆心,长为半径画弧,交于点;分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点 , 连接 , 和交于点 , 连接若 , , 则的长为( )
A、 B、 C、 D、8. 如图,在中,按以下步骤作图:分别以点 , 为圆心,大于的长为半径画弧,两弧相交于 , 两点,和交于点;以点为圆心,长为半径画弧,交于点;分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点 , 连接 , 和交于点 , 连接若 , , 则的长为( ) A、 B、 C、 D、9. 将含角的直角三角板按如图方式摆放,已知 , , 则( )
A、 B、 C、 D、9. 将含角的直角三角板按如图方式摆放,已知 , , 则( )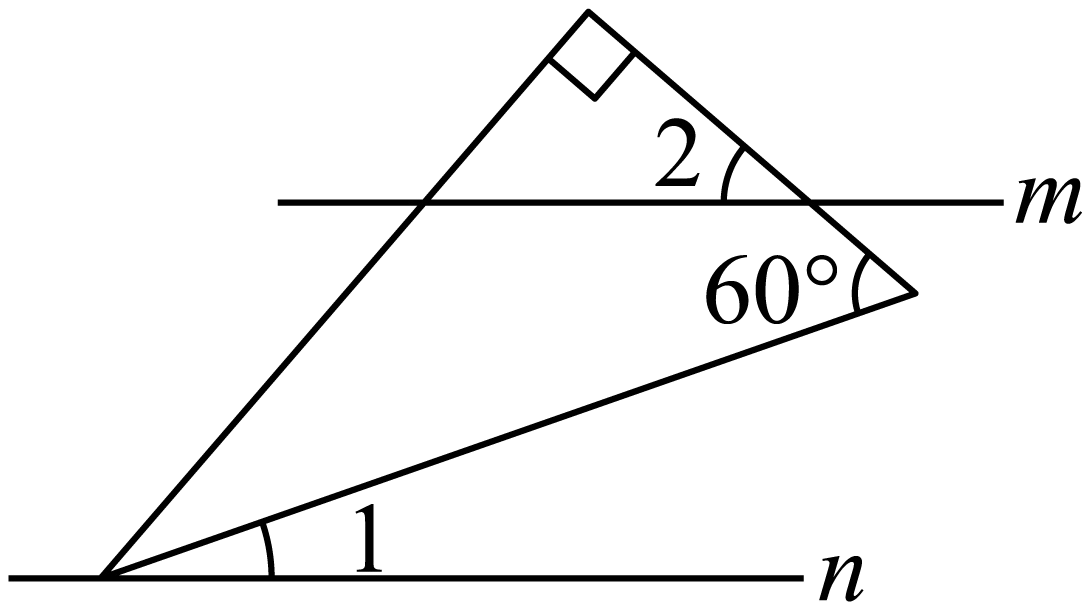 A、 B、 C、 D、10. 如图,在中,分别交于点D , E , 交于点F , , , 则的长为( )
A、 B、 C、 D、10. 如图,在中,分别交于点D , E , 交于点F , , , 则的长为( )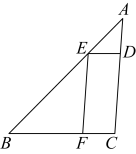 A、 B、 C、2 D、311. 如图,在中,直径与弦相交于点P,连接 , 若 , , 则( )
A、 B、 C、2 D、311. 如图,在中,直径与弦相交于点P,连接 , 若 , , 则( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )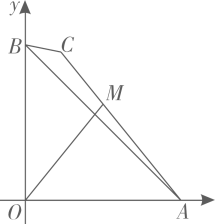 A、( , ) B、( , ) C、( , ) D、( , )13. 如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点外接圆的一部分,小正方形边长为1,图中阴影部分的面积为( )
A、( , ) B、( , ) C、( , ) D、( , )13. 如图,在的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中的圆弧为格点外接圆的一部分,小正方形边长为1,图中阴影部分的面积为( ) A、 B、 C、 D、14. 如图,直线分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转得到△CAD,则点B的对应点D的坐标是( )
A、 B、 C、 D、14. 如图,直线分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转得到△CAD,则点B的对应点D的坐标是( ) A、(2,5) B、(3,5) C、(5,2) D、( , 2)15. 如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,B为上一点,OB⊥AC于D. 若AC=m,BD=150m,则的长为( )
A、(2,5) B、(3,5) C、(5,2) D、( , 2)15. 如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,B为上一点,OB⊥AC于D. 若AC=m,BD=150m,则的长为( ) A、m B、m C、m D、m16. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( )
A、m B、m C、m D、m16. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( ) A、米 B、米 C、米 D、米17. 如图,在四边形中, , 以为圆心,为半径的弧恰好与相切,切点为 . 若 , 则的值是( )
A、米 B、米 C、米 D、米17. 如图,在四边形中, , 以为圆心,为半径的弧恰好与相切,切点为 . 若 , 则的值是( )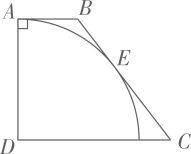 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
18. 若正n边形的一个外角为 , 则 .19. 如图,将▱绕点逆时针旋转到▱的位置,使点落在上,与交于点若 , , , 则从“ , , ”中选择一个符合要求的填空; .
 20. 《九章算术》被称为人类科学史上应用数学的“算经之首”.书中记载:“今有户不知高、广,竿不知长短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?”译文:今有门,不知其高宽;有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽和对角线的长各是多少(如图)?答:门高、宽和对角线的长分别是尺.
20. 《九章算术》被称为人类科学史上应用数学的“算经之首”.书中记载:“今有户不知高、广,竿不知长短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?”译文:今有门,不知其高宽;有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽和对角线的长各是多少(如图)?答:门高、宽和对角线的长分别是尺. 21.
21.如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为
 22. 如图,已知点 , 点B在y轴正半轴上,将线段绕点A顺时针旋转到线段 , 若点C的坐标为 , 则 .
22. 如图,已知点 , 点B在y轴正半轴上,将线段绕点A顺时针旋转到线段 , 若点C的坐标为 , 则 . 23. 如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且 . 若A(9,3),则A1点的坐标是 .
23. 如图,在平面直角坐标系中,△ABC与△A1B1C1位似,原点O是位似中心,且 . 若A(9,3),则A1点的坐标是 . 24. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)
24. 如图,无人机在空中A处测得某校旗杆顶部B的仰角为30o , 底部C的俯角为60o , 无人机与旗杆的水平距离AD为6m,则该校的旗杆高约为m.( , 结果精确到0.1)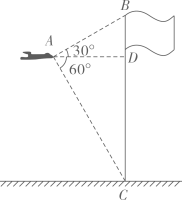 25. 如图,在中, , 则的度数为 .
25. 如图,在中, , 则的度数为 .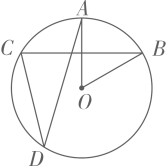 26. 如图,在矩形中, , M是边上一动点(不含端点),将沿直线对折,得到 . 当射线交线段于点P时,连接 , 则的面积为;的最大值为 .
26. 如图,在矩形中, , M是边上一动点(不含端点),将沿直线对折,得到 . 当射线交线段于点P时,连接 , 则的面积为;的最大值为 .
三、作图题
-
27. 已知正六边形 , 请仅用无刻度的直尺完成下列作图(保留作图痕迹,不写作法,用虚线表示作图过程,实线表示作图结果).
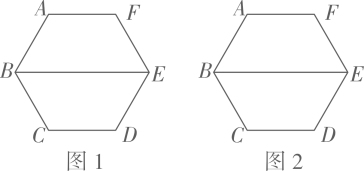 (1)、在图1中作出以为对角线的一个菱形;(2)、在图2中作出以为边的一个菱形 .28. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,正方形四个顶点都是格点,是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、在图1中作出以为对角线的一个菱形;(2)、在图2中作出以为边的一个菱形 .28. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,正方形四个顶点都是格点,是上的格点,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.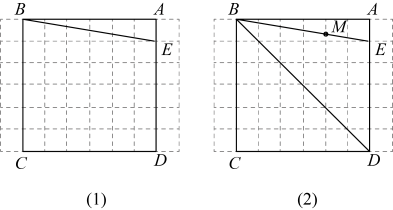 (1)、在图(1)中,先将线段绕点顺时针旋转 , 画对应线段 , 再在上画点 , 并连接 , 使;(2)、在图(2)中,是与网格线的交点,先画点关于的对称点 , 再在上画点 , 并连接 , 使 .
(1)、在图(1)中,先将线段绕点顺时针旋转 , 画对应线段 , 再在上画点 , 并连接 , 使;(2)、在图(2)中,是与网格线的交点,先画点关于的对称点 , 再在上画点 , 并连接 , 使 .四、解答题
-
29. 如图,在平面直角坐标系中,抛物线与轴交于两点 , , 与轴交于点 .
 (1)、求此抛物线的解析式;(2)、已知抛物线上有一点 , 其中 , 若 , 求的值;(3)、若点 , 分别是线段 , 上的动点,且 , 求的最小值.30. 如图,为的直径,和相交于点 , 平分 , 点在上,且 , 交于点 .
(1)、求此抛物线的解析式;(2)、已知抛物线上有一点 , 其中 , 若 , 求的值;(3)、若点 , 分别是线段 , 上的动点,且 , 求的最小值.30. 如图,为的直径,和相交于点 , 平分 , 点在上,且 , 交于点 . (1)、求证:是的切线;(2)、求证:;(3)、已知 , 求的值.31. 小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点 , 处测出点的仰角度数,可以求出信号塔的高.如图,的长为 , 高为 . 他在点处测得点的仰角为 , 在点处测得点的仰角为 , 在同一平面内.你认为小王同学能求出信号塔的高吗?若能,请求出信号塔的高;若不能,请说明理由.(参考数据: , , , 结果保留整数)
(1)、求证:是的切线;(2)、求证:;(3)、已知 , 求的值.31. 小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点 , 处测出点的仰角度数,可以求出信号塔的高.如图,的长为 , 高为 . 他在点处测得点的仰角为 , 在点处测得点的仰角为 , 在同一平面内.你认为小王同学能求出信号塔的高吗?若能,请求出信号塔的高;若不能,请说明理由.(参考数据: , , , 结果保留整数) 32. 如图,在矩形中,点是的中点,将矩形沿所在的直线折叠,的对应点分别为 , , 连接交于点 .
32. 如图,在矩形中,点是的中点,将矩形沿所在的直线折叠,的对应点分别为 , , 连接交于点 . (1)、若 , 求的度数;(2)、连接EF , 试判断四边形的形状,并说明理由.33. 为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形 , 斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米, , 求斜坡的长.(结果精确到米)(参考数据:)
(1)、若 , 求的度数;(2)、连接EF , 试判断四边形的形状,并说明理由.33. 为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形 , 斜面坡度是指坡面的铅直高度与水平宽度的比.已知斜坡长度为20米, , 求斜坡的长.(结果精确到米)(参考数据:)
五、实践探究题
-
34. 【问题呈现】
和都是直角三角形, , 连接 , , 探究 , 的位置关系.
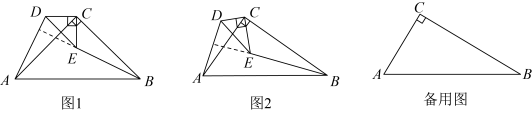 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
35. 某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)型抛物线图象.发现:如图1所示,该类型图象上任意一点P到定点F(0,)的距离PF,始终等于它到定直线l:y=的距离PN (该结论不需要证明).他们称:定点F为图象的焦点,定直线l为图象的准线,y=叫做抛物线的准线方程.准线l与y轴的交点为H.其中原点O为FH的中点,FH=2OF= . 例如,抛物线y=2x2 , 其焦点坐标为F(0,),准线方程为l:y= , 其中PF=PN,FH=2OF= . (1)、【基础训练】请分别直接写出抛物线y=的焦点坐标和准线l的方程: , ;(2)、【技能训练】如图2,已知抛物线y=上一点P(x0 , y0)(x0>0)到焦点F的距离是它到x轴距离的3倍,求点P的坐标;(3)、【能力提升】如图3,已知抛物线y=的焦点为F,准线方程为l.直线m:y=交y轴于点C,抛物线上动点P到x轴的距离为d1 , 到直线m的距离为d2 , 请直接写出d1+d2的最小值;(4)、【拓展延伸】该兴趣小组继续探究还发现:若将抛物线y=ax2(a>0)平移至y=a(x-h)2+k(a>0).
(1)、【基础训练】请分别直接写出抛物线y=的焦点坐标和准线l的方程: , ;(2)、【技能训练】如图2,已知抛物线y=上一点P(x0 , y0)(x0>0)到焦点F的距离是它到x轴距离的3倍,求点P的坐标;(3)、【能力提升】如图3,已知抛物线y=的焦点为F,准线方程为l.直线m:y=交y轴于点C,抛物线上动点P到x轴的距离为d1 , 到直线m的距离为d2 , 请直接写出d1+d2的最小值;(4)、【拓展延伸】该兴趣小组继续探究还发现:若将抛物线y=ax2(a>0)平移至y=a(x-h)2+k(a>0).抛物线y=a(x-h)2+k(a>0)内有一定点F(h,),直线l过点M(h,)且与x轴平行.当动点P在该抛物线上运动时,点P到直线l的距离PP1始终等于点P到点F的距离(该结论不需要证明).例如:抛物线y=2(x-1)2+3上的动点P到点F(1,)的距离等于点P到直线l:y=的距离.
请阅读上面的材料,探究下题:
如图4,点D(-1,)是第二象限内一定点,点P是抛物线y=-1上一动点.当PO+PD取最小值时,请求出△POD的面积.
六、综合题
-
36. 如图1,在平面直角坐标系中,已知抛物线与轴交于点 , 与轴交于点 , 顶点为 , 连接 .
 (1)、抛物线的解析式为;(直接写出结果)(2)、在图1中,连接并延长交的延长线于点 , 求的度数;(3)、如图2,若动直线与抛物线交于两点(直线与不重合),连接 , 直线与交于点 . 当时,点的横坐标是否为定值,请说明理由.37. 如图,等腰内接于 , , 是边上的中线,过点作的平行线交的延长线于点 , 交于点 , 连接 .
(1)、抛物线的解析式为;(直接写出结果)(2)、在图1中,连接并延长交的延长线于点 , 求的度数;(3)、如图2,若动直线与抛物线交于两点(直线与不重合),连接 , 直线与交于点 . 当时,点的横坐标是否为定值,请说明理由.37. 如图,等腰内接于 , , 是边上的中线,过点作的平行线交的延长线于点 , 交于点 , 连接 . (1)、求证:为的切线;(2)、若的半径为 , , 求的长.38. 如图1,点P是线段AB上与点A,点B不重合的任意一点,在AB的同侧分别以A,P,B为顶点作 ∠1=∠2=∠3,其中∠1与∠3的一边分别是射线AB和射线BA,∠2的两边不在直线AB上,我们规定这三个角互为等联角,点P为等联点,线段AB为等联线.
(1)、求证:为的切线;(2)、若的半径为 , , 求的长.38. 如图1,点P是线段AB上与点A,点B不重合的任意一点,在AB的同侧分别以A,P,B为顶点作 ∠1=∠2=∠3,其中∠1与∠3的一边分别是射线AB和射线BA,∠2的两边不在直线AB上,我们规定这三个角互为等联角,点P为等联点,线段AB为等联线.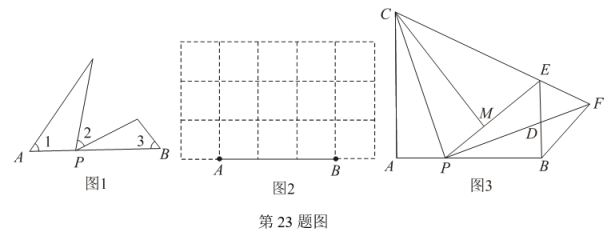 (1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.
(1)、如图2,在5×3个方格的纸上,小正方形的顶点为格点、边长均为1,AB为端点在格点的已知线段.请用三种不同连接格点的方法,作出以线段AB为等联线、某格点P为等联点的等联角,并标出等联角,保留作图痕迹;(2)、如图3,在Rt△APC中,∠A=90°, , 延长AP至点B,使AB=AC,作∠A的等联角∠CPD和∠PBD.将△APC沿PC折叠,使点A落在点M处,得到△MPC,再延长PM交BD的延长线于E,连接CE并延长交PD的延长线于F,连接BF.①确定△PCF的形状,并说明理由;
②若AP:PB=1:2,BF=k,求等联线AB和线段PE的长(用含k的式子表示).
39. 已知抛物线过点和点 , 与轴交于点 . (1)、求抛物线的解析式;(2)、如图1,连接 , 点在线段上(与点不重合),点是的中点,连接 , 过点作交于点 , 连接 , 当面积是面积的3倍时,求点的坐标;(3)、如图2,点是抛物线上对称轴右侧的点,是轴正半轴上的动点,若线段上存在点(与点不重合),使得 , 求的取值范围.40. 如图1,平面直角坐标系中,抛物线过点 , 和 , 连接 , 点为抛物线上一动点,过点作轴交直线于点 , 交轴于点 .
(1)、求抛物线的解析式;(2)、如图1,连接 , 点在线段上(与点不重合),点是的中点,连接 , 过点作交于点 , 连接 , 当面积是面积的3倍时,求点的坐标;(3)、如图2,点是抛物线上对称轴右侧的点,是轴正半轴上的动点,若线段上存在点(与点不重合),使得 , 求的取值范围.40. 如图1,平面直角坐标系中,抛物线过点 , 和 , 连接 , 点为抛物线上一动点,过点作轴交直线于点 , 交轴于点 . (1)、直接写出抛物线和直线的解析式;(2)、如图2,连接 , 当为等腰三角形时,求的值;(3)、当点在运动过程中,在轴上是否存在点 , 使得以 , , 为顶点的三角形与以 , , 为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.
(1)、直接写出抛物线和直线的解析式;(2)、如图2,连接 , 当为等腰三角形时,求的值;(3)、当点在运动过程中,在轴上是否存在点 , 使得以 , , 为顶点的三角形与以 , , 为顶点的三角形相似(其中点与点相对应),若存在,直接写出点和点的坐标;若不存在,请说明理由.