浙江省台州市仙居县2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-11 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分．各题中只有一个符合题意的正确选项，不选、多选、错选，均不给分）

1. $- 3$ 的绝对值是（）．

A、 $\frac{1}{3}$ B、3 C、 $- 3$ D、 $- \frac{1}{3}$

查看试题解析
2. 若用5表示向上移动5米，则向下移动2米记作（）．

A、 $- 2$ B、 $+ 2$ C、 $- \frac{1}{2}$ D、 $+ \frac{1}{2}$

查看试题解析
3. 下列关于单项式 $- \frac{2 a b^{2}}{3}$ 的说法中，正确的是（）

A、系数是 $\frac{2}{3}$ ，次数是3 B、系数是 $- \frac{2}{3}$ ，次数是2 C、系数是 $- \frac{2}{3}$ ，次数是3 D、系数是 $\frac{2}{3}$ ，次数是2

查看试题解析
4. 下列计算正确的是（）．

A、 ${(- \frac{1}{2})}^{3} = \frac{1}{8}$ B、 $(- 1)^{3} - (- 2)^{2} = - 3$ C、 $x + y = x y$ D、 $a^{2} b - 2 b a^{2} = - a^{2} b$

查看试题解析
5. 如图是一个正方体的展开图，把展开图折叠成正方体后，与“育”字一面相对的面上的字是（）．

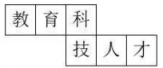A、人 B、教 C、才 D、技

查看试题解析
6. 下列根据等式性质的变形中，错误的是（）．

A、若 $\frac{x}{a} = \frac{y}{a}$ ，则 $x = y$ B、若 $x = y$ ，则 $a x - c = a y - c$ C、若 $x - a = y - a$ ，则 $x = y$ D、若 $c x = c y$ ，则 $x = y$

查看试题解析
7. 若 $A = x^{2} y + 2 x + 3 ， B = - 2 x^{2} y + 4 x$ ，则 $2 A - B =$ （）．

A、3 B、6 C、 $4 x^{2} y + 6$ D、 $4 x^{2} y + 3$

查看试题解析
8. 如图，点 $O$ 在直线 $A E$ 上， $∠ A O B = ∠ C O D = 90 °$ ，则图中除了直角外，一定相等的角有（）．

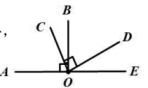A、3对 B、2对 C、1对 D、0对

查看试题解析
9. 有理数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（）

A、 $a b > 0$ B、 $b - a > 4$ C、 $\frac{a}{| a |} + \frac{b}{| b |} = 2$ D、 $(a + 2) (b - 3) < 0$

查看试题解析
10. 已知 $a_{1} = 3 ， a_{2} = \frac{1}{1 - a_{1}} ， a_{3} = \frac{1}{1 - a_{2}} ， a_{4} = \frac{1}{1 - a_{3}} ， \cdot \cdot \cdot$ ，依此类推，则 $a_{2024}$ 等于（）．

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、3

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 2021年6月3日，我国发射了“风云四号B卫星”，它运行在距离地面36000000米的地球同步轨道上，数36000000用科学记数法表示为．

查看试题解析
12. $36 ° 3 0^{'} =$ ．

查看试题解析
13. 若 $3 a - 2 b = 5$ ，则式子 $6 a - 4 b - 5$ 的值为．

查看试题解析
14. 为了大力弘扬亚运精神，某校特意举行了“扬帆起航，逐梦浙江”的知识竞赛，此次竞赛共20道选择题，且每题必答．评分标准如下：答对1题得5分，答错1题扣1分．已知小明的总分为82分，则他答对的题数是．

查看试题解析
15. 如图，两个正方形的一个顶点重合，且重合的顶点在一条直线上，那么 $∠ 1$ 的度数为．

查看试题解析
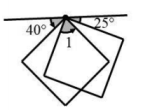16. 对于两个不相等的有理数 $a ， b$ ，我们规定符号 $m i n {a ， b}$ 表示 $a ， b$ 两数中较小的数，例如 $m i n {2 ， - 3} = - 3$ ．按照这个规定，方程 $m i n {x ， - x} = - 3 x - 12$ 的解为．

查看试题解析

三、解答题（本题有8小题，共66分；第17~18题每题6分，第19~22题每题8分，第23题10分，第24题12分）

17.

(1)、 $(- \frac{5}{12} + \frac{1}{6}) \times 24$ ；

(2)、 $- 1^{4} - \frac{1}{3} \times | 1 - (- 5)^{2} |$ ．

查看试题解析
18. 如图的数轴上，每小格的宽度相等．

(1)、填空：数轴上点 $A$ 表示的数是，点 $B$ 表示的数是．

(2)、点 $C$ 表示的数是 $- \frac{1}{3}$ ，点 $D$ 表示的数是 $- 1$ ，请在数轴上分别画出点 $C$ 和点 $D$ 的位置．

(3)、将 $A ， B ， C ， D$ 四个点所表示的数按从大到小的顺序排列，用“>”连接．

查看试题解析
19. 解方程 $\frac{2 x - 1}{3} = \frac{x - 2}{6} - 1$ ，并检验解出的结果是否正确．

查看试题解析
20. 如图，在平面内有不共线的三个点 $A ， B ， C$ ．

(1)、按下列要求作图：
分别作直线 $B C$ 、射线 $A B$ ，连接 $A C$ ．

(2)、思考：在线段 $B C$ 上任取一点 $D$ （不与点 $B 、 C$ 重合），连接 $A D$ ．
①若 $B C = a ， E 、 F$ 分别是线段 $B D$ 和 $D C$ 的中点．则线段 $E F$ 的长为 ▲ ；
②比较 $A C + B C$ 与 $A D + B D$ 的大小，并说明理由．

查看试题解析
21. 体育用品专卖店销售某款跳绳，原价5元一根，元旦期间八折优惠，学校用同样多的钱要比打折前多买了10根跳绳，问：学校在元旦期间购买了多少根跳绳？

查看试题解析
22. 将形状相同、大小相等的长方形A、B和形状相同，大小相等的长方形C、D按图摆放，拼成一个中间含正方形的大长方形．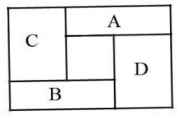

(1)、若长方形A的长为3，宽为1，设中间正方形的边长为x，用含x的式子表示拼成的大长方形的长和宽．

(2)、当长方形A的周长变化时，请写出拼成的大长方形的周长与长方形A的周长的关系，并说明理由．

查看试题解析
23. 已知：两块三角尺（直角三角形 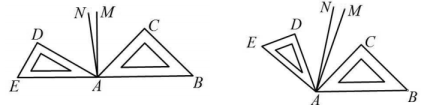$A B C$ 和直角三角形 $A D E ， ∠ B A C = 45 ° ， ∠ D A E = 30 °$ ）按如图1摆放，点 $E 、 A 、 B$ 在同一条直线上， $A M 、 A N$ 分别平分 $∠ B A E$ 和 $∠ C A D$ ．
图1 图2

(1)、求 $∠ D A C$ 的度数；

(2)、求 $∠ M A N$ 的度数；

(3)、将三角尺 $A D E$ 绕点 $A$ 按顺时针方向转动至如图2的位置，在转动过程中， $∠ M A N$ 的度数是否发生变化？如果不变化，请求出 $∠ M A N$ 的度数；如果变化，请说明理由．

查看试题解析
24. 台州西站到永康南站现有一条设计时速为 $160 k m$ 的单轨普速铁路．客车以 $150 k m / h$ 的平均速度行驶，从“铁路12306”可查得它在各站点的到达时间和驶出时间如下表：
到达站点
临海南
仙居南
磐安南
壶镇
永康南
到达时间
$11 ： 03$
$11 ： 25$
$11 ： 53$
$12 ： 04$
$12 ： 23$
驶出时间
$11 ： 05$
$11 ： 27$
$11 ： 55$
$12 ： 07$

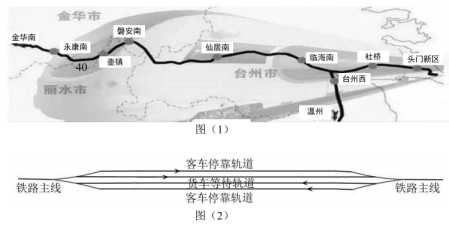(1)、求临海南、仙居南、磐安南、壶镇相邻两站之间的铁路公里数，并标注在下面相应的铁路示意图上．例如永康南与壶镇两站的公里数为40km，标记40．（只要求写数字，单位为km）．

(2)、一列货运列车以120km/h的速度匀速行驶开往永康南站，在10：55通过临海南站．
①若货运列车中途不停靠站点进行避让，它在到达永康南站前与客车有追尾危险吗？如果有追尾危险，请确定在它驶离临海南站多少千米时会追尾．
②为了确保列车运行安全，货运列车需要在客运列车追上前进入火车站，停靠在货车等待轨道等待客运列车通过（如图2）．请问：该货运列车应该停靠在哪个火车站等待客运列车通过才能使等待的时间最少？并求出停靠等待的时间（精确到1分钟）．

查看试题解析

到达站点	临海南	仙居南	磐安南	壶镇	永康南
到达时间	$11 ： 03$	$11 ： 25$	$11 ： 53$	$12 ： 04$	$12 ： 23$
驶出时间	$11 ： 05$	$11 ： 27$	$11 ： 55$	$12 ： 07$