浙江省嘉兴市2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-11 类型:期末考试
一、选择题(每小题有4个选项,其中有且只有一个正确,请把正确选项的编码填入答题卷的相应空格,每小题3分,共30分)
-
1. 任意抛一枚质地均匀的硬币,落地后“正面朝上”这一事件是( )A、必然事件 B、确定事件 C、随机事件 D、不可能事件2. 已知 , 则的值为( )A、 B、 C、 D、33. 抛物线的顶点坐标为( )A、 B、 C、 D、4. 已知是线段上黄金分割点, , , 则的长为( )A、 B、 C、 D、5. 如图,内接于是的直径,若 , 则的度数为( )
 A、 B、 C、 D、6. 如图,在平面直角坐标系中,以坐标原点为位似中心,在轴右侧作放大2倍后的位似图形 , 若点的坐标为 , 则点的对应点的坐标为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,以坐标原点为位似中心,在轴右侧作放大2倍后的位似图形 , 若点的坐标为 , 则点的对应点的坐标为( ) A、 B、 C、 D、7. 如图,我国古代数学家赵爽使用的弦图是由四个全等的直角三角形构成的正方形 , 若 , , 在弦图区域内随机取点,则该点落在正方形区域内的概率为( )
A、 B、 C、 D、7. 如图,我国古代数学家赵爽使用的弦图是由四个全等的直角三角形构成的正方形 , 若 , , 在弦图区域内随机取点,则该点落在正方形区域内的概率为( ) A、 B、 C、 D、8. 如图,点是等边三角形的重心, , 是边上一点,当时,则的长为( )
A、 B、 C、 D、8. 如图,点是等边三角形的重心, , 是边上一点,当时,则的长为( ) A、1 B、 C、 D、29. 如图,是一条弦,将劣弧沿弦翻折,连结并延长交翻折后的弧于点 , 连结 , 若 , 则的长为( )
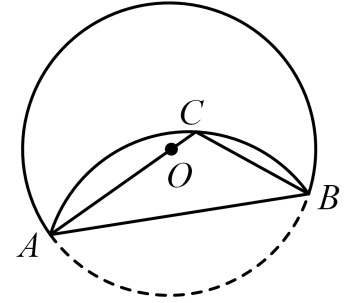
A、1 B、 C、 D、29. 如图,是一条弦,将劣弧沿弦翻折,连结并延长交翻折后的弧于点 , 连结 , 若 , 则的长为( )
 A、 B、 C、 D、10. 已知二次函数 , 当时,函数有最小值 , 则b的值为( )A、或 B、或 C、 D、或
A、 B、 C、 D、10. 已知二次函数 , 当时,函数有最小值 , 则b的值为( )A、或 B、或 C、 D、或二、填空题(本题有6小题,每小题3分,共18分)
-
11. 已知正n边形的一个外角是 , 则 .12. 如图,与交于点 , 连结和 , 要使 , 请添加一个条件: .
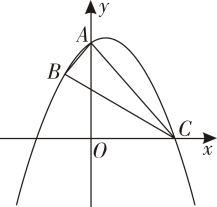
 13. 一个不透明的箱子里有3个球,其中2个白球,1个红球,它们除了颜色外其他都相同,从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则摸出的两个球恰好颜色不同的概率为 .14. 某车的刹车距离与开始刹车时的速度满足二次函数 , 若该车某次的刹车距离为 , 则开始刹车时的速度为 .15. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点 , 过点作轴的平行线交抛物线于点 , 抛物线顶点为 . 若直线交直线于点 , 且 , 则的值为 .16. 如图,内接于 , 已知是直径, , , 点在直径上方的半圆上运动,连结交于点 , 则的最大值为 .
13. 一个不透明的箱子里有3个球,其中2个白球,1个红球,它们除了颜色外其他都相同,从中任意摸出一个球,记下颜色后放回,搅匀,再摸出一个球,则摸出的两个球恰好颜色不同的概率为 .14. 某车的刹车距离与开始刹车时的速度满足二次函数 , 若该车某次的刹车距离为 , 则开始刹车时的速度为 .15. 在平面直角坐标系中,为坐标原点,抛物线与轴交于点 , 过点作轴的平行线交抛物线于点 , 抛物线顶点为 . 若直线交直线于点 , 且 , 则的值为 .16. 如图,内接于 , 已知是直径, , , 点在直径上方的半圆上运动,连结交于点 , 则的最大值为 .
三、解答题(本题有8小题,第17~22题每题6分,第23、24题每题8分,共52分)
-
17. 已知二次函数的图象经过点 .(1)、求的值;(2)、判断是否在该函数的图象上,并说明理由.18. 现有三张正面分别写有1,2,3的不透明卡片,卡片除正面数字外,其余均相同,将三张卡片正面向下洗匀.(1)、从中随机抽取一张卡片,求抽取写有1的卡片的概率;(2)、从中随机抽取两张卡片,求抽取的两张卡片上的数字之和为偶数的概率,用列表法或画树状图的方法加以说明.19. 如图,方格纸上每个小正方形的边长均为1个单位长度,点在格点上.
 (1)、画出过三点的圆的圆心;(2)、求的长.20. 如图,屋架跨度的一半 , 高度 . 现要在屋顶上开一个天窗,在水平位置,且 . 求天窗高度的长.
(1)、画出过三点的圆的圆心;(2)、求的长.20. 如图,屋架跨度的一半 , 高度 . 现要在屋顶上开一个天窗,在水平位置,且 . 求天窗高度的长. 21. 如图,水平放置的圆柱形排水管的截面半径为 , 截面中有水部分弓形的高为 .
21. 如图,水平放置的圆柱形排水管的截面半径为 , 截面中有水部分弓形的高为 . (1)、求截面中弦的长;(2)、求截面中有水部分弓形的面积.22. 根据以下素材,探索完成任务.
(1)、求截面中弦的长;(2)、求截面中有水部分弓形的面积.22. 根据以下素材,探索完成任务.素材1
某学校一块劳动实践基地大棚的横截面如图所示,上部分的顶棚是抛物线形状,下部分是由两根立柱和组成,立柱高为 , 顶棚最高点距离地面是 , 的长为 .

素材2
为提高灌溉效率,学校在的中点处安装了一款可垂直升降的自动喷灌器 , 从喷水口喷出的水流可以看成抛物线,其形状与的图象相同, , 此时水流刚好喷到立柱的端点处.
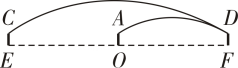
问题解决
任务1
确定顶棚的形状
以顶棚最高点为坐标原点建立平面直角坐标系,求出顶棚部分抛物线的表达式.
任务2
探索喷水的高度
问处喷出的水流在距离点水平距离为多少米时达到最高.
任务3
调整喷头的高度
如何调整喷水口的高度(形状不变),使水流喷灌时恰好落在边缘处.