浙江省宁波市鄞州区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-11 类型:期末考试
一、选择题(每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求)
-
1. 已知的半径为4,P为内一点,则OP的长度可能是( )A、3 B、4 C、5 D、92. 下列事件中,属于必然事件的是( )A、射击运动员射击一次恰好命中靶心 B、从一副完整的扑克牌中任抽一张,出现红桃A C、抛掷骰子两次,出现数字之和为13 D、观察正常的交通信号灯变化10分钟,看到绿灯3. 已知线段 , 点C是线段AB的黄金分割点,且 , 则线段AC的长是( )A、 B、 C、 D、4. 四边形ABCD内接于 , , 则的度数是( )A、 B、 C、 D、5. 如图,是的内切圆,AB,AC分别与相切于D,E两点,已知 , , 则的周长为( )
 A、14 B、 C、16 D、186. 已知 , , 三点都在抛物线上,则、、的大小关系为( )A、 B、 C、 D、7. 如图,的半径为5,弦 , 点C在弦AB上,延长CO交于点D,则CD的取值范围是( )
A、14 B、 C、16 D、186. 已知 , , 三点都在抛物线上,则、、的大小关系为( )A、 B、 C、 D、7. 如图,的半径为5,弦 , 点C在弦AB上,延长CO交于点D,则CD的取值范围是( )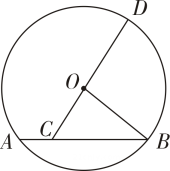 A、 B、 C、 D、8. 如图,点G是的重心,过点G作分别交AB,AC于点M,N,过点N作交BC于点D,则四边形BDNM与的面积之比是( )
A、 B、 C、 D、8. 如图,点G是的重心,过点G作分别交AB,AC于点M,N,过点N作交BC于点D,则四边形BDNM与的面积之比是( ) A、 B、 C、 D、9. 如图是由边长为1的小正方形组成的网格,的顶点及点M,N都是格点,AB与格线CN相交于点D,AC与MN相交于点E,则以下说法错误的是( )
A、 B、 C、 D、9. 如图是由边长为1的小正方形组成的网格,的顶点及点M,N都是格点,AB与格线CN相交于点D,AC与MN相交于点E,则以下说法错误的是( ) A、 B、 C、 D、10. 如图,正的边长为1,点P从点B出发,沿方向运动,于点H,下面是的面积随着点P的运动形成的函数图象(拐点左右两段都是抛物线的一部分),以下判断正确的是( )
A、 B、 C、 D、10. 如图,正的边长为1,点P从点B出发,沿方向运动,于点H,下面是的面积随着点P的运动形成的函数图象(拐点左右两段都是抛物线的一部分),以下判断正确的是( )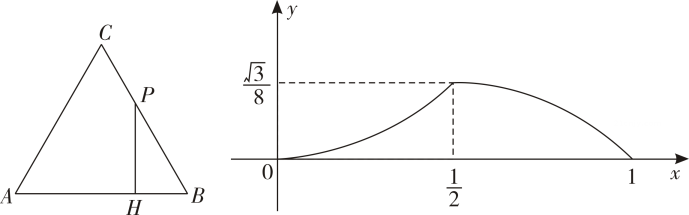 A、函数图象的横轴表示PB的长 B、当点P为BC中点时,点H为线段AB的三等分点 C、两段抛物线的形状不同 D、图象上点的横坐标为时,纵坐标为
A、函数图象的横轴表示PB的长 B、当点P为BC中点时,点H为线段AB的三等分点 C、两段抛物线的形状不同 D、图象上点的横坐标为时,纵坐标为二、填空题(每小题4分,共24分)
-
11. 在平面直角坐标系中,抛物线的开口方向是 .12. 一个布袋里装有3个红球、3个黄球和4个绿球,除颜色外其它都相同,搅匀后,随机摸出一个球是红球的概率为 .13. 的两个锐角和满足 , 则的度数是 .14. 如图,矩形ABCD被分割为3个面积相等的小矩形,已知矩形AFED与原矩形ABCD相似,则原矩形的较长边与较短边的比值是 .
 15. 如图1是杭州第19届亚运会会徽一“潮涌”,其主体为图2中的扇环.延长CA,DB交于点O, , 若 , , 则图2中扇环的面积为(结果保留)
15. 如图1是杭州第19届亚运会会徽一“潮涌”,其主体为图2中的扇环.延长CA,DB交于点O, , 若 , , 则图2中扇环的面积为(结果保留) 16. 如图,中, , , , CE是斜边AB上的中线,在直线AB上方作 , DE,FE分别与AC边交于点M,N,当与相似时,线段CN长度为 .
16. 如图,中, , , , CE是斜边AB上的中线,在直线AB上方作 , DE,FE分别与AC边交于点M,N,当与相似时,线段CN长度为 .
三、解答题(17~19题各6分,20~21题各8分,22~23题各10分,24题12分,共66分)
-
17.(1)、计算:;(2)、已知 , 求的值.18. 某校团委决定组织部分学生参加主题研学活动,全校每班可推选2名代表参加,901班根据各方面考核,决定从甲、乙、丙、丁四名学生中随机抽取两名参与研学活动.(1)、若甲已抽中,求从剩余3名学生中抽中乙参与研学的概率;(2)、用画树状图或列表等适当的方法求甲和乙同时参与研学的概率.19. 在如图所示的平面直角坐标系中,的顶点都在格点上,以原点O为位似中心,将放大到2倍得到 .
 (1)、在现有网格图中画出;(2)、记线段BC的中点为M,求放大后点M的对应点的坐标.20. 如图1,沙滩排球比赛中,裁判垂直站在记录台上.如图2是从正面看到的示意图,记录台底部O与垂直地面的球网支架底座E,F在同一水平线上,记录台与左侧球网距离OE为0.5m,裁判观察矩形球网ABCD上点A的俯角为42°,已知球网高度AE为2.4m.
(1)、在现有网格图中画出;(2)、记线段BC的中点为M,求放大后点M的对应点的坐标.20. 如图1,沙滩排球比赛中,裁判垂直站在记录台上.如图2是从正面看到的示意图,记录台底部O与垂直地面的球网支架底座E,F在同一水平线上,记录台与左侧球网距离OE为0.5m,裁判观察矩形球网ABCD上点A的俯角为42°,已知球网高度AE为2.4m.(本题参考数值 , , . )
 (1)、求裁判员眼睛距离地面的高度PO;(2)、某次运动员扣球后,球恰好从球网上边缘AD的点Q处穿过,此时裁判员的视线PQ正好看不到球网边界C处(即P,Q,C共线),若球网长度 , 球网下边缘离地面的距离CF为1.5m,求排球落点处Q离球网边界CD的距离.(结果精确到0.1m)21. 如图,AB为的直径,点P为BA延长线上一点,以点P为圆心,PO为半径画弧,以点O为圆心,AB为半径画弧,两弧相交于点C,连结OC交于点D,连结PD.
(1)、求裁判员眼睛距离地面的高度PO;(2)、某次运动员扣球后,球恰好从球网上边缘AD的点Q处穿过,此时裁判员的视线PQ正好看不到球网边界C处(即P,Q,C共线),若球网长度 , 球网下边缘离地面的距离CF为1.5m,求排球落点处Q离球网边界CD的距离.(结果精确到0.1m)21. 如图,AB为的直径,点P为BA延长线上一点,以点P为圆心,PO为半径画弧,以点O为圆心,AB为半径画弧,两弧相交于点C,连结OC交于点D,连结PD.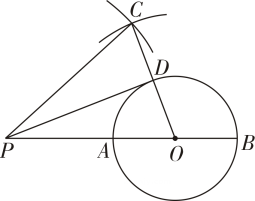 (1)、求证:PD与相切;(2)、若 , , 求的半径.22. 根据以下材料,探索完成任务:
(1)、求证:PD与相切;(2)、若 , , 求的半径.22. 根据以下材料,探索完成任务:智能浇灌系统使用方案
材料

如图1是一款智能浇灌系统,水管OP垂直于地面并可以随意调节高度(OP最大高度不超过2.4m),浇灌花木时,喷头P处会向四周喷射水流形成固定形状的抛物线,水流落地点M与点O的距离即为最大浇灌距离,各方向水流落地点形成一个以点O为圆心,OM为半径的圆形浇灌区域.
当喷头P位于地面与点O重合时,某一方向的水流上边缘形成了如图2的抛物线,经测量, , 水流最高时距离地面0.1m.
如图3,农科院将该智能浇灌系统应用于一个长8m,宽6m的矩形试验田中,水管放置在矩形中心O处.
问题解决
任务1
确定水流形状
在图2中建立合适的平面直角坐标系,求抛物线的函数表达式.
任务2
探究浇灌最大区域
当调节水管OP的高度时,浇灌的圆形区域面积会发生变化,请你求出最大浇灌圆形区域面积.(结果保留)
任务3
解决具体问题
若要保证浇灌区域能完全覆盖矩形试验田,则水管OP至少需要调节到什么高度?
