浙江省宁波市江北区2023-2024学年八年级上学期期末联考数学试卷
试卷更新日期:2024-03-11 类型:期末考试
一、选择题(每小题3分,共30分)
-
1. 下列四个图形中,不是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组线段,不能组成三角形的是( )A、1,2,3 B、2,3,4 C、3,4,5 D、5,12,133. 由x<y能得到mx>my,则( )A、m>0 B、m≥0 C、m<0 D、m≤04. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=5,EC=2,则BC的长是( )
2. 下列各组线段,不能组成三角形的是( )A、1,2,3 B、2,3,4 C、3,4,5 D、5,12,133. 由x<y能得到mx>my,则( )A、m>0 B、m≥0 C、m<0 D、m≤04. 如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=5,EC=2,则BC的长是( ) A、6 B、7 C、8 D、95. 能说明命题:“若a>b,则ac≥bc”是假命题的反例是( )A、c=﹣1 B、c=0 C、c=2 D、c=m2(m为任意实数)6. 在下面四个命题是真命题的个数有( )(1)、互相垂直的两条线段一定相交;(2)有且只有一条直线垂直于已知直线;(3)两条直线被第三条直线所截,同位角相等;(4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.A、3个 B、2个 C、1个 D、0个7. 对于任意实数p、q,定义一种运算:p@q=p-q+pq,例如2@3=2-3+2×3.请根据上述定义解决问题:若关于x的不等式组有3个整数解,则m的取值范围为是 ( )A、-8≤m<-5 B、-8<m≤-5 C、-8≤m≤-5 D、-8<m<-58. 一条直线y=kx+b,其中k+b= , kb= , 那么该直线经过( )A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限9. 某人骑自行车t(小时)走了 , 若步行 , 则比骑自行车多用3(小时),那么骑自行车每小时比步行多走( ) .A、 B、 C、 D、10. 如图,把一个大长方形分割成5小块,其中⑤号是正方形,其余都是长方形,且①号和④号是两个一样的长方形,⑤号的周长是①号的2倍.已知大的长方形的面积,可以求出下列哪一个图形的面积.( )
A、6 B、7 C、8 D、95. 能说明命题:“若a>b,则ac≥bc”是假命题的反例是( )A、c=﹣1 B、c=0 C、c=2 D、c=m2(m为任意实数)6. 在下面四个命题是真命题的个数有( )(1)、互相垂直的两条线段一定相交;(2)有且只有一条直线垂直于已知直线;(3)两条直线被第三条直线所截,同位角相等;(4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.A、3个 B、2个 C、1个 D、0个7. 对于任意实数p、q,定义一种运算:p@q=p-q+pq,例如2@3=2-3+2×3.请根据上述定义解决问题:若关于x的不等式组有3个整数解,则m的取值范围为是 ( )A、-8≤m<-5 B、-8<m≤-5 C、-8≤m≤-5 D、-8<m<-58. 一条直线y=kx+b,其中k+b= , kb= , 那么该直线经过( )A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限9. 某人骑自行车t(小时)走了 , 若步行 , 则比骑自行车多用3(小时),那么骑自行车每小时比步行多走( ) .A、 B、 C、 D、10. 如图,把一个大长方形分割成5小块,其中⑤号是正方形,其余都是长方形,且①号和④号是两个一样的长方形,⑤号的周长是①号的2倍.已知大的长方形的面积,可以求出下列哪一个图形的面积.( ) A、① B、② C、③ D、⑤
A、① B、② C、③ D、⑤二、填空题(每小题3分,共18分)
-
11. 如图,活动衣架可以伸缩自如,是利用了四边形的 性质.
 12. 如图,直角坐标系中,已知A(-2,-1),B(3,-1),C(1,2),请你在y轴上找一点P.使 ABP和 ABC全等,则点P的坐标是 . (写出一个即可)
12. 如图,直角坐标系中,已知A(-2,-1),B(3,-1),C(1,2),请你在y轴上找一点P.使 ABP和 ABC全等,则点P的坐标是 . (写出一个即可) 13. 如图,正比例函数和一次函数的图象相交于点 , 当时,(填“>”或“<”)
13. 如图,正比例函数和一次函数的图象相交于点 , 当时,(填“>”或“<”) 14. 已知中,斜边 , 则斜边上的中线的长为 .15. 如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点于 ,且 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,…,按此规律进行下去,则点 的横坐标是.
14. 已知中,斜边 , 则斜边上的中线的长为 .15. 如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点于 ,且 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,…,按此规律进行下去,则点 的横坐标是.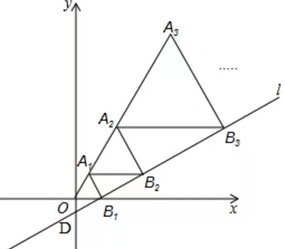 16. 如图1,在 中, , 为 中点.将 沿 翻折,得到 (如图2), 为 上一点,再将 沿 翻折,使得 与 重合(如图3),给出下列四个命题:① ;② ;③ ;④ .其中说法正确的是.
16. 如图1,在 中, , 为 中点.将 沿 翻折,得到 (如图2), 为 上一点,再将 沿 翻折,使得 与 重合(如图3),给出下列四个命题:① ;② ;③ ;④ .其中说法正确的是.


三、解答题(第17~19题每题6分,第20~21每题8分,第22~23题每题9分,共52分)
-
17. 解方程组或解不等式组.(1)、解方程组:(2)、解不等式组: , 并把解集在数轴上表示出来.
 18. 如图, , , , , 垂足分别是 , .
18. 如图, , , , , 垂足分别是 , . (1)、求证:;(2)、猜想线段 , , 之间具有怎样的数量关系,并说明理由.19. 如图,在每个小正方形的边长均为1的方格纸中有线段AB,其中点A、B均在小正方形的顶点上.
(1)、求证:;(2)、猜想线段 , , 之间具有怎样的数量关系,并说明理由.19. 如图,在每个小正方形的边长均为1的方格纸中有线段AB,其中点A、B均在小正方形的顶点上. (1)、在方格纸中画出以BC为底的钝角等腰三角形ABC,且点C在小正方形的顶点上;(2)、将(1)中的△ABC绕点C逆时针旋转90°得到△DEC点A的对应点是点D,点B的对应点是点E),画出△CDE;(3)、在(2)的条件下,连接BE,请直接写出△BCE的面积.20. 如图1,在平面直角坐标系中,正方形的面积等于4,长方形的面积等于8,其中点、在轴上,点在轴上.
(1)、在方格纸中画出以BC为底的钝角等腰三角形ABC,且点C在小正方形的顶点上;(2)、将(1)中的△ABC绕点C逆时针旋转90°得到△DEC点A的对应点是点D,点B的对应点是点E),画出△CDE;(3)、在(2)的条件下,连接BE,请直接写出△BCE的面积.20. 如图1,在平面直角坐标系中,正方形的面积等于4,长方形的面积等于8,其中点、在轴上,点在轴上. (1)、请直接写出点 , 点 , 点的坐标;(2)、如图2,将正方形沿轴向右平移,移动后得到正方形 , 设移动后的正方形长方形重叠部分(图中阴影部分)的面积为;
(1)、请直接写出点 , 点 , 点的坐标;(2)、如图2,将正方形沿轴向右平移,移动后得到正方形 , 设移动后的正方形长方形重叠部分(图中阴影部分)的面积为;①当时, ▲ ;当时, ▲ ;当时, ▲ ;
②当时,请直接写出的值.
21. 某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费120元,购进A品牌文具袋3个和B品牌文具袋4个共花费88元.(1)、求购进A品牌文具袋和B品牌文具袋的单价;(2)、若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为w元.①求w关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不低于进货价格的45%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
22. 如图,两个形状,大小完全相同的含有30°,60°的三角板如图①放置,PA,PB与直线MN重合,且三角板PAC与三角板PBD均可绕点P逆时针旋转。 (1)、试说明:∠DPC=90°;(2)、如图②,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定度数,PF平分 ,PE平分 ,求 。(3)、如图③,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3/s。同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2/s,在两个三角板旋转过程中(PC转到与PM重合时,三角板都停止转运),问 的值是否变化?若不变,求出其值,若变化,说明理由。23. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于A , B两点,把线段AB绕点B顺时针旋转后得到线段BC , 连结AC , OC.
(1)、试说明:∠DPC=90°;(2)、如图②,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定度数,PF平分 ,PE平分 ,求 。(3)、如图③,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3/s。同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2/s,在两个三角板旋转过程中(PC转到与PM重合时,三角板都停止转运),问 的值是否变化?若不变,求出其值,若变化,说明理由。23. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于A , B两点,把线段AB绕点B顺时针旋转后得到线段BC , 连结AC , OC.
 (1)、当时,求点C的坐标;(2)、当m值发生变化时,△BOC的面积是否保持不变?若不变,计算其大小;若变化,请说明理由;(3)、当S△AOB=2S△BOC时,在x轴上找一点P , 使得△PAB是等腰三角形,求满足条件的所有P点的坐标.
(1)、当时,求点C的坐标;(2)、当m值发生变化时,△BOC的面积是否保持不变?若不变,计算其大小;若变化,请说明理由;(3)、当S△AOB=2S△BOC时,在x轴上找一点P , 使得△PAB是等腰三角形,求满足条件的所有P点的坐标.