浙江省瑞安市六校联盟2023-2024学年八上数学期末学业水平测试试题

试卷更新日期：2024-03-11 类型：期末考试

进入出卷网下载

一、选择题（每题4分，共48分）

1. 已知一次函数y=kx+3的图象经过点A ，且函数值y随x的增大而增大，则点A的坐标不可能是（）

A、（2，4） B、（－1，2） C、（5，1） D、（－1，－4）

查看试题解析
2. 若把分式 $\frac{3 x + 4 y}{2 x - 5 y}$ 中的 $x ， y$ 都扩大 $4$ 倍，则该分式的值（）

A、不变 B、扩大 $4$ 倍 C、缩小 $4$ 倍 D、扩大 $16$ 倍

查看试题解析
3. 下列四个实数中，无理数是（）

A、3.14 B、﹣π C、0 D、 $\sqrt{4}$

查看试题解析
4. 某文具超市有 $A ， B ， C ， D$ 四种水笔销售，它们的单价分别是5元，4元，3元，1.2元．某天的水笔销售情况如图所示，那么这天该文具超市销售的水笔的单价的平均值是（）

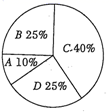A、4元 B、4.5元 C、3.2元 D、3元

查看试题解析
5. 已知：一组数据-1，2，-1，5，3，4，关于这组数据，下列说法错误的是（）

A、平均数是2 B、众数和中位数分别是-1和2.5 C、方差是16 D、标准差是 $\frac{4}{3} \sqrt{3}$

查看试题解析
6. 如图所示，直角三边形三边上的半圆面积从小到大依次记为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ，则 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 的关系是（　　）

A、 $S_{1} + S_{2} = S_{3}$ B、 ${S_{1}}^{2} + {S_{2}}^{2} = {S_{3}}^{2}$ C、 $S_{1} + S_{2} > S_{3}$ D、 $S_{1} + S_{2} < S_{3}$

查看试题解析
7. 如图，△ABC中，AB=6，AC=4，∠ABC和∠ACB的平分线交于点P，过点P作DE $/ /$ BC分别交AB，AC于点D，E，则△ADE的周长为（）

A、10 B、12 C、14 D、不能确定

查看试题解析
8. 人体中红细胞的直径约为0.000 007 7m，将数0.000 007 7用科学记数法表示为（）

A、7.7× $1 0^{- 5}$ B、 $0.77 \times 1 0^{- 7}$ C、 $7.7 \times 1 0^{- 6}$ D、 $7.7 \times 1 0^{- 7}$

查看试题解析
9. 如图，在平行四边形 $A B C D$ 中，延长 $C D$ 到 $E$ ，使 $D E = C D$ ，连接 $B E$ 交 $A D$ 于点 $F$ ，交 $A C$ 于点 $G$ ．下列结论① $D E = D F$ ；② $A G = G F$ ；③ $A F = D F$ ；④ $B G = G C$ ；⑤ $B F = E F$ ，其中正确的有（）个．

A、1 B、2 C、3 D、4

查看试题解析
10. 如果解关于x的分式方程 $\frac{2 x}{x - 3} - \frac{a}{3 - x}$ ＝5时出现了增根，那么a的值是（　　）

A、﹣6 B、﹣3 C、6 D、3

查看试题解析
11. 如果y=x-2a+1是正比例函数，则a的值是（）

A、 $\frac{1}{2}$ B、0 C、 $- \frac{1}{2}$ D、-2

查看试题解析
12. 一个三角形任意一边上的高都是这边上的中线，则对这个三角形最准确的判断是（）

A、等腰三角形 B、直角三角形 C、正三角形 D、等腰直角三角形

查看试题解析

二、填空题（每题4分，共24分）

13. 若a、b为实数，且b= $\frac{\sqrt{a^{2} - 1} + \sqrt{1 - a^{2}}}{a - 1}$ +4，则a+b的值为．

查看试题解析
14. 如图，在平面直角坐标系中，长方形OABC的顶点O在坐标原点，顶点A、C分别在x、y轴的正半轴上：OA＝3，OC＝4，D为OC边的中点，E是OA边上的一个动点，当△BDE的周长最小时，E点坐标为．

查看试题解析
15. 若 $P (- 3 ， 2)$ ，则点P到y轴的距离为.

查看试题解析
16. 如图，在平行四边形ABCD中，∠C=120°，AD=4，AB=2，点H、G分别是边CD、BC上的动点．连接AH、HG ，点E为AH的中点，点F为GH的中点，连接EF则EF的最大值与最小值的差为．

查看试题解析
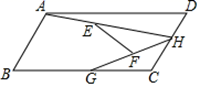17. 如图，已知△ABC，按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连结AD，CD．则△ABC≌△ADC的依据是．

查看试题解析
18. 2的相反数是．

查看试题解析

三、解答题（共78分）

19. 如图，正方形网格中每个小正方形的边长为1，格点△ABC的顶点A（2，3）、B（﹣1，2），将△ABC平移得到△A^'B^'C^' ，使得点A的对应点A^' ，请解答下列问题：

(1)、根据题意，在网格中建立平面直角坐标系；

(2)、画出△A^'B^'C^' ，并写出点C^'的坐标为 ▲ ．

查看试题解析
20. 如图，梯子长25米，斜靠在一面墙上，梯子底端离墙7米.

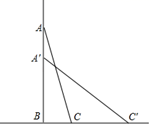(1)、这个梯子的顶端距地面有多高？

(2)、如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米？

查看试题解析
21. 如图，在平行四边形ABCD中， $∠$ BCD的平分线与BA的延长线相交于点E，求证：BE=BC．

查看试题解析
22. 探究活动：

(1)、如图①，可以求出阴影部分的面积是．（写成两数平方差的形式）

(2)、知识应用，运用你所得到的公式解决以下问题：
①计算： $(a + b - 2 c) (a + b + 2 c)$ ．
②若 $4 x^{2} - 9 y^{2} = 10$ ， $4 x + 6 y = 6$ ，求 $2 x - 3 y$ 的值．

查看试题解析
23. 计算：

(1)、（2x+1）²﹣（2x+5）（2x﹣5）

(2)、[2x（x²y²﹣xy）﹣y（x²﹣x³y）]÷3x²y

(3)、（﹣ $\frac{a^{2} b}{c}$ ）³•（﹣ $\frac{c^{2}}{a^{2}}$ ）²÷（﹣ $\frac{b c}{a}$ ）⁴

查看试题解析
24. “转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．

(1)、请你根据已经学过的知识求出下面星形图（1）中∠A+∠B+∠C+∠D+∠E的度数；

(2)、若对图（1）中星形截去一个角，如图（2），请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数；

(3)、若再对图（2）中的角进一步截去，你能由题（2）中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程）

查看试题解析
25. 如图，在平面直角坐标系中，A（-3，3），B（-4，-2），C（-1，-1）．

(1)、在图中作出△ABC关于y轴对称的△A＇B＇C＇，并写出点C＇的坐标 ▲ ；

(2)、在y轴上画出点P，使PA+PC最小，并直接写出P点坐标．

查看试题解析
26. 如图，由5个全等的正方形组成的图案，请按下列要求画图：

(1)、在图案（1）中添加1个正方形，使它成轴对称图形但不是中心对称图形．

(2)、在图案（2）中添加1个正方形，使它成中心对称图形但不是轴对称图形．

(3)、在图案（3）中添加1个正方形，使它既成轴对称图形，又成中心对称图形．

查看试题解析