浙江省绍兴市嵊州市崇仁片联2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-03-11 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. $- \frac{1}{2024}$ 的倒数是（）

A、 $\frac{1}{2024}$ B、2024 C、－2024 D、 $- \frac{1}{2024}$

查看试题解析
2. 若气温为零上20℃记作＋20℃，则－12℃表示气温为（）

A、零上8℃ B、零下8℃ C、零上12℃ D、零下12℃

查看试题解析
3. 餐桌边的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为（）

A、5×10¹⁰千克 B、50×10⁹千克 C、5×10⁹千克 D、0.5×10¹¹千克

查看试题解析
4. 在算式 $(- 2) □ (- 3)$ 的□中填上运算符号，使结果最小，运算符号是（）

A、加号 B、减号 C、乘号 D、除号

查看试题解析
5. “如图是一个正方形，把此正方形沿虚线AB减去一个角，得到一个五边形，则这个五边形的周长____原来正方形的周长，理由是____”此题中横线上应填写的正确答案是（）

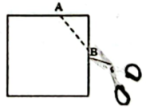A、大于，两点之间线段最短 B、小于，两点之间线段最短 C、大于，垂线段最短 D、小于，垂线段最短

查看试题解析
6. 在实数－3.14，0， $π$ ， $\frac{22}{7}$ ， $\sqrt[3]{9}$ ， 0.1010010001中无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 将一副三角尺按不同方式摆放，下列摆放方式中 $∠ α$ 与 $∠ β$ 一定相等的是（）

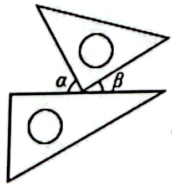A、 B、 C、 D、

查看试题解析
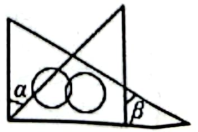8. 《九章算术》中记载了这样一个数学问题：今有甲发长安，五日至齐；乙发齐，七日至长安．今乙发已先二日，甲仍发长安．问几何日相逢？译文：甲从长安出发，5日到齐国；乙从齐国出发，7日到长安，现乙先出发2日，甲才从长安出发．问多久后甲乙相逢？设乙出发x日，甲乙相逢，则可列方程（）

A、 $\frac{x + 2}{7} + \frac{x}{5} = 1$ B、 $\frac{x - 2}{7} + \frac{x}{5} = 1$ C、 $\frac{x}{7} + \frac{x - 2}{7} = 1$ D、 $\frac{x}{7} + \frac{x - 2}{5} = 1$

查看试题解析
9. 如图，某长方形花园的长为 $(x + y)$ 米，宽为 $(x - y)$ 米，现根据实际需要对该花园进行整改，长方形花园的长增加 $(x - y)$ 米，宽增加 $(x - 2 y)$ 米，则整改后该花园的周长为（）

A、 $(4 x - 3 y)$ 米 B、 $(4 x - 6 y)$ 米 C、 $(8 x - 3 y)$ 米 D、 $(8 x - 6 y)$ 米

查看试题解析
10. 在多项式 $x - y - z - m - n$ （其中 $x > y > z > m > n$ ）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如 $x - y - | z - m | - n = x - y - z + m - n$ ， $| x - y | - z - | m - n | = x - y - z - m + n$ ， ……则所有“绝对操作”共有（）种不同运算结果

A、7 B、6 C、5 D、4

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 比较大小： $\sqrt{6}$ 3（填“＞”、“＝”或“＜”）．

查看试题解析
12. 单项式 $- 2 a b^{2}$ 的次数是次．

查看试题解析
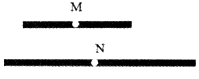
13. 若 $a - 3 b = - 5$ ，则 $2 {(a - 3 b)}^{2} + 3 b - a - 15 =$ ．

查看试题解析
14. 如图，两根木条的长度分别为7cm和12cm，在它们的中点处各打一个小孔M、N（木条的厚度，宽度以及小孔大小均忽略不计）．将这两根木条的一端重合并放置在同一条直线上，则两小孔间的距离MN＝cm．

查看试题解析
15. 多项式 $m x - n$ 和 $- 2 m x + n$ （m，n为实数，且 $m \neq 0$ ）的值随x的取值不同而不同，下表是当x取不同值时多项式对应的值，则关于x的方程 $- m x + n = 2 m x - n$ 的解是．
x
1
2
3
4
$m x - n$
－2
－1
0
1
$- 2 m x + n$
1
－1
－3
－5

查看试题解析
16. 将一张长方形的纸按如图对折，对折时每次折痕与上次的折痕保持平行，第一次对折后可得到1条折痕（图中虚线），第二次对折后可得到3条折痕，第三次对折后得到7条折痕，那么第7次对折后得到的折痕共有条．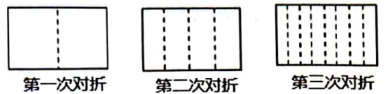

查看试题解析

三、解答题（本大题共8小题，共52分）

17. 计算：

(1)、 $- 3 + (- 5) - (- 8)$

(2)、 $\sqrt[3]{- 27} \times 2 - 6 \div (- \frac{2}{3})$

查看试题解析
18. 解方程：

(1)、 $2 (x - 3) = 3 x + 1$

(2)、 $\frac{2 x - 1}{3} = 1 - \frac{x + 1}{2}$

查看试题解析
19. 先化简再求值： $3 x - 2 (x^{2} - \frac{1}{2} y^{2}) + (x - \frac{1}{2} y^{2})$ ，其中 $x = 2$ ， $y = - 1$ ．

查看试题解析
20. 平面上有四个点M，N，E，F，按照以下要求作图（保留作图痕迹）：

(1)、连接MN，并延长MN至G，使 $N G = M N$ ；

(2)、作射线ME；

(3)、作直线MF，并在直线MF上确定点H，使得 $N H + H E$ 最短．

查看试题解析

21. 根据下面柔柔和小齐的对话，请计算小齐买平板电脑的预算．

柔柔：小齐，你之前提到的平板电脑买了没？

小齐：还没，它的售价比我的预算多1000元呢！

柔柔：这台平板电脑现在正在打7折呢！

小齐：是嘛，太好了，这样比我的预算还要少500元！

查看试题解析

22. 已知数轴上的点A和点B之间的距离为28个单位长度，点A在原点左边距离原点8个单位长度，点B在原点的右边．

(1)、请直接写出A，B两点所对应的数．

(2)、已知，数轴上点M从点A向左出发速度为每秒1个单位长度，同时点N从点B向左出发速度为每秒2个单位长度，经t秒后 $M O = N O$ ，求t的值．

查看试题解析
23. 如图，按程序框图中的顺序计算，当输出的最后结果为128时，求输入的初始值x，且x为正整数．

查看试题解析
24. 如果两个角之差的绝对值等于60°，则称这两个角互为等差角．即若 $| ∠ a - ∠ β | = 60 °$ ，则称 $∠ a$ 和 $∠ β$ 互为等差角．（本题中所有角都是指大于0°，且小于180°的角）

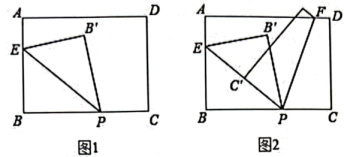(1)、若 $∠ 1$ 和 $∠ 2$ 互为等差角．当 $∠ 1 = 40 °$ ，则 $∠ 2 =$ ．当 $∠ 1 = 90 °$ ，则 $∠ 2 =$ ．

(2)、如图1，将一长方形纸片沿着EP对折（点P在线段BC上，点E在线段AB上）使点B落在点 $B^{'}$ 若 $∠ E P B^{'}$ 与 $∠ B^{'} P C$ 互为等差角，求 $∠ B P E$ 的度数．

(3)、再将纸片沿着FP对折（点F在线段CD或AD上）使点C落在点 $C^{'}$ ．如图2，若点E， $C^{'}$ ， P在同一直线上，且 $∠ B^{'} P C^{'}$ 与 $∠ E P F$ 互为等差角，求 $∠ E P F$ 的度数．（对折时，线段 $P B^{'}$ 落在 $∠ E P F$ 内部）

查看试题解析

x	1	2	3	4
$m x - n$	－2	－1	0	1
$- 2 m x + n$	1	－1	－3	－5