河南省信阳市淮滨县2023-2024学年下学期入学学情调研测试九年级数学试题
试卷更新日期:2024-03-11 类型:开学考试
一、单选题(每小题3分,共30分)
-
1. 下列四个数中,最小的数是( )A、﹣1 B、0 C、﹣ D、22. 2023年2月16日交通运输部发布信息,为期40天的春运于2月15日收官,全国营业性客运量约亿人次比2022年同期增长50.5%,数据“亿”用科学记数法可表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是几个相同的小立方块所搭的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则这个几何体的主视图是( )
 A、
A、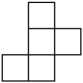 B、
B、 C、
C、 D、
D、 5. 如图,直线 , 若 , , 则的度数为( )
5. 如图,直线 , 若 , , 则的度数为( ) A、 B、 C、 D、6. 小明得到数学课外兴趣小组成员的年龄情况统计如下表,那么对于不同的值,则下列关于年龄的统计量不会发生变化的是( )
A、 B、 C、 D、6. 小明得到数学课外兴趣小组成员的年龄情况统计如下表,那么对于不同的值,则下列关于年龄的统计量不会发生变化的是( )年龄(岁)
13
14
15
16
人数(人)
2
15
A、平均数、方差 B、中位数、方差 C、平均数、中位数 D、众数、中位数7. 若事件“关于的一元二次方程有实数根”是必然事件,则的取值范围是( )A、 B、 C、且 D、且8. 明代程大位有一首类似二元一次方程组的饮酒数学诗,现进行了变式,大意是:好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒二位客人,如果29位客人醉倒了,他们总共饮下16瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒瓶,薄酒瓶。依题意,可列方程组为( ) A、 B、 C、 D、9. 如图,在中, . 按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交 , 于点 , ;②分别以 , 为圆心,大于的长为半径画弧,两弧在内交于点;③作射线 . 若 , 为边的中点,为射线上一动点,则的最小值为( )
A、 B、 C、 D、9. 如图,在中, . 按以下步骤作图:①以点为圆心,适当长为半径画弧,分别交 , 于点 , ;②分别以 , 为圆心,大于的长为半径画弧,两弧在内交于点;③作射线 . 若 , 为边的中点,为射线上一动点,则的最小值为( ) A、3 B、 C、 D、510. 在平面直角坐标系中,菱形的位置如图所示,其中点的坐标为 , 第1次将菱形绕着点顺时针旋转 , 同时扩大为原来的2倍得到菱形(即),第2次将菱形绕着点顺时针旋转 , 同时扩大为原来的2倍得到菱形(即),第3次将菱形绕着点顺时针旋转 , 同时扩大为原来的2倍得到菱形(即)…依次类推,则点的坐标为( )
A、3 B、 C、 D、510. 在平面直角坐标系中,菱形的位置如图所示,其中点的坐标为 , 第1次将菱形绕着点顺时针旋转 , 同时扩大为原来的2倍得到菱形(即),第2次将菱形绕着点顺时针旋转 , 同时扩大为原来的2倍得到菱形(即),第3次将菱形绕着点顺时针旋转 , 同时扩大为原来的2倍得到菱形(即)…依次类推,则点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共15分)
-
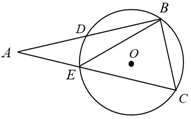
11. 请写出一个当时,随的增大而减小的函数表达式:。12. 不等式组 的最大整数解为.13. 将标有“中”“华”“崛”“起”的四个小球装在一个不透明的口袋中(每个小球上仅标一个汉字),这些小球除所标汉字不同外,其余均相同.从中随机摸出两个球,则摸到的球上的汉字可以组成“中华”的概率是 .14. 如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在 上,边AB、AC分别交 于D、E两点﹐点B是 的中点,则∠ABE=.
 15. 如图是一张菱形纸片, , , 点在边上,且 , 点在边上,把沿直线对折,点的对应点为点 , 当点落在菱形对角线上时,则。
15. 如图是一张菱形纸片, , , 点在边上,且 , 点在边上,把沿直线对折,点的对应点为点 , 当点落在菱形对角线上时,则。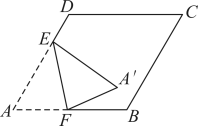
三、解答题(本大题共8题,共75分)
-
16.(1)、计算:;(2)、化简:17. 青春是校园生活的主旋律,某学校为了丰富学生的课余生活,焕发青春活力,激励学生成长,推动校园文化建设,开展了一次“美好青春,和谐校园”的校歌比赛,并在九(1)班和九(2)班各随机抽取了10名同学参加。
比赛成绩收集、整理如下:
九(1)班成绩:9 9.5 9 9 8 10 9 8 4 9.5
九(2)班成绩:
成绩
6
8
8.5
9
9.5
10
人数
2
1
3
1
2
1
比赛成绩分析:
平均数
中位数
众数
九(1)班
8.5
9
c
九(2)班
a
b
8.5
根据以上信息,同答下列问题:
(1)、填空: , , ;(2)、如果你是评委,请根据以上数据,判断两个班中哪个班的校歌歌唱水平比较好?并说明理由。18. 如图,在中, , 点O为边上一点,以为半径的与相切于点D,分别交边于点E,F。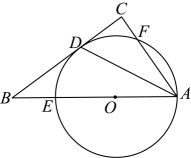 (1)、求证:平分;(2)、若 , 求的长。19. 如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm。
(1)、求证:平分;(2)、若 , 求的长。19. 如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm。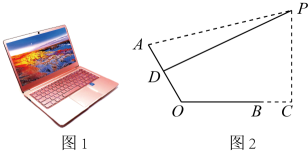 (1)、当PA=45cm时,求PC的长;(2)、若∠AOC=120°,求PC的长.(结果精确到0.1cm,参考数据:≈1.414,≈1.732)20. 2022年4月16日,神舟十三号载人飞船返回舱成功着陆,三名航天员平安归来,神舟十三号任务取得圆满成功.飞箭航模店看准商机,推出了“神舟”和“天宫”模型。已知每个“神舟”模型的成本比“天宫”模型多10元,同样花费100元,购进“天宫”模型的数量比“神舟”模型多5个。
(1)、当PA=45cm时,求PC的长;(2)、若∠AOC=120°,求PC的长.(结果精确到0.1cm,参考数据:≈1.414,≈1.732)20. 2022年4月16日,神舟十三号载人飞船返回舱成功着陆,三名航天员平安归来,神舟十三号任务取得圆满成功.飞箭航模店看准商机,推出了“神舟”和“天宫”模型。已知每个“神舟”模型的成本比“天宫”模型多10元,同样花费100元,购进“天宫”模型的数量比“神舟”模型多5个。 (1)、“神舟”和“天宫”模型的成本各多少元?(2)、飞箭航模店计划购买两种模型共200个,且每个“神舟”模型的售价为30元,“天宫”模型的售价为15元.设购买“神舟”模型个,销售这批模型的利润为元。
(1)、“神舟”和“天宫”模型的成本各多少元?(2)、飞箭航模店计划购买两种模型共200个,且每个“神舟”模型的售价为30元,“天宫”模型的售价为15元.设购买“神舟”模型个,销售这批模型的利润为元。①求与的函数关系式(不要求写出的取值范围);
②若购进“神舟”模型的数量不超过“天宫”模型数量的 , 则购进“神舟”模型多少个时,销售这批模型可以获得最大利润?最大利润是多少?
21. 如图,反比例函数的图象与一次函数的图象交于第二象限的点、点 , 与轴交于点 , 其中点的坐标为 , 点的到轴的距离为 . (1)、试确定反比例函数的关系式;(2)、请用无刻度的直尺和圆规作出点关于直线的对称点(要求:不写作法,保留作图痕迹);(3)、点 , , 与(2)中的点 , 组成四边形 . 求证:四边形是菱形。22. 在平面直角坐标系中,二次函数的图象与一次函数的图象交于点和点B,点B为二次函数图象的顶点。
(1)、试确定反比例函数的关系式;(2)、请用无刻度的直尺和圆规作出点关于直线的对称点(要求:不写作法,保留作图痕迹);(3)、点 , , 与(2)中的点 , 组成四边形 . 求证:四边形是菱形。22. 在平面直角坐标系中,二次函数的图象与一次函数的图象交于点和点B,点B为二次函数图象的顶点。 (1)、求二次函数和一次函数的解析式;(2)、结合图象直接写出不等式的解集;(3)、点M为二次函数图象上的一个动点,且点M的横坐标为m,将点M向右平移1个单位长度得到点N.若线段与一次函数图象有交点,直接写出点M横坐标m的取值范围。23. 已知点C为和的公共顶点,将绕点C顺时针旋转 , 连接 , , 请完成如下问题:
(1)、求二次函数和一次函数的解析式;(2)、结合图象直接写出不等式的解集;(3)、点M为二次函数图象上的一个动点,且点M的横坐标为m,将点M向右平移1个单位长度得到点N.若线段与一次函数图象有交点,直接写出点M横坐标m的取值范围。23. 已知点C为和的公共顶点,将绕点C顺时针旋转 , 连接 , , 请完成如下问题: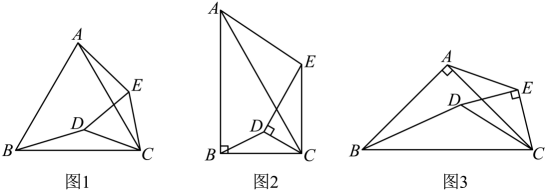 (1)、如图1,若和均为等边三角形,①线段与线段的数量关系是;②直线与直线相交所夹锐角的度数是;
(1)、如图1,若和均为等边三角形,①线段与线段的数量关系是;②直线与直线相交所夹锐角的度数是;类比探究:
(2)、如图2,若 , , 其他条件不变,则(1)中的结论是否都成立?请说明理由;(3)、拓展应用:如图3,若 , , , , 当点B,D,E三点共线时,请直接写出的长.