黑龙江省哈尔滨市重点学校2023-2024学年九年级下学期开学考试数学试题
试卷更新日期:2024-03-11 类型:开学考试
一、选择题(每题3分,共计30分)
-
1. 下列各数中,是有理数的是( ).A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、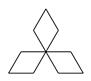 C、
C、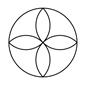 D、
D、 4. 如图是几个小正方体组成的一个几何体,这个几何体的俯视图是( )
4. 如图是几个小正方体组成的一个几何体,这个几何体的俯视图是( )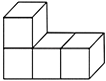 A、
A、 B、
B、 C、
C、 D、
D、 5. 在一个不透明的盒子中,装有质地、大小一样的白色乒乓球2个,黄色乒乓球3个,随机摸出一个球,摸到黄色乒乓球的概率是( )A、 B、 C、 D、6. 数据显示快递业务逐年增加,2021年至2023年快递业务收入由5000亿元增加到7500亿元,设2021年至2023年快递业务收入的年平均增长率为 , 则可列方程为( ).A、 B、 C、 D、7. 如图,AB为的直径,CD是的切线,切点为 , 连接AC,若 , 则的度数为( ).
5. 在一个不透明的盒子中,装有质地、大小一样的白色乒乓球2个,黄色乒乓球3个,随机摸出一个球,摸到黄色乒乓球的概率是( )A、 B、 C、 D、6. 数据显示快递业务逐年增加,2021年至2023年快递业务收入由5000亿元增加到7500亿元,设2021年至2023年快递业务收入的年平均增长率为 , 则可列方程为( ).A、 B、 C、 D、7. 如图,AB为的直径,CD是的切线,切点为 , 连接AC,若 , 则的度数为( ). A、30° B、40° C、50° D、60°8. 已知点 , 在反比例函数的图象上,当时,有 , 则的取值范围是( ).A、 B、 C、 D、9. 如图,点是□ABCD的边BA延长线上一点,连接CE,交边AD于点F,则下列各式正确的是( )
A、30° B、40° C、50° D、60°8. 已知点 , 在反比例函数的图象上,当时,有 , 则的取值范围是( ).A、 B、 C、 D、9. 如图,点是□ABCD的边BA延长线上一点,连接CE,交边AD于点F,则下列各式正确的是( ) A、 B、 C、 D、10. 春节假期,小星一家从家出发驾车前往某景点旅游,在行驶过程中,汽车离景点的路程y(km)与所有时间x(h)之间的函数关系的图象如图所示,下列说法正确的是( )
A、 B、 C、 D、10. 春节假期,小星一家从家出发驾车前往某景点旅游,在行驶过程中,汽车离景点的路程y(km)与所有时间x(h)之间的函数关系的图象如图所示,下列说法正确的是( ) A、小星家离景点的路程为50km B、小星从家出发第1小时的平均速度为75km/h C、小星从家出发2小时离景点的路程为125km D、小星从家到景点的时间共用了3h
A、小星家离景点的路程为50km B、小星从家出发第1小时的平均速度为75km/h C、小星从家出发2小时离景点的路程为125km D、小星从家到景点的时间共用了3h二、填空题(每题3分,共计30分)
-
11. 在百度中搜索“龘龘”,能搜到与之相关的结果个数约为226000,这个数用科学记数法表示为 .12. 函数 的自变量x的取值范围是13. 计算的结果是 .14. 分解因式 .15. 抛物线与轴的交点坐标是 .16. 不等式组 的解集是: .17. 一个扇形的圆心角是 , 弧长是 , 则扇形的半径是cm.18. 观察如图所示的三角形数阵,则第7行的最后一个数是 .
 19. 点O是正方形ABCD的对角线AC、BD交点, , 点在BC边上,连接OF, , 则BF的长为 .20. 已知等腰直角 , , , , 延长EF交BA延长线于点 , 若 , , , 则GB的长为 .
19. 点O是正方形ABCD的对角线AC、BD交点, , 点在BC边上,连接OF, , 则BF的长为 .20. 已知等腰直角 , , , , 延长EF交BA延长线于点 , 若 , , , 则GB的长为 .
三、解答题(21、22题每题7分,23、24题每题8分,25、26、27题每题10分,共计60分)
-
21. 先化简,再求代数式值,其中 .22. 如图,在由边长为1的小正方形构成的网格中,每个小正方形的顶点叫做格点,的三个顶点均在格点上,点为AB中点,请按要求完成作图:
 (1)、作线段EF,使得 , 且 , 点在格点上;(2)、作线段EG,使得EG平分线段BC,点在格点上;(3)、连接线段FG,直接写出线段FG的长.23. 为了解春节期间游客对我市冰雪旅游服务满意度,从中随机抽取部分游客进行调查,调查结果为:A.非常满意;B.满意;C.基本满意:D.不满意四个等级.请根据如图所示的两幅不完整的统计图中信息,回答下列问题:
(1)、作线段EF,使得 , 且 , 点在格点上;(2)、作线段EG,使得EG平分线段BC,点在格点上;(3)、连接线段FG,直接写出线段FG的长.23. 为了解春节期间游客对我市冰雪旅游服务满意度,从中随机抽取部分游客进行调查,调查结果为:A.非常满意;B.满意;C.基本满意:D.不满意四个等级.请根据如图所示的两幅不完整的统计图中信息,回答下列问题: (1)、抽样调查共抽取游客多少人?(2)、请通过计算补全条形统计图,并直接写出A等级所在扇形统计图的圆心角度数;(3)、春节期间累计接待游客120万人次,请你估计对服务表示不满意的游客有多少万人次?24. 如图,在中, , 是BC的中点,是AD的中点,过点作交CE的延长线于点 , 连接BF.
(1)、抽样调查共抽取游客多少人?(2)、请通过计算补全条形统计图,并直接写出A等级所在扇形统计图的圆心角度数;(3)、春节期间累计接待游客120万人次,请你估计对服务表示不满意的游客有多少万人次?24. 如图,在中, , 是BC的中点,是AD的中点,过点作交CE的延长线于点 , 连接BF. (1)、求证:四边形ADBF是菱形;(2)、若四边形ADBF面积为S,请直接写出图中,面积为的所有三角形.25. 某水果商从批发市场用16000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.(1)、大樱桃和小樱桃的进价分别是每千克多少元?(2)、在运输过程中大樱桃损耗了 , 若大樱桃售价为每千克80元,要使此次销售获利不少于6700元,则小樱桃的售价最少应为每千克多少元?26. 如图1,是的内接三角形,点在上,是弧BD的中点,点在BC上,连接BD、AE,BD与AE于点 , .
(1)、求证:四边形ADBF是菱形;(2)、若四边形ADBF面积为S,请直接写出图中,面积为的所有三角形.25. 某水果商从批发市场用16000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.(1)、大樱桃和小樱桃的进价分别是每千克多少元?(2)、在运输过程中大樱桃损耗了 , 若大樱桃售价为每千克80元,要使此次销售获利不少于6700元,则小樱桃的售价最少应为每千克多少元?26. 如图1,是的内接三角形,点在上,是弧BD的中点,点在BC上,连接BD、AE,BD与AE于点 , . (1)、求证:;(2)、如图2,延长AE交于点 , 连接AO,交BD于点 , 求证:;(3)、如图3,在(2)的条件下,作直径BM交AG于点 , 连接AM交BD于点 , 当AC是的直径时, , , 求弦BC的长.27. 如图1,抛物线与轴交于A、B两点,与轴交于点 , 点的坐标是 , 点的坐标是 .
(1)、求证:;(2)、如图2,延长AE交于点 , 连接AO,交BD于点 , 求证:;(3)、如图3,在(2)的条件下,作直径BM交AG于点 , 连接AM交BD于点 , 当AC是的直径时, , , 求弦BC的长.27. 如图1,抛物线与轴交于A、B两点,与轴交于点 , 点的坐标是 , 点的坐标是 .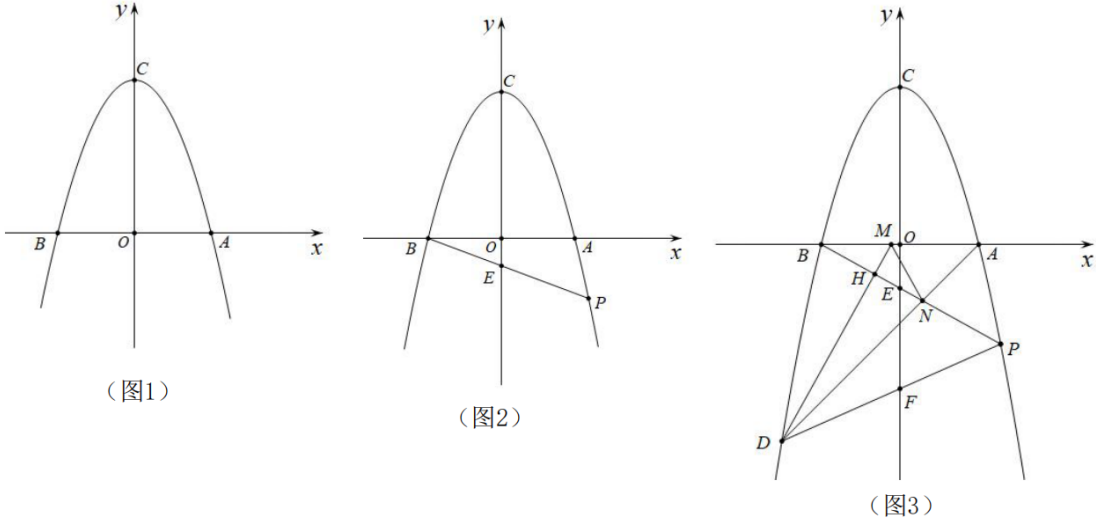 (1)、求抛物线的解析式;(2)、如图2,点是第四象限内抛物线上一点,连接PB交轴于点 , 设点的横坐标为 , 线段CE的长为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,点是第三象限内抛物线上一点,连接PD交轴于点 , 过点作于点 , 交轴于点 , 连接AD交BP于点 , 连接MN,若 , 时,求点的坐标.
(1)、求抛物线的解析式;(2)、如图2,点是第四象限内抛物线上一点,连接PB交轴于点 , 设点的横坐标为 , 线段CE的长为 , 求与之间的函数关系式,并直接写出自变量的取值范围;(3)、如图3,点是第三象限内抛物线上一点,连接PD交轴于点 , 过点作于点 , 交轴于点 , 连接AD交BP于点 , 连接MN,若 , 时,求点的坐标.