陕西省榆林市重点中学2023-2024学年九年级下学期开学考试数学试题

试卷更新日期：2024-03-11 类型：开学考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分，每小题只有一个选项是符合题意的）

1. 计算 $4 c o s 60 °$ 的值为（）

A、2 B、1 C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析
2. 下列四个几何体中，左视图是矩形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，已知AD∥BE∥CF，若AB=2BC，DF=12，则EF的长为（）

A、2 B、4 C、6 D、8

查看试题解析
4. 一个盒子中装有a个白球和4个红球（除颜色外完全相同），若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在80%，估计a的值为（）

A、40 B、30 C、16 D、50

查看试题解析
5. 在平面直角坐标系中，将抛物线 $y = x^{2} - 2 x - 3$ 向左平移2个单位，再向上平移3个单位，得到的抛物线的顶点坐标是（）

A、 $(- 1 ， - 1)$ B、 $(3 ， - 1)$ C、 $(- 3 ， - 1)$ D、 $(- 1 ， - 7)$

查看试题解析
6. 如图， $△ A B C$ 是周长为36的等腰三角形， $A B = A C$ ， $B C = 10$ ，则 $t a n B$ 的值为（）

A、 $\frac{5}{12}$ B、 $\frac{5}{13}$ C、 $\frac{12}{5}$ D、 $\frac{12}{13}$

查看试题解析
7. 如图， $A B$ 是 $⊙ O$ 的弦， $O D ⊥ A B$ 于点 $C$ ，连接 $A O$ 并延长交 $⊙ O$ 于点 $E$ ，连接 $E C$ ．已知 $A B = 8$ ， $C D = 2$ ，则 $C E$ 的长为（）

A、8 B、 $3 \sqrt{13}$ C、 $2 \sqrt{15}$ D、 $2 \sqrt{13}$

查看试题解析
8. 当 $- 2 \leq x \leq 1$ 时，二次函数 $y = - (x - m)^{2} + 5$ 有最大值4，则实数 $m$ 的值为（）

A、－3 B、2或－3 C、－1或2 D、2或－3或－1

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

9. 若 $x = 2$ 是关于 $x$ 的一元二次方程 $x^{2} + x - 2 m = 0$ 的一个根，则 $m$ 的值为．

查看试题解析
10. 一个正多边形的边长为2，中心角为 $45 °$ ，则这个正多边形的周长是．

查看试题解析
11. 已知 $△ A B C ~ △ D E F$ ， $△ A B C$ 和 $△ D E F$ 的面积分别为9和16，若 $A B = 3$ ，则 $D E$ 的长为．

查看试题解析
12. 如图，点 $A (2 ， 4)$ 、 $B (m ， 2)$ 在反比例函数 $y = \frac{k}{x}$ （ $k$ 为常数且 $k \neq 0 ， x > 0)$ 的图象上， $A C ⊥ x$ 轴于点 $C$ ， $B D ⊥ x$ 轴于点 $D$ ，连接 $O A$ 、 $O B$ ，则 $△ A O C$ 与 $△ B O D$ 重叠部分（阴影部分）的面积为．

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点 $E$ 是 $A D$ 边上的动点，连接 $B E$ ，点 $M$ 是点 $A$ 关于直线 $B E$ 的对称点，连接 $D M$ 、 $E M$ ，则 $D M$ 的最小值是．

查看试题解析

三、解答题（共13小题，计81分．解答应写出过程）

14. 解方程： $2 x^{2} - x - 3 = 0$ .

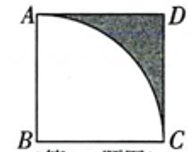
查看试题解析
15. 如图，在正方形 $A B C D$ 中， $A D = 4$ ，以点 $B$ 为圆心， $B C$ 长为半径画弧，求阴影部分的面积（结果保留 $π$ ）

查看试题解析
16. 已知反比例函数 $y = \frac{2 k - 4}{x} (k$ 为常数且 $k \neq 2$ ），若在每个象限内，函数值 $y$ 随 $x$ 的增大而减小，求 $k$ 的取值范围．

查看试题解析
17. 如图，已知点 $A$ 、 $B$ 、 $C$ 不在同一条直线上，请用尺规作图法作经过 $A$ 、 $B$ 、 $C$ 三点的 $⊙ O$ ．（不写作法，保留作图痕迹）

查看试题解析
18. 如图，在 $▱ A B C D$ 中，点E，F分别在BC，CD上，连接AE，EF，FA，若AE=AF，CE=CF．求证：四边形ABCD是菱形．

查看试题解析
19. 随着人类社会的发展，青少年应亲近大自然．某中学为了能够让学生感受大自然的美好和大千世界的美妙，于是在校内开展了以自然与社会为主题的选修课．已知有四个课题A．《草虫春秋》，B．《中华鸟兽》，C．《山河故人》，D．《文明外传》都深受学生欢迎，但需要从中选择2个课题作为本学期选修课的课程，于是将写有这四个编号的卡片（除编号和内容外，其余完全相同）背面朝上放置，洗匀放好，从中先随机抽取一张卡片不放回，再从剩下的三张卡片中随机抽取一张．

(1)、第一次抽中的卡片上的课题是B．《中华鸟兽》的概率是；

(2)、请用列表或画树状图的方法，求两次抽到的两张卡片中恰好有一张的课题是A．《草虫春秋》的概率．

查看试题解析
20. 某校组织活动，一小组需在室外搭建临时木屋，板对地面的压强p（Pa）是木板面积S（ $m^{2}$ ）的反比例函数，其图象如图所示，当木板的压强为500Pa时，求木板的面积．

查看试题解析
21. 如图，在P处有一灯塔，一艘轮船位于灯塔P的南偏东60°方向，距离灯塔45海里的A处，该轮船沿北偏东30°方向航行一段时间后，到达位于灯塔P的北偏东67°方向上的B处，求此时轮船与灯塔P的距离PB．（参考数据： $s i n 37 ° \approx \frac{3}{5}$ ， $c o s 37 ° \approx \frac{4}{5}$ ， $t a n 37 ° \approx \frac{3}{4}$ ）

查看试题解析
22. 某服装店于12月初购进了一批保暖衣．在销售中发现：该保暖衣平均每天可售出20件，每件盈利40元．为了迎接“元旦”，商场决定采取适当的降价活动，以扩大销售量，增加盈利．经市场调查发现：如果每件保暖衣每降价1元，那么平均每天就可多售出2件．要想平均每天销售这种保暖衣能盈利1200元，又能尽快减少库存，求每件保暖衣应降价多少元？

查看试题解析
23. 学习了相似三角形相关知识后，小明和同学们想利用标杆测量大楼的高度CD．如图，小明站立在地面点F处，他的同学在点B处竖立标杆AB，此时小明的头顶E、标杆顶端A、大楼顶端C在一条直线上（点F、B、D也在一条直线上）．已知小明的身高EF=1.5m，标杆AB=2.5m，BD=23m，FB=2m，EF、AB、CD均垂直于地面FD．求大楼的高度CD．

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径，点 $D$ 在直径 $A B$ 上， $C D ⊥ A B$ ， $C D = A B$ ，连接 $C B$ ，与 $⊙ O$ 相交于点 $F$ ，过点 $F$ 作 $⊙ O$ 的切线 $E F$ ，交 $C D$ 于点 $E$ ．

(1)、求证： $E F = E C$ ；

(2)、若点 $D$ 是 $O A$ 的中点， $A B = 4$ ，求 $B F$ 的长．

查看试题解析
25. 冬季来临之前，学校劳动社团的同学打算为蔬菜基地设计一款蔬菜大棚，大棚使用钢结构的骨架，上面覆上一层保温塑料膜，这样就形成了一个温室空间．如图，该大棚的横截面可以看作由矩形 $A B C D$ 和地物线 $A E D$ 构成，其中 $A B = 1 m$ ， $B C = 4 m$ ．同学们以 $B C$ 的中点 $O$ 为坐标原点， $B C$ 所在直线为 $x$ 轴， $B C$ 的中垂线 $O E$ 为 $y$ 轴建立平面直角坐标系，抛物线的顶点 $E$ 的坐标为 $(0 ， 2)$ ．

(1)、求抛物线的函数表达式；

(2)、如图，为了让大棚通风，同学们设计了两个边长为 $0.75 m$ 的正方形通风孔LFGT和 $S M N R$ ，点 $L$ 、 $R$ 均在抛物线上，点 $F$ 、 $G$ 、 $M$ 、 $N$ 在 $A D$ 所在的水平线上，求两个通风孔之间的距离 $G M$ 的长．

查看试题解析
26.

(1)、【问题提出】如图1，在四边形 $A D E C$ 中， $∠ D = ∠ E = 90 °$ ，点 $B$ 是 $D E$ 上一点，连接 $A B$ 、 $B C$ ，若 $∠ A B C = 90 °$ ，求证： $△ A D B ~ △ B E C$ ；

(2)、【问题探究】如图2，在 $R t △ A D E$ 中， $∠ D = 90 °$ ，点 $B$ 是 $D E$ 上一点，过点 $B$ 作 $B C ⊥ A B$ 交 $A E$ 于点 $C$ ，若 $t a n ∠ B A C = \frac{1}{2}$ ， $B D = 4$ ， $C E = 3$ ，求 $t a n E$ 的值；

(3)、【问题解决】如图3，四边形 $A B C D$ 是某公园的一块空地， $B C = 40 m$ ，分别沿 $A C$ 、 $B D$ 修两条小路，并在 $△ B C D$ 区域内栽种竹子，其余部分进行绿化，已知 $A B = A C$ ， $∠ A C D = 90 °$ ， $t a n ∠ C A D = \frac{1}{2}$ ，求栽种竹子的面积（即 $△ B C D$ 的面积）．

查看试题解析