吉林省四平市伊通满族自治县2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-03-11 类型:期末考试
一、单项选择题(每小题3分,共18分)
-
1. 抛物线与的共同特点是( )A、开口都向上 B、对称轴都是y轴 C、都有最高点 D、都是y随x的增大而增大2. 下列方程有两个相等的实数根的是( )A、 B、 C、 D、3. 下列说法中,正确的是( )A、不可能事件发生的概率为0 B、随机事件发生的概率为 C、概率很小的事件不可能发生 D、投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次4. 用配方法解方程时,原方程应变形为( )A、 B、 C、 D、5. 如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连接AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
 A、50° B、65° C、100° D、130°6. 如图,在中, , 将绕点A逆时针旋转,点B落在点D处,则B、D两点间的距离为( )
A、50° B、65° C、100° D、130°6. 如图,在中, , 将绕点A逆时针旋转,点B落在点D处,则B、D两点间的距离为( ) A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题(每小题4分,共32分)
-
7. 若关于x的一元二次方程有一个根为 , 则 .8. 若A(-2,a),B(1,b),C(2,c)为二次函数 的图象上的三点,则a , b , c的大小关系是 . (用“<”连接)9. 若点与关于原点中心对称,则的值为 .10. 如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE= .
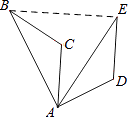 11. 二次函数y=﹣2(x﹣4)2+8的最大值为 .12. 制造一种商品,原来每件成本为100元,由于连续两次降低成本,现在的成本是每件81元,则平均每次降低成本的百分数是 .13. 如图,为的直径,点C , 点D在上,并且在直径的两侧, , 则 .
11. 二次函数y=﹣2(x﹣4)2+8的最大值为 .12. 制造一种商品,原来每件成本为100元,由于连续两次降低成本,现在的成本是每件81元,则平均每次降低成本的百分数是 .13. 如图,为的直径,点C , 点D在上,并且在直径的两侧, , 则 .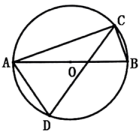 14. 如图,一枚飞镖游戏板由大小相等的小正方形格子构成向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 .
14. 如图,一枚飞镖游戏板由大小相等的小正方形格子构成向游戏板随机投掷一枚飞镖,击中黑色区域的概率是 .
三、解答题(每小题5分,共20分)
-
15. 如图,已知二次函数的图象,利用图象回答:
 (1)、一元二次方程的解是;(2)、当时,x的取值范围是;(3)、当时,y的取值范围是 .16. 解方程:17. 如图所示,在正方形网格中,每个小正方形的边长都是1个单位长度在平面直角坐标系内,三个顶点的坐标分别为 , , . 请你作出绕点O顺时针方向旋转后得到的 , 点A、B、C的对应点分别是点、、 .
(1)、一元二次方程的解是;(2)、当时,x的取值范围是;(3)、当时,y的取值范围是 .16. 解方程:17. 如图所示,在正方形网格中,每个小正方形的边长都是1个单位长度在平面直角坐标系内,三个顶点的坐标分别为 , , . 请你作出绕点O顺时针方向旋转后得到的 , 点A、B、C的对应点分别是点、、 . 18. 如图,在的正方形网格纸中,每个小正方形的边长均为1,点O , A , B为格点,即是小正方形的顶点,若将扇形围成一个圆锥,求这个圆锥的底面圆的半径的最大长度.
18. 如图,在的正方形网格纸中,每个小正方形的边长均为1,点O , A , B为格点,即是小正方形的顶点,若将扇形围成一个圆锥,求这个圆锥的底面圆的半径的最大长度.
四、解答题(每小题7分,共14分)
-
19. 人工智能是数字经济高质量发展的引擎,也是新一轮科技革命和产业变革的重要驱动.人工智能市场分为决策类人工智能,人工智能机器人,语音类人工智能,视觉类人工智能四大类型,将四个类型的图标依次制成A , B , C , D四张卡片(卡片背面完全相同),将四张卡片背面朝上洗匀放置在桌面上.
A.决策类人工智能
 B.人工智能机器人
B.人工智能机器人 C.语音类人工智能
C.语音类人工智能 D.视觉类人工智能
D.视觉类人工智能 (1)、随机抽取一张,抽到决策类人工智能的卡片的概率为;(2)、从中随机抽取一张,记录卡片的内容后放回洗匀,再随机抽取一张,请用列表或树状图的方法求抽取到的两张卡片内容一致的概率.20. 某旅游团旅游结束时,其中一位游客建议大家互相握手道别,细心的小明发现,每两位参加旅游的人互握一次手,共握了45次手,问这个旅游团共有多少位游客?
(1)、随机抽取一张,抽到决策类人工智能的卡片的概率为;(2)、从中随机抽取一张,记录卡片的内容后放回洗匀,再随机抽取一张,请用列表或树状图的方法求抽取到的两张卡片内容一致的概率.20. 某旅游团旅游结束时,其中一位游客建议大家互相握手道别,细心的小明发现,每两位参加旅游的人互握一次手,共握了45次手,问这个旅游团共有多少位游客?五、解答题(每小题8分,共16分)
-
21. 为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.(1)、求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本);(2)、当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?22. 已知:如图,在中, , D是的中点.以为直径作 , 交边于点P , 连接 , 交于点E .
 (1)、求证:是的切线;(2)、若是的切线, , 求的长.
(1)、求证:是的切线;(2)、若是的切线, , 求的长.六、解答题(每小题10分,共计20分)
-
23. 已知是等腰三角形, , 将绕点逆时针旋转得到 , 点、点的对应点分别是点、点 .
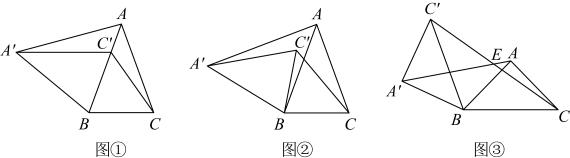 (1)、感知:如图①,当落在边上时,与之间的数量关系是:(不需要证明);(2)、探究:如图②,当落在的左侧时,与是否相等?如果相等,请证明;如果不相等,请说明理由;(3)、应用:如图③,若 , 、交于点 , 则度.24. 如图所示,在平面直角坐标系中,抛物线与x轴交于点 , 点 . 与y轴交于点C . 点P在第一象限的抛物线上,过点P作x轴的平行线分别交y轴和直线BC于点D和点E . 设点P的横坐标为m , 线段的长度为d .
(1)、感知:如图①,当落在边上时,与之间的数量关系是:(不需要证明);(2)、探究:如图②,当落在的左侧时,与是否相等?如果相等,请证明;如果不相等,请说明理由;(3)、应用:如图③,若 , 、交于点 , 则度.24. 如图所示,在平面直角坐标系中,抛物线与x轴交于点 , 点 . 与y轴交于点C . 点P在第一象限的抛物线上,过点P作x轴的平行线分别交y轴和直线BC于点D和点E . 设点P的横坐标为m , 线段的长度为d . (1)、求这条抛物线对应的函数解析式;(2)、求d关于m的函数解析式;(3)、在(2)的条件下,当时,求m的值.
(1)、求这条抛物线对应的函数解析式;(2)、求d关于m的函数解析式;(3)、在(2)的条件下,当时,求m的值.