吉林省长春市新区2023-2024学年九年级上学期期末数学试卷
试卷更新日期:2024-03-11 类型:期末考试
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 若使二次根式在实数范围内有意义,则x的取值范围是 ( )
A、x≥2 B、x>2 C、x<2 D、x≤22. 用配方法解方程 , 配方后的方程是( )A、 B、 C、 D、3. 如图,直线 , 直线、分别与直线、、相交于点、、和点、、 , 若 , , , 则( ) A、 B、 C、 D、4. 如图,在综合实践活动中,小明在学校门口的点处测得树的顶端仰角为 , 同时测得米,则树的高单位:米为( )
A、 B、 C、 D、4. 如图,在综合实践活动中,小明在学校门口的点处测得树的顶端仰角为 , 同时测得米,则树的高单位:米为( ) A、 B、 C、 D、5. 是方程的一个根,则代数式的值是( )A、 B、 C、 D、6. 已知点、、都在函数的图象上,则、、的大小关系为( )A、 B、 C、 D、7. 在△ 中, ,用直尺和圆规在AC上确定点D,使△BAD∽△CBD,根据作图痕迹判断,正确的是( )A、
A、 B、 C、 D、5. 是方程的一个根,则代数式的值是( )A、 B、 C、 D、6. 已知点、、都在函数的图象上,则、、的大小关系为( )A、 B、 C、 D、7. 在△ 中, ,用直尺和圆规在AC上确定点D,使△BAD∽△CBD,根据作图痕迹判断,正确的是( )A、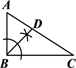 B、
B、 C、
C、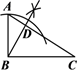 D、
D、 8. 如图,在平行四边形中,为上一点,:: , 连结 , 交于点 , 若的面积为 , 则四边形的面积等于( )
8. 如图,在平行四边形中,为上一点,:: , 连结 , 交于点 , 若的面积为 , 则四边形的面积等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共6小题,每小题3分,共18分。
-
9. 如图,与位似,点为位似中心,若:: , 则: .
 10. 如果关于的一元二次方程有两个同号实数根,则的取值范围是 .11. 将抛物线向右平移个单位所得函数解析式为 .12. 二次函数的图象如图所示,则函数值时,的取值范围是 .
10. 如果关于的一元二次方程有两个同号实数根,则的取值范围是 .11. 将抛物线向右平移个单位所得函数解析式为 .12. 二次函数的图象如图所示,则函数值时,的取值范围是 . 13. 拦水坝横断面如图所示,迎水坡的坡比是 , 坝高 , 则坡面的长度是
13. 拦水坝横断面如图所示,迎水坡的坡比是 , 坝高 , 则坡面的长度是 14. 如图,同学们在操场上玩跳大绳游戏,绳甩到最高处时的形状是抛物线型,摇绳的甲、乙两名同学拿绳的手的间距为米,到地面的距离与均为米,绳子甩到最高点处时,最高点距地面的垂直距离为米身高为米的小吉站在距点水平距离为米处,若他能够正常跳大绳绳子甩到最高时超过他的头顶 , 则的取值范围是 .
14. 如图,同学们在操场上玩跳大绳游戏,绳甩到最高处时的形状是抛物线型,摇绳的甲、乙两名同学拿绳的手的间距为米,到地面的距离与均为米,绳子甩到最高点处时,最高点距地面的垂直距离为米身高为米的小吉站在距点水平距离为米处,若他能够正常跳大绳绳子甩到最高时超过他的头顶 , 则的取值范围是 .
三、解答题:本题共10小题,共78分。解答应写出文字说明,证明过程或演算步骤。
-
15. 计算: .16. 年第届亚运会在杭州举办小蔡作为亚运会的志愿者“小青荷”为大家提供咨询服务现有如图所示“杭州亚运会吉祥物”的三盒盲盒供小蔡选择,分别记为 , , 小蔡从中随机抽取两盒请用列表或画树状图的方法,求小蔡抽到的两盒吉祥物恰好是和的概率.
 17. 每当秋冬季节交替的时间,感冒药品的销量就会大幅增长,药店利润也有所提高,某药店九月份的销售利润是元,而十一月份的销售利润为元,求该药店利润平均每月的增长率.18. 在中,是斜边上的高.
17. 每当秋冬季节交替的时间,感冒药品的销量就会大幅增长,药店利润也有所提高,某药店九月份的销售利润是元,而十一月份的销售利润为元,求该药店利润平均每月的增长率.18. 在中,是斜边上的高.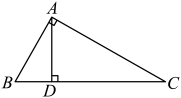 (1)、证明:;(2)、若 , 求的长.19. 图、图、图均是的正方形网格,每个小正方形的顶点称为格点,的顶点均在格点上只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)、证明:;(2)、若 , 求的长.19. 图、图、图均是的正方形网格,每个小正方形的顶点称为格点,的顶点均在格点上只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹. (1)、在图中,画出中边上的中线 .
(1)、在图中,画出中边上的中线 .
(2)、在图中,在边上找到一点 , 连结 , 使:: .
(3)、在图中,在边上找到一点 , 连结 , 使 .20. 下表是某厂质检部门对该厂生产的一批排球质量检测的情况.抽取的排球数描取格品数
合格品数
合格品频率
 (1)、求出表中 , .
(1)、求出表中 , .
(2)、从这批排球中任意抽取一个,是合格品的概率约是 精确到
(3)、如果生产个排球,那么估计该厂生产的排球合格的有多少个?21. 已知,抛物线与轴交于点 , 与轴交于 , 两点,点在点左侧.(1)、直接写出、、三点的坐标;
(2)、当时,求的最大值与最小值之差.22. 【教材呈现】如图是华师版九年级上册数学教材第页的部分内容.如图,在中,点、分别是与的中点,根据画出的图形,可以猜想: , 且 .
对此,我们可以用演绎推理给出证明无需证明
 (1)、【感知】如图 , 在中, , , 、是的中线,、分别是和的中点,求的长;
(1)、【感知】如图 , 在中, , , 、是的中线,、分别是和的中点,求的长;
(2)、【应用】如图 , 在中,、分别是、的中点,连接 , 将绕点逆时针旋转一定的角度 , 连接、 , 若 , 则 ;
(3)、【拓展】如图 , 在等边中,是射线上一动点点在点右侧 , 连接 , 把线段绕点逆时针旋转得到线段 , 连接 , 是中点,连接、 , 若 , , 则 .23. 如图,在▱中, , , 点从点出发,沿折线以每秒个单位长度的速度向终点运动点不与点、、重合在点的运动过程中,过点作所在直线的垂线,交边或边于点 , 以为一边作矩形 , 且 , 与在的同侧设点的运动时间为秒 . (1)、的值为 .
(1)、的值为 .
(2)、直接写出线段的长用含的代数式表示
(3)、当的面积等于时,求的值.
(4)、连接 , 当将矩形分成的两部分的面积比为:时,直接写出的值.24. 如图 , 在平面直角坐标系内,抛物线与轴交于、两点,与直线交于、两点,且抛物线的顶点的坐标为 .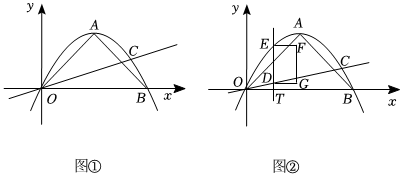 (1)、直接写出点的坐标 ;的形状为: ;
(1)、直接写出点的坐标 ;的形状为: ;
(2)、求抛物线的解析式;
(3)、如图 , 点是线段上的一个动点,过点作轴的平行线交直线于点 , 交抛物线于点 , 以为一边,在的右侧作矩形 , 且 .
当矩形的面积随着的增大而增大时,求的取值范围;
当矩形与有重叠且重叠部分为轴对称图形时,直接写出的取值范围.