北师大版数学八年级下册单元清测试(第三章)培优卷
试卷更新日期:2024-03-10 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆
 B、西藏博物馆
B、西藏博物馆 C、广东博物馆
C、广东博物馆 D、湖北博物馆
D、湖北博物馆 2. 下列图形中,能由图形通过平移得到的是( )
2. 下列图形中,能由图形通过平移得到的是( )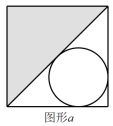 A、
A、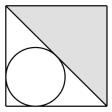 B、
B、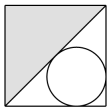 C、
C、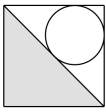 D、
D、 3. 如图,点 , 将线段先向上平移2个单位长度,再向左平移3个单位长度,得到线段 , 则点的对应点的坐标是( )
3. 如图,点 , 将线段先向上平移2个单位长度,再向左平移3个单位长度,得到线段 , 则点的对应点的坐标是( )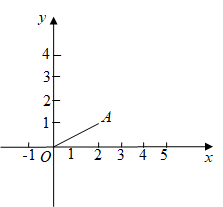 A、 B、 C、 D、4. 如图,Rt△ABC中,∠ACB = 90°,AB = 5,AC= 3,把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C' ,则四边形ABC'A'的面积是 ( )
A、 B、 C、 D、4. 如图,Rt△ABC中,∠ACB = 90°,AB = 5,AC= 3,把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C' ,则四边形ABC'A'的面积是 ( )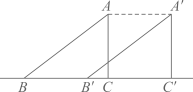 A、15 B、18 C、20 D、225. 将直线 向上平移两个单位,平移后的直线所对应的函数关系式为( )A、 B、 C、 D、6. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )
A、15 B、18 C、20 D、225. 将直线 向上平移两个单位,平移后的直线所对应的函数关系式为( )A、 B、 C、 D、6. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )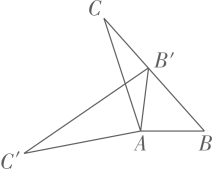 A、 B、 C、 D、7. 已知点是等边的边上的一点,若 , 则在以线段为边的三角形中,最小内角的大小为( )A、 B、 C、 D、8. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )
A、 B、 C、 D、7. 已知点是等边的边上的一点,若 , 则在以线段为边的三角形中,最小内角的大小为( )A、 B、 C、 D、8. 如图,中, , 将绕点顺时针旋转得到 , 使点的对应点恰好落在边上,、交于点 . 若 , 则的度数是(用含的代数式表示)( )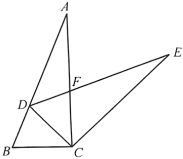 A、 B、 C、 D、9. 如图,在平面内将五角星绕其中心旋转180°后所得到的图案是( )
A、 B、 C、 D、9. 如图,在平面内将五角星绕其中心旋转180°后所得到的图案是( ) A、
A、 B、
B、 C、
C、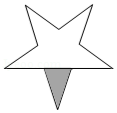 D、
D、 10. 如图,△AOB中,OA=4,OB=6,AB=2 ,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )
10. 如图,△AOB中,OA=4,OB=6,AB=2 ,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )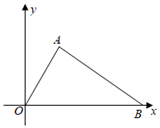 A、(4,2)或(﹣4,2) B、(2 ,﹣4)或(﹣2 ,4) C、(﹣2 ,2)或(2 ,﹣2) D、(2,﹣2 )或(﹣2,2 )
A、(4,2)或(﹣4,2) B、(2 ,﹣4)或(﹣2 ,4) C、(﹣2 ,2)或(2 ,﹣2) D、(2,﹣2 )或(﹣2,2 )二、填空题(每题3分,共18分)
-
11. 如图,在平面直角坐标系中,的三个顶点坐标分别为 . 若将向左平移3个单位长度得到 , 则点A的对应点的坐标是 .
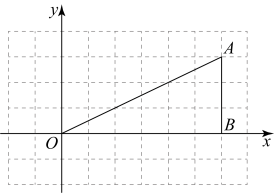 12. 如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(-3,4)的对应点是A1(2,5),则点B(-4,2)的对应点B1的坐标是 .
12. 如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(-3,4)的对应点是A1(2,5),则点B(-4,2)的对应点B1的坐标是 . 13. 如图,将绕点A逆时针旋转角得到 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数是.
13. 如图,将绕点A逆时针旋转角得到 , 点B的对应点D恰好落在边上,若 , 则旋转角的度数是.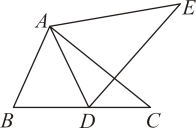 14. 如图,在 中, , .将 绕点B逆时针旋转60°,得到 ,则 边的中点D与其对应点 的距离是.
14. 如图,在 中, , .将 绕点B逆时针旋转60°,得到 ,则 边的中点D与其对应点 的距离是.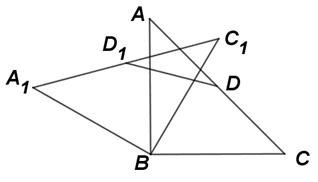 15. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 .
15. 如图,直线 , 的边在直线上, , 将绕点顺时针旋转至 , 边交直线于点 , 则 . 16. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .
16. 如图,在△ABC中,∠C=90°,∠B=30°,AB=6,将△ABC绕点A逆时针方向旋转15°得到△AB′C′,B′C′交AB于点E,则B′E= .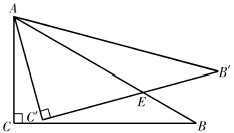
三、解答题(共7题,共72分)
-
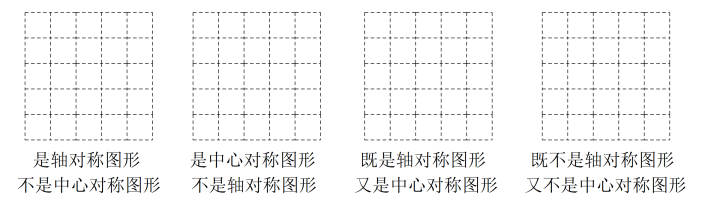
17. 将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
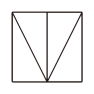
 18. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
18. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.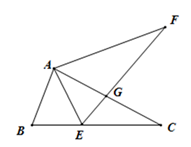 (1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.19. 如图,在5×5的方格纸中,线段AB的端点均在格点上,请按要求画图.
(1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.19. 如图,在5×5的方格纸中,线段AB的端点均在格点上,请按要求画图. (1)、如图1,画出一条线段AC , 使AC=AB , C在格点上;(2)、如图2,画出一条线段EF , 使EF , AB互相平分,E , F均在格点上;(3)、如图3,以A , B为顶点画出一个四边形,使其是中心对称图形,且顶点均在格点上.20. 如图,在平面直角坐标系xOy中,A(-1,2).
(1)、如图1,画出一条线段AC , 使AC=AB , C在格点上;(2)、如图2,画出一条线段EF , 使EF , AB互相平分,E , F均在格点上;(3)、如图3,以A , B为顶点画出一个四边形,使其是中心对称图形,且顶点均在格点上.20. 如图,在平面直角坐标系xOy中,A(-1,2). (1)、将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是.(2)、点C与点A关于原点O对称,则点C的坐标是.(3)、反比例函数的图象经过点B,则它的解析式是.(4)、一次函数的图象经过A,C两点,则它的解析式是.21.
(1)、将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是.(2)、点C与点A关于原点O对称,则点C的坐标是.(3)、反比例函数的图象经过点B,则它的解析式是.(4)、一次函数的图象经过A,C两点,则它的解析式是.21.已知:正方形ABCD.
(1)如图1,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系和位置关系分别是什么?请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当a=90°时,连接BE、DF,猜想沟AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.
 22. 下面是小明关于“对称与旋转的关系”的探究过程,请你补充完整.
22. 下面是小明关于“对称与旋转的关系”的探究过程,请你补充完整.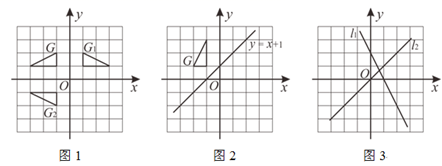 (1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .23. 已知 和 都是等腰直角三角形 , .
(1)、三角形在平面直角坐标系中的位置如图1所示,简称G , G关于y轴的对称图形为 ,关于 轴的对称图形为 .则将图形 绕点顺时针旋转度,可以得到图形 .(2)、在图2中分别画出G关于y轴和直线 的对称图形 , . 将图形 绕 点(用坐标表示)顺时针旋转 度,可以得到图形 .(3)、综上,如图3,直线 和 所夹锐角为 ,如果图形G关于直线 的对称图形为 ,关于直线 的对称图形为 ,那么将图形 绕点(用坐标表示)顺时针旋转度(用 表示),可以得到图形 .23. 已知 和 都是等腰直角三角形 , .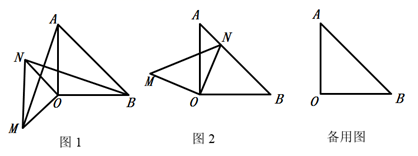 (1)、如图1:连 ,求证: ;(2)、若将 绕点O顺时针旋转,
(1)、如图1:连 ,求证: ;(2)、若将 绕点O顺时针旋转,①如图2,当点N恰好在 边上时,求证: ;
②当点 在同一条直线上时,若 ,请直接写出线段 的长.