【培优卷】2024年浙教版数学七年级下册3.3多项式的乘法同步练习

试卷更新日期：2024-03-10 类型：同步测试

进入出卷网下载

一、选择题

1. 若关于 $x$ 的代数式 $(x^{2} + m x) (x - 3)$ 化简后不含有 $x^{2}$ 项，则 $m$ 的值为（）

A、 $- 3$ B、1 C、3 D、4

查看试题解析
2. 若 $(x + m) (x^{2} + n x + 1)$ 的展开式中常数项为-2，且不含 $x^{2}$ 项，则展开式中一次项的系数为（）

A、-2 B、2 C、3 D、-3

查看试题解析
3. 若 $(x^{2} - 2 x + 3) (x^{2} + m x + n)$ 的展开式中不含 $x^{3}$ 项和x项，则m，n的值应该是（）

A、 $m = 2 ， n = 3$ B、 $m = 2 ， n = - 3$ C、 $m = - 2 ， n = 3$ D、 $m = - 2 ， n = - 3$

查看试题解析
4. 长方形一边长为 $2 a + b ，$ 另一边比它小 $a - b$ 则长方形面积为（）

A、 $2 a^{2} + a b - b^{2}$ B、 $2 a^{2} + a b$ C、 $4 a^{2} + 4 a b + b^{2}$ D、 $2 a^{2} + 5 a b + 2 b^{2}$

查看试题解析
5. 将多项式 $[(17 x^{2} - 3 x + 4) - (a x^{2} + b x + c)]$ 除以 $5 x + 6$ 后得商式 $2 x + 1$ ，余式为0，则 $a - b - c$ 的值为（）

A、3 B、23 C、25 D、29

查看试题解析
6. 聪聪计算一道整式乘法的题：（x+m）（5x-4），由于聪聪将第一个多项式中的“+m”抄成“-m”，得到的结果为5x²-34x+24．这道题的正确结果是（）

A、5x²+26x-24 B、5x²-26x-24 C、5x²+34x-24 D、5x²-34x-24

查看试题解析
7. 如图所示，在长方形 $A B C D$ 中，横向涂色部分是长方形，另一涂色部分是平行四边形，则空白部分的面积是（）

A、 $b c - a b + a c + c^{2}$ B、 $a b - b c - a c + c^{2}$ C、 $a^{2} + a b + b c - a c$ D、 $b^{2} - b c + a^{2} - a b$

查看试题解析
8. 综合与实践课上，小颖将长方形硬纸片的四个角处剪去边长为x的小正方形，再按折痕(虚线)折叠，可以制成有底无盖的长方体盒子，根据图中信息，该长方体盒子的体积可表示为(　　)

A、 $4 x^{3} + 16 x^{2} - 15 x$ B、 $4 x^{3} - 4 x^{2} + 15 x$ C、 $4 x^{3} + 4 x^{2} + 15 x$ D、 $4 x^{3} - 16 x^{2} + 15 x$

查看试题解析

二、填空题

9. 阅读以下问题的解答过程：若多项式 $2 x^{2} - x + a$ 能被 $x - 2$ 整除，求常数a的值．解法如下：
∵二次三项式 $2 x^{2} - x + a$ 中最高次项是 $2 x^{2}$ ，已知因式 $(x - 2)$ 中最高次项是x ，

又∵ $x \cdot 2 x = 2 x^{2}$ ，

∴另一因式的最高次项应为 $2 x$ ．因此，可设另一因式为 $(2 x + m)$ （其中m是常数项）．

即得， $2 x^{2} - x + a = (x - 2) (2 x + m)$ ． ∴ $2 x^{2} - x + a = 2 x^{2} + (m - 4) x - 2 m$ ．

可得 $- 1 = m - 4$ ， $a = - 2 m$ ． ∴ $m = 3$ ， $a = - 6$ ．

仿照以上解题方法，解答以下问题：已知 $3 x^{3} + k x^{2} + 1$ 被 $3 x - 1$ 整除，则k的值为．

查看试题解析
10. 符号 $|\begin{matrix} a & b \\ c & d \end{matrix}|$ 叫做二阶行列式，规定它的运算法则为 $|\begin{matrix} a & b \\ c & d \end{matrix}|$ =ad﹣bc，例如 $|\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}|$ =1×4﹣2×3=﹣2．那么，根据阅读材料，化简 $|\begin{matrix} a + 2 & a + 3 \\ a - 2 & a + 3 \end{matrix}|$ = ．

查看试题解析
11. 数学兴趣小组发现：
$(x - 1) (x + 1) = x^{2} - 1$
$(x - 1) (x^{2} + x + 1) = x^{3} - 1$
$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$
利用你发现的规律：求： $6^{2023} + 6^{2022} + 6^{2021} + \dots + 6 + 1 =$ ．

查看试题解析
12. 如图，在长方形 $A B C D$ 中， $A B = 30$ ， $B C = 20$ ，点 $E$ ， $F$ 是 $B C$ 、 $C D$ 上的点，且 $B E = D F = x$ ，分别以 $F C$ 、 $C E$ 为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C E M N$ ，若长方形 $C E P F$ 的面积为 $220$ 平方单位，则图中阴影部分的面积和为平方单位．

查看试题解析

三、解答题

13. 如图，在一块长为a米，宽为b米的长方形草地上，有一条横向的弯曲小路（小路任何地方的垂直宽度都是1个单位长度），有一条纵向的弯曲小路（小路任何地方的水平宽度都是2个单位长度）.

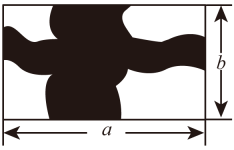(1)、请你用含a、b的式子表示绿地面积：

(2)、当 $a = 30$ 米， $b = 26$ 米时，绿地面积是多少平方米？

查看试题解析
14. 下面的式子均是多项式乘以多项式，其中第1个多项式都是 $(a - b)$ ：
第1个等式： $(a - b) (a + b) = a^{2} - b^{2}$ ；

第2个等式： $(a - b) (a^{2} + a b + b^{2}) = a^{3} - b^{3}$ ；

第3个等式： $(a - b) (a^{3} + a^{2} b + a b^{2} + b^{3}) = a^{4} - b^{4}$ ；

……

(1)、请根据规律，写出第4个等式：；

(2)、猜想： $(a - b) (a^{n - 1} + a^{n - 2} b + a^{n - 3} b^{2} + \cdot \cdot \cdot a^{2} b^{n - 3} + a b^{n - 2} + b^{n - 1}) =$ （其中 $n$ 为正整数，且 $n \geq 2$ ）；

(3)、利用（2）猜想的结论计算： $3^{9} - 3^{8} + 3^{7} - 3^{6} + \cdot \cdot \cdot + 3^{3} - 3^{2} + 3$ ．

查看试题解析
15. 阅读材料：
类比是常用的数学思想.比如，我们可以类比多位数的竖式运算方法，得到多项式与多项式的运算方法.
① $\frac{1}{2 x + 3} \frac{+ ） 3 x - 5}{5 x - 2}$
∴（2x+3）+（3x-5）=5x-2. $② 3 x^{2} - 4 x + 1$
$\frac{- ） x^{2} + 0 - 5}{2 x^{2} - 4 x + 6}$
$∴ (3 x^{2} - 4 x + 1) - (x^{2} - 5) = 2 x^{2} - 4 x + 6 ，$ ③x+3
$\frac{\times ） 2 x + 5}{5 x + 15}$
$\frac{2 x^{2} + 6 x}{2 x^{2} + 11 x + 15}$
$∴ (x + 3) (2 x + 5) = 2 x^{2} + 11 x + 15 .$
理解应用：

(1)、请仿照上面的竖式方法计算：（2x+3）（x-5）.

(2)、已知两个多项式的和为 $3 x^{2} - \frac{7}{2} x + 5 ，$ 其中一个多项式为x²-2，请用竖式的方法求出另一个多项式.

(3)、已知一个长为（x+2）、宽为（x-2）的长方形A，将它的长增加8，宽增加a得到一个新长方形B（如图），若长方形B的周长是A 的周长的3倍，求长方形 B的面积（用含x的代数式表示）.

查看试题解析

【培优卷】2024年浙教版数学七年级下册3.3多项式的乘法 同步练习

一、选择题

二、填空题

三、解答题

【培优卷】2024年浙教版数学七年级下册3.3多项式的乘法同步练习