备考2024年中考数学探究性训练专题7 二次根式
试卷更新日期:2024-03-10 类型:二轮复习
一、选择题
-
1. 某校研究性学习小组在学习二次根式 =|a|之后,研究了如下四个问题,其中错误的是( )A、在a>1的条件下化简代数式a+ 的结果为2a﹣1 B、当a+ 的值恒为定值时,字母a的取值范围是a≤1 C、a+ 的值随a变化而变化,当a取某个数值时,上述代数式的值可以为 D、若 =( )2 , 则字母a必须满足a≥12. 观察式子: , ; , ; , . 由此猜想 . 上述探究过程蕴含的思想方法是( )A、特殊与一般 B、整体 C、转化 D、分类讨论3. 已知三角形的三边长分别为a,b,c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式 , 其中;我国南宋时期数学家秦九韶(约1202—1261)曾提出利用三角形的三边求其面积的秦九韶公式 , 若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、
二、填空题
-
4. 为了简洁、明确的表示一个正数的算术平方根,许多数学家进行了探索,期间经历了400余年,直至1637年法国数学家笛卡儿在他的《几何学》中开始使用“ ”表示算数平方根.我国使用根号是由李善兰(1811-1882年)译西方数学书时引用的,她在《代数备旨》中把图1所示题目翻译为: 则图2所示题目(字母代表正数)翻译为 , 计算结果为.
 5. 斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花,飞燕草,万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用 [( )n﹣( )n]表示.
5. 斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花,飞燕草,万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用 [( )n﹣( )n]表示.通过计算求出斐波那契数列中的第1个数为 , 第2个数为 .

三、综合题
-
6. 探究:(1)、计算下列各式,并判断结果大小;
① , , 则;
② , , 则;
③ , , 则 .
(2)、根据你发现的规律,再写出一个类似的式子;(3)、用字母表示这一规律,并给出证明.7. 问题探究:因为 , 所以因为 , 所以因为 , 所以请你根据以上规律,结合你的经验化简下列各式:
(1)、;(2)、8. 在数学小组探究学习中,张兵与他的小组成员遇到这样一道题:已知 , 求的值.他们是这样解答的:
∵
∴
∴即
∴
∴ .
请你根据张兵小组的解题方法和过程,解决以下问题:
(1)、 .(2)、化简;9. 小丽根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是小丽的探究过程,请补充完整:
(1)、具体运算,发现规律,特例:
特例:
特例:
特例:填写一个符合上述运算特征的例子;
(2)、观察、归纳,得出猜想.如果为正整数,用含的式子表示上述的运算规律为:;
(3)、证明你的猜想;(4)、应用运算规律化简:.10. 探究过程:观察下列各式及其验证过程.
① ②验证:
验证:
(1)、按照上面两个等式及其验证过程的基本思路,猜想:= ; ;
(2)、通过上述探究你能猜测出: =(n>0),并验证你的结论.11. 探索规律:先观察下列等式,再回答问题:
(1)、根据上面三个等式提供的信息,请你猜想(2)、请按照上面各等式反映的规律,试写出第 n 个等式:(3)、计 算:12. 阅读理解下面内容,并解决问题:善于思考的小明在学习《实数》一章后,自己探究出了下面的两个结论:
① , , 和 都是9×4的算术平方根,
而9×4的算术平方根只有一个,所以 = .
② , , 和 都是9×16的算术平方根,
而9×16的算术平方根只有一个,所以 .
请解决以下问题:
(1)、请仿照①帮助小明完成②的填空,并猜想:一般地,当a≥0,b≥0时, 与 、 之间的大小关系是怎样的?(2)、再举一个例子,检验你猜想的结果是否符合题意.(3)、运用以上结论,计算: 的值.13. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 . 善于思考的小明进行了以下探索:
设(其中a、b、m、n均为整数),则有 .
, . 这样小明就找到了一种把类似的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)、当a、b、m、n均为正整数时,若 , 用含m、n的式子分别表示a、b,得: , ;(2)、利用所探索的结论,找一组正整数a、b、m、n填空:+=(+;(3)、若 , 且a、m、n均为正整数,求a的值?(4)、化简: .14. 阅读材料:小敏在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方.例如:3+2=(1+)2 , 善于思考的小敏进行了以下探索:
当a、b、m、n均为整数时,若a+b=(m+n)2 , 则有a+b=m2+2n2+2mn .
a=m2+2n2 , b=2mn.这样小敏就找到了一种把类似a+b的式子化为平方式的方法.
请你仿照小敏的方法探索并解决下列问题:
(1)、当a、b、m、n均为整数时,若 , 用含mn的式子分别表示a、b,则:a= , b= ;(2)、若a+6=(m+n)2 , 且a、m、n均为正整数,求a的值;(3)、直接写出式子化简的结果.15. 著名数学教育家G·波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学会数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先阅读下列材料,再解决问题:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性质化去里面的一层根号.例如: .
解决问题:
(1)、在括号内填上适当的数:①: , ②: , ③ .
(2)、根据上述思路,求出的值.16. 小明在学习了“二次根式”后,发现一些含根号的代数式可以写成另一个根号的代数式的平方,如 .善于思考的小明进行了以下探索:
设 (其中a、b、m、n均为整数),则有 . , .这样小明就找到了一种把类似 的代数式化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)、当a、b、m、n均为整数时,若 ,用含m、n的代数式分别表示a、b,则: , ;(2)、利用所探索的结论,找一组正整数a、b、m、n填空: .(3)、若 ,且a、m、n均为正整数,求a的值.17. 【知识再现】乘积为1的两个数互为倒数.如: , 我们就说2和互为倒数.【主题探究】在学习二次根式的过程中,某数学兴趣小组发现有一些特殊无理数之间也具有互为倒数的关系.例如: , 可得与互为倒数.
即 , .
类似的, , , , .
【启发应用】请根据以上规律,解决下列问题:
(1)、 , ;(为正整数)(2)、若 , 则=;(3)、计算: .18. 阅读材料:材料一:两个含有二次根式而非零的代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式.
例如: , , 我们称的一个有理化因式是 , 的一个有理化因式是 .
材料二:如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.
例如: ,
.
请你仿照材料中的方法探索并解决下列问题:
(1)、的有理化因式为 , 的有理化因式为;(均写出一个即可)(2)、将下列各式分母有理化(要求写出变形过程):①;
②;
(3)、计算:的结果.19. 若 是一个正整数,那么正整数m的最小值是多少?请探究.20. 小丽根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是小丽的探究过程,请补充完整:
(1)、具体运算,发现规律,特例1:
特:2:
特:3:
特例4: . (填写一个符合上述运算特征的例子);
(2)、观察、归纳,得出猜想.如果n为正整数,用含n的式子表示上述的运算规律为:;
(3)、证明你的猜想;(4)、应用运算规律化简:= .21. 在数学小组探究学习中,小华与他的小组成员遇到这样一道题:已知 , 求的值.他们是这样解答的:即
请你根据小华小组的解题方法和过程,解决以下问题:
(1)、.(2)、化简.(3)、若 , 求的值.22. 阅读理解:学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如.继续进行以下的探索:设(其中 , , , 都是正整数),则有.∴ , , 这样就得出了把类似的式子化为平方式的方法.请仿照上述方法探索并解决下列问题:
(1)、当 , , , 都是正整数时,若 , 用含 , 的式子分别表示 , , 得 , ;(2)、利用上述方法,填空:(-);(3)、如果 , 且 , , 都是正整数,求的值.23. 【阅读材料】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 . 善于思考的小明进行了以下探索:若设(其中均为整数),则有 . 这样小明就找到了一种把类似的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:【问题解决】
(1)、若 , 当均为整数时,则a= , b= . (均用含m、n的式子表示)(2)、若 , 且均为正整数,分别求出的值.(3)、【拓展延伸】化简= .
24. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 , 善于思考的小明进行了以下探索:设(其中a、b、m、n均为正整数),则有 ,
∴a=m2+2n2 , b=2mn.
这样小明就找到了一种把部分的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)、当a、b、m、n均为正整数时,若 , 用含m、n的式子分别表示a、b,得:a= , b=;(2)、若 , 且a、m、n均为正整数,求a的值;(3)、化简: .25. 先阅读下列解答过程,然后再解答:小芳同学在研究化简中发现:首先把化为﹐由于 , , 即: , , 所以 ,问题:
(1)、填空: , ﹔(2)、进一步研究发现:形如的化简,只要我们找到两个正数a , b(),使 , , 即 , ﹐那么便有: .(3)、化简:(请写出化简过程)26. 探究逼近 的有理近似值.方法介绍:
经过 步操作( 为正整数)不断寻找有理数 , ,使得 ,并且让 的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小 对应的点 所在线段的长度(二分法)
思路分析:
在数轴上记 , 对应的点分别为 , 和 的平均数 对应线段 的中点(记为 ).通过判断 还是 ,得到点 是在二等分后的“左线段 ”上还是“右线段 ”上,重复上述步骤,不断得到 ,从而得到 更精确的近似值.
具体操作步骤及填写“阅读活动任务单”:
(1)、当 时,①寻找左右界值:先寻找两个连续正整数 ,使得 .
因为 ,所以 ,那么 , ,线段 的中点 对应的数 .
的值
还是
点 在“左线段 ”上还是“右线段 ”上
得出更精确的 与 , , 的大小关系
1
2
3
2.5
点 在线段 上
2
2.5
3
2.75
点 在线段 上
3
2.5
2.75
2.625
4
②二分定位:判断点 在“左线段 ”上还是在“右线段 ”上.
比较7与 的大小,从而确定 与 的大小;
因为 > (填 “>”或“<”),得到点 在线段 上(填“ ”或“ ”).
(2)、当 时,在(1)中所得 的基础上,仿照以上步骤,继续进行下去,得到表中 时的相应内容.请继续仿照以上步骤操作下去,补全“阅读活动任务单”:
27. 有这样一个问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:(1)、函数的自变量x的取值范围是 ;(2)、如表是y与x的几组对应值.m的值为 ;x
1
2
3
4
…
y
0
m
1
…
(3)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;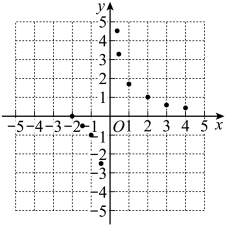 (4)、结合函数的图象,写出该函数的一条性质: .(5)、结合函数图象估计的解的个数为 个.
(4)、结合函数的图象,写出该函数的一条性质: .(5)、结合函数图象估计的解的个数为 个.