备考2024年中考数学探究性训练专题5 因式分解-在线组卷题库

1. 小明、小花和老师一起探究一个问题：将

m^{4} + 4

因式分解．

小花根据大家的提示，整理出解答过程：

$m^{2} + 4$

$= {(m^{2})}^{2} + 2^{2}$

$= {(m^{2})}^{2} + 4 m^{2} + 2^{2} - 4 m^{2}$

$= {(m^{2} + 2)}^{2} - {(2 m)}^{2}$

$= (m^{2} + 2 + 2 m) (m^{2} + 2 - 2 m)$

请你依照上述做法，将下列各式因式分解：

(1)、

4 x^{4} + 1

；

(2)、

a^{4} + c^{4} - 7 a^{2} c^{2}

查看试题解析

2. 观察“探究性学习”小组甲、乙两名同学进行的因式分解：

甲： $x^{2} - x y + 4 x - 4 y$

$= (x^{2} - x y) + (4 x - 4 y)$ （分成两组）

$= x (x - y) + 4 (x - y)$ （直接提公因式）

$= (x - y) (x + 4)$ .

乙： $a^{2} - b^{2} - c^{2} + 2 b c$

$= a^{2} - (b^{2} + c^{2} - 2 b c)$ （分成两组）

$= a^{2} - {(b - c)}^{2}$ （直接运用公式）

$= (a + b - c) (a - b + c)$ （再用平方差公式）

请你在他们解法的启发下，把下列各式分解因式：

(1)、

m^{3} - 2 m^{2} - 4 m + 8

(2)、

x^{2} - 2 x y + y^{2} - 9

.

查看试题解析

3. 阅读材料：若m²－2mn＋2n²－8n＋16＝0，求m、n的值．

解：∵m²－2mn＋2n²－8n＋16＝0，

∴（m²－2mn＋n²）＋（n²－8n＋16）＝0，

∴（m－n）²＋（n－4）²＝0，

∴（m－n）²＝0，（n－4）²＝0，

∴n＝4，m＝4．

根据你的观察，探究下面的问题：

(1)、已知x²－2xy＋2y²＋6y＋9＝0，求

x

、

y

的值；

(2)、已知△АВС的三边长分别为а，b，с都是正整数，且满足a²＋b²－10a－12b＋61＝0，求△ABC的边a、b的值；

(3)、已知a－b＝8，ab＋c²－16c＋80＝0，求a＋b＋c的值．

查看试题解析

4. 用平方差公式进行因式分解在数的运算中有着广泛的应用，比如，数的整除性探究中的应用．

例： $2008^{3} - 2008$ 能被2009整除吗？

解: $2008^{3} - 2008 = 2008 (2008^{2} - 1) = 2008 (2008 + 1) (2008 - 1) = 2008 \times 2009 \times 2007$

∵ $2008^{3} - 2008$ 中有因数2009，

∴ $2008^{3} - 2008$ 一定能被2009整除．

请你试一试：已知数字 $(2^{48} - 1)$ 恰能被两个在60和70之间的整数整除，求出这两个数．

查看试题解析

5. 发现与探索．

(1)、根据小明的解答（图1）将下列各式因式分解

①a²﹣12a+20

②a²﹣6ab+5b²

(2)、根据小丽的思考（图2）解决问题．

试说明：代数式a²﹣12a+20的最小值为﹣16．

查看试题解析

6. 探究：如何把多项式x²+8x+15因式分解？

(1)、观察：上式能否可直接利用完全平方公式进行因式分解？答：；

(2)、（阅读与理解）：由多项式乘法，我们知道(x+a)(x+b)=x²+(a+b)x+ab ，将该式从右到左地使用，即可对形如x²+(a+b)x+ab的多项式进行因式分解，即：

x²+(a+b)x+ab=(x+a)(x+b)

此类多项式x²+(a+b)x+ab的特征是二次项系数为1，常数项为两数之积，一次项系数为这两数之和．

猜想并填空：x²+8x+15=x²+[()+()]x+()×()=(x+)(x+)

(3)、上面多项式x²+8x+15的因式分解是否符合题意，我们需要验证．请写出验证过程．

(4)、请运用上述方法将下列多项式进行因式分解：

① x²+8x+12 ② x²-x-12

查看试题解析

7. 阅读以下材料，并解决问题：

常用的分解因式的方法有提取公因式法、公式法等，但有的多项式则不能直接用上述两种方法进行分解，比如多项式． $x^{2} - 4 y^{2} - 2 x + 4 y$ ．这样我们就需要结合式子特点，探究新的分解方法．仔细观察这个四项式，会发现：若把它的前两项结合为一组符合平方差公式特点，把它的后两项结合为一组可提取公因式，而且对前后两组分别进行因式分解后会出现新的公因式，提取新的公因式就可以完成对整个式子的因式分解．具体过程如下：

例1： $x^{2} - 4 y^{2} - 2 x + 4 y$

$= (x^{2} - 4 y^{2}) - (2 x - 4 y)$ ……………………分成两组

$= (x + 2 y) (x - 2 y) - 2 (x - 2 y)$ ………………分别分解

$= (x - 2 y) (x + 2 y - 2)$ ………………………提取公因式完成分解

像这种将一个多项式适当分组后，进行分解因式的方法叫做分组分解法．分组分解法一般是针对四项或四项以上的多项式，关键在恰当分组，分组须有“预见性”，预见下一步能继续分解，直到完成分解．

(1)、材料例1中，分组的目的是．

(2)、若要将以下多项式进行因式分解，怎样分组比较合适？

$x^{2} - y^{2} + x + y =$ ；

$2 a + a^{2} - 2 b - 2 a b + b^{2} =$ ．

(3)、利用分组分解法进行因式分解：

x^{2} - 2 x y + y^{2} - 4

．

查看试题解析

8. 如果一个自然数能表示为两个自然数的平方差，那么称这个自然数为智慧数，例如：

16=5²﹣3² ， 16就是一个智慧数，小明和小王对自然数中的智慧数进行了如下的探索：

小明的方法是一个一个找出来的：

0=0²﹣0² ， 1=1²﹣0² ， 3=2²﹣1² ，

4=2²﹣0² ， 5=3²﹣2² ， 7=4²﹣3² ，

8=3²﹣1² ， 9=5²﹣4² ， 11=6²﹣5² ， …

小王认为小明的方法太麻烦，他想到：

设k是自然数，由于（k+1）²﹣k²=（k+1+k）（k+1﹣k）=2k+1．

所以，自然数中所有奇数都是智慧数．

问题：

(1)、根据上述方法，自然数中第12个智慧数是；

(2)、他们发现0，4，8是智慧数，由此猜测4k（k≥3且k为正整数）都是智慧数，请你参考小王的办法证明4k（k≥3且k为正整数）都是智慧数．

(3)、他们还发现2，6，10都不是智慧数，由此猜测4k+2（k为自然数）都不是智慧数，请利用所学的知识判断26是否是智慧数，并说明理由．

查看试题解析

9. 探究题：

(1)、问题情景：将下列各式因式分解，将结果直接写在横线上：

$x^{2} + 6 x + 9 =$ ； $x^{2} - 4 x + 4 =$ ； $4 x^{2} - 20 x + 25 =$ ；

(2)、探究发现：观察以上三个多项式的系数，我们发现：

6^{2} = 4 \times 1 \times 9

；

(- 4)^{2} = 4 \times 1 \times 4

；

(- 20)^{2} = 4 \times 4 \times 25

；

归纳猜想：若多项式 $a x^{2} + b x + c (a > 0 ， c > 0)$ 是完全平方式，猜想：系数a，b，c之间存在的关系式为．

(3)、验证结论：请你写出一个不同于上面出现的完全平方式，并用此式验证你猜想的结论．

(4)、解决问题：若多项式

(n + 1) x^{2} - (2 n + 6) x + (n + 6)

是一个完全平方式，利用你猜想的结论求出n的值．

查看试题解析

10. 一些含根号的式子可以写成另一个式子的平方，如3+2

\sqrt{2}

＝（1+

\sqrt{2}

）².设a+b

\sqrt{2} = (m + n \sqrt{2})^{2}

（其中a、b、m、n均为正整数），则有a+b

\sqrt{2}

＝m²+2n²+2mn

\sqrt{2}

， ∴a＝m²+2n² ， b＝2mn.这样可以把部分a+b

\sqrt{2}

的式子化为平方式的方法.请你仿照上述的方法探索并解决下列问题：

(1)、当a、b、m、n均为正整数时，若a+b

\sqrt{3}

＝（m+n

\sqrt{3}

）² ，用含m、n的式子分别表示a、b，得：a＝， b＝.

(2)、利用所探索的结论，找一组正整数a、b、m、n填空：+

\sqrt{5}

＝（+

\sqrt{5}

）²；

(3)、化简

\frac{1}{\sqrt{16 - 6 \sqrt{7}}} - \frac{1}{\sqrt{11 + 4 \sqrt{7}}}

查看试题解析

11. 提出问题：你能把多项式

x^{2} + 5 x + 6

因式分解吗？

探究问题：如图1所示，设a，b为常数，由面积相等可得： $(x + a) (x + b) = x^{2} + a x + b x + a b$ $= x^{2} + (a + b) x + a b$ ，将该式从右到左使用，就可以对形如 $x^{2} + (a + b) x + a b$ 的多项式进行因式分解即 $x^{2} + (a + b) x + a b = (x + a) (x + b)$ ．观察多项式 $x^{2} + (a + b) x + a b$ 的特征是二次项系数为1，常数项为两数之积，一次项为两数之和．

解决问题： $x^{2} + 5 x + 6 = x^{2} + (2 + 3) x + 2 \times 3 = (x + 3) (x + 2)$ ．

运用结论：

(1)、基础运用：把多项式

x^{2} + 4 x - 21

进行因式分解．

(2)、知识迁移：对于多项式

4 x^{2} - 4 x - 15

进行因式分解还可以这样思考：

将二次项 $4 x^{2}$ 分解成如图2所示中的两个 $2 x$ 的积，再将常数项 $- 15$ 分解成 $- 5$ 与3的乘积，图中的对角线上的乘积的和为 $- 4 x$ ，就是 $4 x^{2} - 4 x - 15$ 的一次项，所以有 $4 x^{2} - 4 x - 15 = (2 x - 5) (2 x + 3)$ ．这种分解因式的方法叫做“十字相乘法”．

请用十字相乘法进行因式分解：① $3 x^{2} - 19 x - 14$ ；② $6 a^{2} - 13 a b + 6 b^{2}$ ．

查看试题解析

12. 数与形是数学研究的两大部分，它们间的联系称为数形结合，数形结合大致分为两种情形，或者借助图形的直观来阐明数之间的关系，或者借助数的精确性来阐明图形的属性，即“以形助数”或“以数解形”，整式乘法中也利用图形面积来论证数量关系．现用砖块相同的面（如材料图，长为a，宽为b的小长方形）拼出以下图形，延长部分边框，则把这些拼图置于如图所示的正方形或大长方形内，请解答下列问题．

(1)、求图1中空白部分的面积

S_{1}

（用含

a b

的代数式表示）．

(2)、图1，图2中空白部分面积

S_{1}

、

S_{2}

分别为19、68，求

a b

值．

(3)、图3中空白面积为S，根据图形中的数量关系，将下列式子因式分解：

① $S_{3} + 7 a b =$ ；

② $S_{3} - a^{2} + 5 a b =$ ．

查看试题解析

13. [数学实验探索活动]

实验材料现有若干块如图①所示的正方形和长方形硬纸片.

实验目的：

用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径.

例如，选取正方形、长方形硬纸片共6块，拼出一个如图②的长方形，计算它的面积，写出相应的等式有a²+3ab+2b²=（a+2b）（a+b）或（a+2b）（a+b）=a²+3ab+2b².

问题探索：

(1)、小明想用拼图的方法解释多项式乘法（2a+b）（a+b）=2a²+3ab+b² ，那么需要两种正方形纸片张，长方形纸片张；

(2)、选取正方形、长方形硬纸片共8块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；

(3)、试借助拼图的方法，把二次三项式2a²+5ab+2b²分解因式，并把所拼的图形画在虚线方框3内.

查看试题解析

14. 我们常利用数形结合思想探索整式乘法的一些法则和公式.类似地，我们可以借助一个棱长为

a

的大正方体进行以下探索：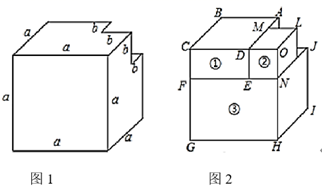

(1)、在大正方体一角截去一个棱长为

b (b < a)

的小正方体，如图1所示，则得到的几何体的体积为；

(2)、将图1中的几何体分割成三个长方体①、②、③，如图2所示，∵

B C = a

，

A B = a - b

，

C F = b

，∴长方体①的体积为

a b (a - b)

.

类似地，长方体②的体积为，长方体③的体积为；（结果不需要化简）

(3)、将表示长方体①、②、③的体积相加，并将得到的多项式分解因式的结果为；

(4)、用不同的方法表示图1中几何体的体积，可以得到的等式为.

(5)、已知

a - b = 4

，

a b = 2

，求

a^{3} - b^{3}

的值.

查看试题解析

15. 实验材料：现有若干块如图①所示的正方形和长方形硬纸片.实验目的：用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径.例如，选取正方形、长方形硬纸片共6块，拼出一个如图②的长方形，计算它的面积写出相应的等式有

a^{2} + 3 a b + 2 b^{2} = (a + 2 b) (a + b)

或

(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}

.

探索问题：

(1)、选取图①所示的正方形、长方形硬纸片共8块可以拼出一个如图②的长方形，计算图②的面积，并写出相应的等式；

(2)、试借助拼图的方法，把二次三项式

2 a^{2} + 5 a b + 2 b^{2}

分解因式，并把所拼的图形画在方框内.

(3)、小明同学又用了

x

张边长为

a

的正方形，

y

张边长为

b

的正方形，

z

张边长为

a

，

b

的长方形纸片拼出了一个面积为

(25 a + 7 b) (18 a + 45 b)

的长方形，那么

x + y + z

的值为.

查看试题解析

备考2024年中考数学探究性训练专题5 因式分解

一、综合题