备考2024年中考数学探究性训练专题2 图形规律

试卷更新日期：2024-03-10 类型：二轮复习

进入出卷网下载

一、选择题

1. 根据图中箭头的指向规律，从2022到2023再到2024，箭头的方向是图示中的（）

A、 B、 C、 D、

查看试题解析
2. 用围棋子按下面的规律摆放图形，则摆放第 $2023$ 个图形需要围棋子的枚数是（）

A、 $4047$ B、 $6069$ C、 $6070$ D、 $6071$

查看试题解析
3. 如果一个等腰三角形的顶角为36°，那么其底边与腰之比等于 $\frac{\sqrt{5 - 1}}{2}$ ，我们把这样的等腰三角形称为黄金三角形．如图，在△ABC中，AB=AC=1，∠A=36°，△ABC看作第一个黄金三角形；作∠ABC的平分线BD，交AC于点D，△BCD看作第二个黄金三角形；作∠BCD的平分线CE，交BD于点E，△CDE看作第三个黄金三角形；…以此类推，第2023个黄金三角形的腰长是（　　）

A、 ${(\frac{\sqrt{5} - 1}{2})}^{2022}$ B、 ${(\frac{\sqrt{5} - 1}{2})}^{2021}$ C、 ${(\frac{3 + \sqrt{5}}{2})}^{2020}$ D、 ${(\frac{3 + \sqrt{5}}{2})}^{2019}$

查看试题解析
4. 用圆圈按如图所示的规律拼图案，其中第1个图案中有2个圆圈，第2个图案中有5个圆圈，第3个图案中有8个圆圈，第4个图案中有11个圆圈，…，按此规律排列下去，则第7个图案中圆圈的个数为（）

A、14 B、20 C、23 D、26

查看试题解析
5. 将一个正方形剪成n个小正方形，第一次操作按照图1所示，分割出4个正方形，第二次操作按如图2所示，分割出6个正方形，第三次操作按如图3所示，按照上述规律，则第n次操作，正方形的个数为（）

A、（n+1）² B、3n+1 C、2n D、2n+2

查看试题解析
6. 如图，在平面直角坐标系中，将边长为1的正方形 $O A B C$ 绕点 $O$ 顺时针旋转45°后得到正方形 $O A_{1} B_{1} C_{1}$ ，依此方式，绕点 $O$ 连续旋转2023次得到正方形 $O A_{2023} B_{2023} C_{2023}$ ，那么点 $A_{2023}$ 的坐标是（）

A、 $(1 ， 0)$ B、 $(0 ， - 1)$ C、 $(\frac{\sqrt{2}}{2} ， - \frac{\sqrt{2}}{2})$ D、 $(- \frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$

查看试题解析
7. 如图，在平面直角坐标系中， $△ O A B$ 的顶点 $O$ 在原点上， $O A$ 边在 $x$ 轴的正半轴上， $A B ⊥ x$ 轴， $A B = 1$ ， $∠ A O B = 30 °$ ，将 $△ O A B$ 绕点 $O$ 顺时针旋转，每次旋转90°，则第2023次旋转结束时，点 $B$ 的坐标为（）

A、 $(1 ， \sqrt{3})$ B、 $(1 ， - \sqrt{3})$ C、 $(- \sqrt{3} ， 1)$ D、 $(- 1 ， \sqrt{3})$

查看试题解析
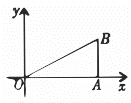8. 如图，在平面直角坐标系中，边长为2的正六边形 $A B C D E F$ 的中心与原点O重台， $A B ∥ x$ 轴，交y轴于点P．将 $△ O A P$ 绕点O逆时针旋转，每次旋转 $90 °$ ，则第2023次旋转结束时，点A的坐标为（）

A、 $(\sqrt{3} ， - 1)$ B、 $(- 1 ， - \sqrt{3})$ C、 $(- \sqrt{3} ， 1)$ D、 $(1 ， \sqrt{3})$

查看试题解析
9. 如图是一组有规律的图案，它们由边长相等的等边三角形组成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形，……，照此规律，摆成第6个图案需要的三角形个数是（）

A、19个 B、22个 C、25个 D、26个

查看试题解析
10. 如图，在矩形ABCD中，AB＝1，BC＝2，连接AC ，以对角线AC为边，按逆时针方向作矩形ACC₁B₁ ，使矩形ACC₁B₁∽矩形ADCB；再连接AC₁ ，以对角线AC₁为边，按逆时针方向作矩形AC₁C₂B₂ ，使矩形AC₁C₂B₂∽矩形ACC₁B₁ ， …，按照此规律作下去，则边AC₂₀₂₂的长为（　　）

A、 $\sqrt{5} \times {(\frac{\sqrt{5}}{2})}^{2022}$ B、 $2 \times {(\frac{\sqrt{5}}{2})}^{2021}$ C、 $\sqrt{5} \times 2^{2022}$ D、 $\sqrt{5} \times {(\frac{\sqrt{5}}{2})}^{2021}$

查看试题解析

二、填空题

11. 如图，把同样大小的黑色棋子摆放在正多边形的边上，第一个图形需要3个黑色棋子，第二个图形需要8个黑色棋子……，按照这样的规律摆下去，第 $n$ （n是正整数）个图形需要黑色棋子的个数是（用含n的代数式表示）．

查看试题解析
12. 如图，在正方形ABCB₁中，AB＝1，AB与直线l的夹角为30°，延长CB₁交直线l于点A₁ ，作正方形A₁B₁C₁B₂ ，延长C₁B₂交直线l于点A₂ ，作正方形A₂B₂C₂B₃；延长C₂B₃交直线l于点A₃ ， …，依此规律，则A₂₀₂₃B₂₀₂₃＝．

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 2$ ， $B C = 4$ ，点 $M_{1} ， N_{1} ， P_{1}$ 分别在 $A C$ 、 $B C$ 、 $A B$ 上，且四边形 $M_{1} C N_{1} P_{1}$ 是正方形，点 $M_{2} ， N_{2} ， P_{2}$ 分别在 $P_{1} N_{1} 、 B N_{1} 、 B P_{1}$ 上，且四边形 $M_{2} N_{1} N_{2} P_{2}$ 是正方形……，点 $M_{n} ， N_{n} ， P_{n}$ 分别在 ${P_{n}}_{－ 1} {N_{n}}_{－ 1} ， B {N_{n}}_{－ 1} ， B {P_{n}}_{－ 1}$ 上，且四边形 $M_{n} {N_{n}}_{－ 1} N_{n} P_{n}$ 是正方形，则线段 $M_{2022} P_{2022}$ 的长度是．

查看试题解析
14. “勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为．

查看试题解析
15. 如图，等腰 $R t △ O A_{1} A_{2}$ ， $O A_{1} = A_{1} A_{2} = 1$ ，以OA₂为直角边作Rt $△ O A_{2} A_{3}$ ，再以OA₃为直角边作Rt $△ O A_{3} A_{4}$ ，以此规律作等腰Rt $△ O A_{8} A_{9}$ ，则 $△ O A_{8} A_{9}$ 的面积是

查看试题解析
16. 如图，A₁ ， A₂ ， A₃ ， A₄ ， …An，A_n+1是直线y＝ $\frac{1}{2}$ x+2上的点，分别过点A₁ ， A₂ ， A₃ ， A₄ ， …A_n ， A_n+1作x轴的垂线，垂足分别为B₁ ， B₂ ， B₃ ， B₄ ， …B_n ， B_n+1已知OB₁＝B₁B₂＝B₂B₃＝B₃B₄＝…＝B_nB_n+1＝1，连接A₁B₂ ， B₁A₂和A₂B₃ ， B₂A₃ ， …A_nB_n+1依次相交于点P₁ ， P₂ ， P₃ ， …P_N ， △A₁B₁P₁ ， △A₂B₂P₂ ， △A₃B₃P₃ ， …，△A_NB_NP_N的面积依次为S₁ ， S₂ ， S₃ ， …S_N ，则S_n等于．

查看试题解析

三、实践探究题

17. 【观察思考】

(1)、【规律发现】请用含n的式子填空：
第n个图案中“◎”的个数为.

(2)、第1个图案中“★”的个数可表示为 $\frac{1 \times 2}{2}$ ，第2个图案中“★”的个数可表示为 $\frac{2 \times 3}{2}$ ，第3个图案中“★”的个数可表示为 $\frac{3 \times 4}{2}$ ，第4个图案中“★”的个数可表示为 $\frac{4 \times 5}{2} ， ⋯ ⋯$ ，第 $n$ 个图案中“★”的个数可表示为.

(3)、【规律应用】
结合图案中“★”的排列方式及上述规律，求正整数n，使得连续的正整数之和1+2＋3＋……+n等于第n个图案中“◎”的个数的2倍.

查看试题解析

18. 如图，

n + 1

个边长为2的等边三角形有一条边在同一直线上，设

△ B_{2} D_{1} C_{1}

的面积为

S_{1}

，

△ B_{3} D_{2} C_{2}

的面积为

S_{2}

，

△ B_{n + 1} D_{n} C_{n}

的面积为

S_{n}

．

(1)、【规律探究】：

探究一

探究二

探究三

∵ $△ B_{1} B_{2} D_{1} ∽ △ C_{1} A D_{1}$ ，

∴ $B_{1} D_{1} ： D_{1} C_{1} = 1 ： 1$ ，

∴ $S_{1} =$ ．

∵ $B_{2} B_{3} ： A C_{2} = 1 ： 2$ ，

∴ $B_{2} D_{2} ： D_{2} C_{2} = 1 ： 2$ ，

∴ $S_{2} =$ ， $S_{1} =$ ．

∵ $B_{3} B_{4} ： A C_{3} = 1 ： 3$ ，

∴ $B_{3} D_{3} ： D_{3} C_{3} = 1 ： 3$ ，

∴ $S_{3} =$ ， $S_{2} =$ ．

(2)、【结论归纳】

$S_{n} =$ ．（用含n的式子表示）

查看试题解析

19. 【观察思考】
【规律发现】
请用含 $n$ 的式子填空：

(1)、第 $n$ 个图案中“ $◎$ ”的个数为；

(2)、第 $1$ 个图案中“ $★$ ”的个数可表示为 $\frac{1 \times 2}{2}$ ，第 $2$ 个图案中“ $★$ ”的个数可表示为 $\frac{2 \times 3}{2}$ ，第 $3$ 个图案中“ $★$ ”的个数可表示为 $\frac{3 \times 4}{2}$ ，第 $4$ 个图案中“ $★$ ”的个数可表示为 $\frac{4 \times 5}{2}$ ， $\dots \dots$ ，第 $n$ 个图案中“ $★$ ”的个数可表示为．

(3)、【规律应用】
结合图案中“ $★$ ”的排列方式及上述规律，求正整数 $n$ ，使得连续的正整数之和 $1 + 2 + 3 + \dots \dots + n$ 等于第 $n$ 个图案中“ $◎$ ”的个数的 $2$ 倍．

查看试题解析
20. 阅读材料，解决问题.
相传古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题.他们在沙滩上画点或用小石子来表示数，比如，他们研究过1、3、6、10…，由于这些数可以用图中所示的三角点阵表示，他们就将每个三角点阵中所有的点数和称为三角数.

则第 $n$ 个三角数可以用 $1 + 2 + 3 + \dots + (n - 2) + (n - 1) + n =$ $\frac{n (n + 1)}{2} (n \geq 1$ 且为整数）来表示.

(1)、若三角数是55，则n=；

(2)、把第n个三角点阵中各行的点数依次换为 $2 ， 4 ， 6 ， \dots$ ， $2 n ， \dots$ ，请用含 $n$ 的式子表示前 $n$ 行所有点数的和；

(3)、在（2）中的三角点阵中前 $n$ 行的点数的和能为120吗?如果能，求出 $n$ ，如果不能，请说明理由.

查看试题解析
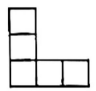
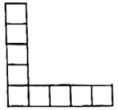
21. 如图，下列图形是由边长为1个单位长度的小正方形按照一定规律摆放的“ $L$ ”形图形，观察图形：

图1 图2 图3

(1)、按此规律，图4中小正方形的数量是个；

(2)、我们把图1中小正方形个数记作 $a_{1}$ ，图2中小正方形图个数记作 $a_{2} ， \cdot \cdot \cdot$ ，图 $n$ 中小正方形个数记作 $a_{n}$ ，若 $a_{1} + a_{2} + \cdot \cdot \cdot + a_{n} = 165$ ，求 $n$ 的值．

查看试题解析

22. 图形规律

①

②

③

④

序号	$1$	$2$	$3$	$4$	$5$	……
梯形数	$1$	$2$	$4$	$6$	$9$	……	？

如图，按此规律摆放，

(1)、第

6

个图中梯形数为，第

7

个图中梯形数为，第

8

个图中梯形数为，第

9

个图中梯形数为；

(2)、第

(2 n + 2)

个图中梯形数与第

(2 n - 1)

个图中梯形数的差为；

查看试题解析

23. 为了提高动手操作能力，安徽某学校九年级学生利用课后服务时间进行拼图大赛，他们用边长相同的正方形和正三角形进行拼接，赛后整理发现一组有规律的图案，如图所示．
【观察思考】
第1个图案有4个正三角形，第2个图案有7个正三角形，第3个图案有10个正三角形，…依此类推
【规律总结】

(1)、第5个图案有个正三角形

(2)、第n个图案中有个正三角形，（用含n的代数式表示）

(3)、【问题解决】
现有2023个正三角形，若按此规律拼第n个图案，要求正三角形一次用完，则该图案需要正方形多少个？

查看试题解析

24. 18世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式.请你观察下列几种简单多面体模型，解答下列问题.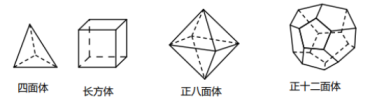

(1)、根据上面的多面体模型，直接写出表格中的m，n的值，则

m =

，

n =

多面体	顶点数（V）	面数（F）	棱数（E）
四面体	4	4	6
长方体	m	6	12
正八面体	n	8	12
正十二面体	20	12	30

(2)、你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是.

(3)、一个多面体的面数等于顶点数，且这个多面体有30条棱，求这个多面体的面数.

查看试题解析

25.

(1)、观察图1所示的点阵图和相应的等式，并在④后面的横线上写出相应的等式.
①1=1；
② $1 + 2 = \frac{(1 + 2) \times 2}{2} = 3 ；$
③ $1 + 2 + 3 = \frac{(1 + 3) \times 3}{2} = 6 ；$
④；
...

(2)、结合(1)观察图2所示的点阵图和相应的等式，并在⑤后面的横线上写出相应的等式.
① $1 = 1^{2} ；$
② $1 + 3 = 2^{2} ；$
③ $3 + 6 = 3^{2} ；$
④ $6 + 10 = 4^{2} ；$
⑤；
...

(3)、请通过猜想，写出(2)中与第n个点阵图相对应的等式。

查看试题解析
26. （问题）用n边形的对角线把n边形分割成（n-2个三角形，共有多少种不同的分割方案 $(n \geq 4)$ ？
（探究）为了解决上面的数学问题，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进转化，最后猜想得出结论．不妨假设n边形的分割方案有 $f (n)$ 种．

探究一：用四边形的对角线把四边形分割成2个三角形，共有多少种不同的分割方案？如图①，图②，显然，只有2种不同的分割方案．所以， $f (4) = 2$ ．

探究二：用五边形的对角线把五边形分割成3个三角形，共有多少种不同的分割方案？不妨把分割方案分成三类：

第1类：如图③，用点 $A$ ， $E$ 与 $B$ 连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有 $f (4)$ 种不同的分割方案，所以，此类共有 $f (4)$ 种不同的分割方案．

第2类：如图④，用点 $A$ ， $E$ 与 $C$ 连接，把五边形分割成3个三角形，有1种不同的分割方案，可视为 $\frac{1}{2} f (4)$ 种分割方案．

第3类：如图⑤，用点 $A$ ， $E$ 与 $D$ 连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有f（4）种不同的分割方案，所以，此类共有f（4）种不同的分割方案．

所以， $f (5) = f (4) + \frac{1}{2} f (4) + f (4) = \frac{5}{2} \times f (4) = \frac{10}{4} \times f (4) = 5$ （种）

探究三：用六边形的对角线把六边形分割成4个三角形，共有多少种不同的分割方案？不妨把分割方案分成四类：

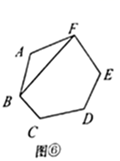
第1类：如图⑥，用 $A$ ， $F$ 与 $B$ 连接，先把六边形分割转化成1个三角形和1个五边形，再把五边形分割成3个三角形，由探究二知，有 $f (5)$ 种不同的分割方案，所以，此类共有 $f (5)$ 种不同的分割方案．

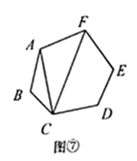
第2类：如图⑦，用 $A$ ， $F$ 与 $C$ 连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有 $f (4)$ 种不同的分割方案．所以，此类共有 $f (4)$ 种分割方案．

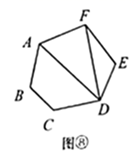
第3类：如图⑧，用 $A$ ， $F$ 与 $D$ 连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有 $f (4)$ 种不同的分割方案．所以，此类共有 $f (4)$ 种分割方案．

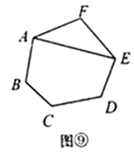
第4类：如图，用 $A$ ， $F$ 与 $E$ 连接，先把六边形分割转化成1个三角形和1个五边形，再把五边形分割成3个三角形，由探究二知，有 $f (5)$ 种不同的分割方案．所以，此类共有 $f (5)$ 种分割方案．

所以， $f (6) = f (5) + f (4) + f (4) + f (5)$

$= f (5) + \frac{2}{5} f (5) + \frac{2}{5} f (5) + f (5) = \frac{14}{5} \times f (5) = 14$ （种）

探究四：用七边形的对角线把七边形分割成5个三角形，则 $f (7)$ 与 $f (6)$ 的关系为 $f (7) = \frac{()}{6} \times f (6)$ ，共有种不同的分割方案．

……

（结论）用 $n$ 边形的对角线把 $n$ 边形分割成 $(n - 2)$ 个三角形，共有多少种不同的分割方案 $(n \geq 4)$ ？（直接写出 $f (n)$ 与 $f (n - 1)$ 之间的关系式，不写解答过程）

（应用）用九边形的对角线把九边形分割成7个三角形，共有多少种不同的分割方案？（应用上述结论中的关系式求解）

查看试题解析
27. 为迎接七一建党节，某社区党委在广场上设计了一座三角形展台，需在它的每条边上摆放上相等盆数的鲜花进行装饰．若每条边上摆放两盆鲜花，共需要3盆鲜花；若每条边上摆放3盆鲜花，共需要6盆鲜花；……，按此要求摆放下去（如图所示，每个小圆圈表示一盆鲜花）．

(1)、填写下表：
每条边上摆放的盆数（n）
2
3
4
5
6
…
需要的鲜花总盆数（y）
3
6
9
…

(2)、写出需要的鲜花总盆数y与n之间的关系式：

(3)、能否用2023盆鲜花作出符合要求的摆放？如果能，请计算出每条边上应摆放的盆数；如果不能，请说明理由．

查看试题解析
28. [问题提出]如图1，由 $n \times n \times n$ （长×宽×高）个小立方块组成的正方体中，到底有多少个长方体（包括正方体）呢？

[问题探究]我们先从较为简单的情形入手．

如图2，由 $2 \times 1 \times 1$ 个小立方块组成的长方体中，长共有 $1 + 2 = \frac{2 \times 3}{2} = 3$ 条线段，宽和高分别只有1条线段，所以图中共有 $3 \times 1 \times 1 = 3$ 个长方体．

如图3，由 $2 \times 1 \times 1$ 个小立方块组成的长方体中，长和宽分别有 $1 + 2 = \frac{2 \times 3}{2} = 3$ 条线段，高有1条线段，所以图中共有 $3 \times 3 \times 1 = 9$ 个长方体．

(1)、如图4，由 $2 \times 2 \times 2$ 个小立方体组成的正方体中，长、宽、高分别有 $1 + 2 = \frac{2 \times 3}{2} = 3$ 条线段，所以图中共有个长方体．

(2)、由 $2 \times 3 \times 6$ 个小立方块组成的长方体中，长共有 $1 + 2 = \frac{2 \times 3}{2} = 3$ 条线段，宽共有条线段，高共有条线段，所以图中共有个长方体．

(3)、[问题解决]由 $n \times n \times n$ 个小立方块组成的正方体中，长、宽、高各有条线段，所以图中共有个长方体．

(4)、[结论应用]如果由若干个小立方块组成的正方体中共有1000个长方体，那么组成这个正方体的小立方块的个数是多少？请通过计算说明你的结论．

查看试题解析

每条边上摆放的盆数（n）	2	3	4	5	6	…
需要的鲜花总盆数（y）	3	6	9			…