备考2024年中考数学探究性训练专题1 数、式规律
试卷更新日期:2024-03-10 类型:二轮复习
一、选择题
-
1. 观察下列两行数:
1,3,5,7,9,11,13,15,17,…
1,4,7,10,13,16,19,22,25,…
探究发现:第1个相同的数是1,第2个相同的数是7,…,若第n个相同的数是103,则n等于( )
A、18 B、19 C、20 D、212. 观察下列关于x的单项式,探究其规律:x,3x2 , 5x3 , 7x4 , 9x5 , 11x6 , ….按照上述规律,第2021个单项式是( )A、2021x2021 B、4041x2022 C、4041x2021 D、4043x20213. 在“点燃我的梦想,数学皆有可能”数学创新设计活动中,小强设计了一个数学探究活动,他对依次排列的两个整式和按如下规律进行操作:第1次操作后得到3个整式 , , ;第2次操作后得到4个整式 , , , ……其操作规则为:每次操作所增加的整式,都是用上一次操作得到的最后一个整式减去其前一整式的差,小强将这个活动命名为“回头差”游戏.则该“回头差”游戏的第2023次操作后得到的各整式之和是( )A、 B、 C、 D、4. 如图,在平面直角坐标系中, , , , ……根据这个规律,探究可得点 的坐标是( )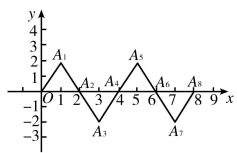 A、 B、 C、 D、5. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中,把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方.请你探究如图洛书三阶幻方中,奇数和偶数的位置、数和数之间的数量关系所呈现的规律,根据这一规律,求出 , , 则( )
A、 B、 C、 D、5. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中,把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方.请你探究如图洛书三阶幻方中,奇数和偶数的位置、数和数之间的数量关系所呈现的规律,根据这一规律,求出 , , 则( )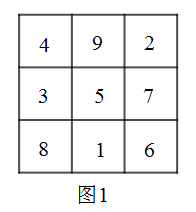
 A、16 B、8 C、 D、6. 如果正整数a、b、c满足等式 ,那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
A、16 B、8 C、 D、6. 如果正整数a、b、c满足等式 ,那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )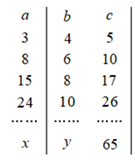 A、47 B、62 C、79 D、987. 仔细观察,探究规律:
A、47 B、62 C、79 D、987. 仔细观察,探究规律:则算式 值的个位数字为( )
A、1 B、3 C、5 D、7二、填空题
-
8. 小苗探究了一道有关分式的规律题, , , , , , , , …请按照此规律在横线上补写出第6个分式.9. 两小朋友在玩上楼梯游戏,规定一步只能上一级或二级台阶,玩着玩着两人发现:当楼梯的台级数为一级、二级、三级、…逐步增加时,楼梯的上法依次为:1,2,3,5,8,13,21,…(这就是著名的斐波拉契数列),请你认真观察这一列数规律,探究一下,上11级台阶共有种上法.10. 观察下列两行数,探究第②行数与第①行数的关系:
-2,4,-8,16,-32,64,…①
0,7,-4,21,-26,71,…②
根据你的发现,完成填空:第①行数的第10个数为;取每行数的第2023个数,则这两个数的和为.
11. 下列是一些两位数减法运算:,
观察上述算式及其计算结果,对两位数减法运算中的某种特殊情形进行探究:
(1)、请另外写出一个符合上述规律的算式:;(2)、用字母表示你所观察到的规律 .12. 小亮在计算的值时,把的值看错了,其结果等于25,细心的小敏把正确的的值代入计算, 其结果也是25.为了探究明白,她又把代入,结果还是25.则的值为 .13. 已知、、为非零有理数,请你探究以下问题:(1)、当时,;(2)、的最小值为 .三、解答题
-
14. 发现:当两个不同的正整数同为偶数或奇数时,这两个数之和与这两个数之差的平方差一定能被4整除,且这两个数的积可以表示为两个正整数的平方差.
验证:如,能被4整除,请把3与1的积写成两个正整数的平方差;
探究:设“发现”中两个正整数分别为m,n,请论证“发现”中的结论正确.
15. 小颖利用平方差公式,自己探究出一种解某一类根式方程的方法.下面是她解方程 + =5的过程.解:设 ﹣ =m,与原方程相乘得:
( + )×( )=5m,
x﹣2﹣(x﹣7)=5m,解之得m=1,
∴ ﹣ =1,与原方程相加得:
( + )+( )=5+1,
2 =6,解之得,x=11,经检验,x=11是原方程的根.
学习借鉴解法,解方程 ﹣ =1.
16. 学习完数轴以后,喜欢探索的小聪在纸上画了一个数轴(如图所示),并进行下列操作探究:(1)、操作一:折叠纸面,使表示1的点与表示-1的点重合,则表示-4的点与表示的点重合.(2)、操作二:折叠纸面,使表示-3的点与表示1的点重合,回答以下问题:表示2的点与表示的点重合;
(3)、若数轴上A、B两点之间距离是a(a>0)(A在B的左侧),且折叠后A、B两点重合.求A、B两点表示的数是多少?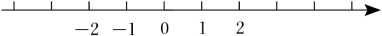 17. 探究题:阅读下列材料,规定一种运 , 例如 , 再如 , 按照这种运算的规定,请解答下列问题:(1)、 . (只填结果);(2)、若 , 求的值.(写出解题过程)(3)、若化简后是一个关于x的一元一次方程,求k的值.(写出解题过程)18. 数学老师在课堂上提出一个问题:“通过探究知道: , 它是个无限不循环小数,也叫无理数,它的整数部分是 , 那么有谁能说出它的小数部分是多少?”,小明举手回答:它的小数部分我们无法全部写出来,但可以用来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法现请你根据小明的说法解答:
17. 探究题:阅读下列材料,规定一种运 , 例如 , 再如 , 按照这种运算的规定,请解答下列问题:(1)、 . (只填结果);(2)、若 , 求的值.(写出解题过程)(3)、若化简后是一个关于x的一元一次方程,求k的值.(写出解题过程)18. 数学老师在课堂上提出一个问题:“通过探究知道: , 它是个无限不循环小数,也叫无理数,它的整数部分是 , 那么有谁能说出它的小数部分是多少?”,小明举手回答:它的小数部分我们无法全部写出来,但可以用来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法现请你根据小明的说法解答:
(1)、的小数部分是 , 的整数部分是 , 求的值.
(2)、已知 , 其中是一个整数, , 求的值.19. 探究与应用我们学习过(x-1)(x+1)=x2-1,那么(x-1)(x6+x5+x4+x3+x2+x+1)计算结果呢?
完成下面的探究:
(1)、(x-1)(x2+x+1)=;(2)、(x-1)(x3+x2+x+1)=;……(3)、(x-1)(x6+x5+x4+x3+x2+x+1)=;(4)、应用:计算2+22+23+24+……+22022 .20. 探究题:(1)、问题情景:将下列各式因式分解,将结果直接写在横线上:;;;
(2)、探究发现:观察以上三个多项式的系数,我们发现:;;;归纳猜想:若多项式是完全平方式,猜想:系数a,b,c之间存在的关系式为 .
(3)、验证结论:请你写出一个不同于上面出现的完全平方式,并用此式验证你猜想的结论.(4)、解决问题:若多项式是一个完全平方式,利用你猜想的结论求出n的值.21. 小丽根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律,下面是小丽的探究过程,请补充完整:(1)、具体运算,发现规律,第1个等式:;
第2个等式:;
第3个等式:;
第4个等式: .
(2)、观察、归纳,得出猜想.如果n为正整数,用含n的式子表示上述的运算规律为: .
(3)、试证明你的猜想:22. 探究与发现观察下列等式的规律,解答下列问题;
, , , , , …
(1)、第6个等式为 , 第100个等式;(2)、第n个等式为(用含n的代数式表示,n为正整数);(3)、设 , , , …, . 求:的值.23. 综合与探究观察以下各式:
(x﹣y)(x+y)=x2﹣y2 .
(x﹣y)(x2+xy+y2)=x3﹣y3 .
(x﹣y)(x3+x2y+xy2+y3)=x4﹣y4 .
(x﹣y)(x4+x3y+x2y2+xy3+y4)=x5﹣y5 .
请回答以下问题:
(1)、填空:(x﹣y)(x6+x5y+x4y2+x3y3+x2y4+xy5+y6)= .(2)、若n≥2,求证:6n﹣2n一定能被4整除.(3)、求1019﹣1018﹣1017﹣1016﹣…﹣102﹣10﹣1的值.24. 探究应用:(1)、计算:;=;
(2)、(1)中的整式乘法计算结果很简洁,由(1)发现一个新的乘法公式:(a—b)()=()(用含a、b的字母表示);
(3)、下列各项能用(2)中你发现的乘法公式计算的是( )A、 B、 C、 D、(4)、求的值.25. 小丽根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是小丽的探究过程,请补充完整:
(1)、具体运算,发现规律,特例1:
特:2:
特:3:
特例4: . (填写一个符合上述运算特征的例子);
(2)、观察、归纳,得出猜想.如果n为正整数,用含n的式子表示上述的运算规律为:;
(3)、证明你的猜想;(4)、应用运算规律化简:= .26. 乘法公式的探究及应用.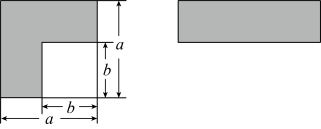 (1)、如左图,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如右图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式)(3)、比较左、右两图的阴影部分面积,可以得到乘法公式(用式子表达)(4)、运用你所得到的公式,计算下列各题:
(1)、如左图,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如右图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式)(3)、比较左、右两图的阴影部分面积,可以得到乘法公式(用式子表达)(4)、运用你所得到的公式,计算下列各题:①
②
(5)、求的值.27. 在数学探究课上,老师布置如下活动:用若干个大小一样的小矩形拼成一个大矩形,探究图中包含的矩形(含正方形)个数,如图1,是由两个小矩形组成的一个图形,该图中共有3个矩形.尝试解决以下问题: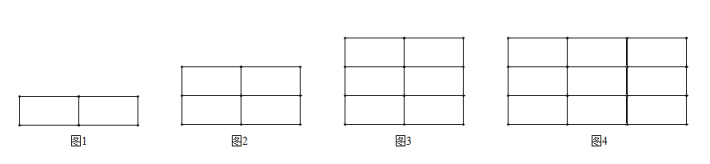 (1)、图2是由4个小矩形组成的图形,该图中共有个矩形;图3是由6个小矩形组成的图形,该图中共有个矩形;(2)、小军在与同学探究时发现,矩形的个数与最大矩形的长和宽所包含的线段条数有关.如图4,最大矩形的长包含6条线段,宽也包含6条线段,则该图中共有个矩形;若某大矩形是由mn个矩形组成,则该图中共有个小矩形;(备注:1+2+3+……+n=)28. 数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
(1)、图2是由4个小矩形组成的图形,该图中共有个矩形;图3是由6个小矩形组成的图形,该图中共有个矩形;(2)、小军在与同学探究时发现,矩形的个数与最大矩形的长和宽所包含的线段条数有关.如图4,最大矩形的长包含6条线段,宽也包含6条线段,则该图中共有个矩形;若某大矩形是由mn个矩形组成,则该图中共有个小矩形;(备注:1+2+3+……+n=)28. 数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依次类推.
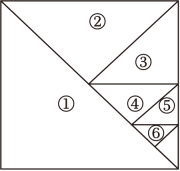 (1)、图中阴影部分的面积为 ;(2)、受此启发,得到=;(3)、联系拓广,得到=(用含n的式子表示);(4)、迁移应用:得到=(直接写出答案即可).29. 实际问题:
(1)、图中阴影部分的面积为 ;(2)、受此启发,得到=;(3)、联系拓广,得到=(用含n的式子表示);(4)、迁移应用:得到=(直接写出答案即可).29. 实际问题:各边长都是整数,最大边长为31的三角形有多少个?
问题建模:为解决上面的数学问题,我们先研究下面的数学模型。
在1~n这n个自然数中,每次取两个数(可重复),使得所取的两个数之和大于n,有多少种不同的取法?
为了找到解决问题的方法,我们把上面数学模型简单化.
探究一:
在1~4这4个自然数中,每次取两个数(可重复),使得所取的两个数之和大于4,有多少种不同的取法?
第一步:在1~4这4个自然数中,每次取两个不同的数,使得所取的两个数之和大于4,根据题意,有下列取法:1+4,2+3,2+4,3+2,3+4,4+1,4+2,4+3;而1+4与4+1,2+3与3+2,…是同一种取法,所有上述每一种取法都重复过一次,因此共有种不同的取法.
第二步:在1~4这4个自然数中,每次取两个相同的数,使得所取的两个数之和大于4,有下列取法:3+3,4+4,因此有2种不同的取法.
综上所述,在1~4这4个自然数中,每次取两个数(可重复),使得所取的两个数之和大于4,有种不同的取法.
探究二:
在1~5这5个自然数中,每次取两个数(可重复),使得所取的两个数之和大于5,有多少种不同的取法?
第一步:在1~5这5个自然数中,每次取两个不同的数,使得所取的两个数之和大于5,根据题意,有下列取法:1+5,2+4,2+5,3+4,3+5,4+2,4+3,4+5,5+1,5+2,5+3,5+4;而1+5与5+1,2+4与4+2,…是同一种取法,所有上述每一种取法都重复过一次,因此共有种不同的取法.
第二步:在1~5这5个自然数中,每次取两个相同的数,使得所取的两个数之和大于5,有下列取法:3+3,4+4,5+5因此有3种不同的取法.
综上所述,在1~5这5个自然数中,每次取两个数(可重复),使得所取的两个数之和大于5,有种不同的取法.
探究三:
在1~6这6个自然数中,每次取两个数(可重复),使得所取的两个数之和大于6,有多少种不同的取法?(仿照探究二写出探究过程)
探究四:
在1~7这7个自然数中,每次取两个数(可重复),使得所取的两个数之和大于7,有 ▲ 种不同的取法.
探究五:
在1~n(n为偶数)这n个自然数中,每次取两个数(可重复),使得所取的两个数之和大于n,有 ▲ 种不同的取法.
探究六:
在1~n(n为奇数)这n个自然数中,每次取两个数(可重复),使得所取的两个数之和大于n,有 ▲ 种不同的取法.
问题解决:
①各边长都是整数,最大边长为20的三角形有 ▲ 个;
②各边长都是整数,最大边长为31的三角形有 ▲ 个.