备考2024年中考数学核心素养专题十二 几何图形的最值问题
试卷更新日期:2024-03-10 类型:二轮复习
一、选择题
-
1. 如图,菱形 , 点、、、均在坐标轴上, , 点 , 点是的中点,点是上的一动点,则的最小值是( )
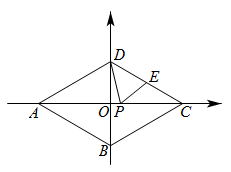 A、3 B、5 C、 D、2. 如图,在中, , , , 且 , 若 , 点是线段上的动点,则的最小值是( )
A、3 B、5 C、 D、2. 如图,在中, , , , 且 , 若 , 点是线段上的动点,则的最小值是( )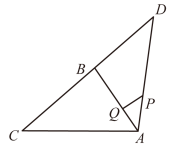 A、 B、 C、 D、3. 如图,AB为⊙O的直径,AB=10,点C是AB上方半圆上的一点,点D是AB下方半圆上的点.连接AC,BC,AD,过点D作DE∥AB交CB的延长线于点E.若AD= , 则当下列哪种情况时,AC•CE取得最大值. ( )
A、 B、 C、 D、3. 如图,AB为⊙O的直径,AB=10,点C是AB上方半圆上的一点,点D是AB下方半圆上的点.连接AC,BC,AD,过点D作DE∥AB交CB的延长线于点E.若AD= , 则当下列哪种情况时,AC•CE取得最大值. ( )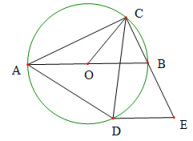 A、CD取最大值时 B、AC⊥AD时 C、CD⊥DE时 D、OC⊥AB时4. 如图,▱ABCD中,AB=3,AD=5,AC⊥AB , E、F为线段BD上两动点(不与端点重合)且EF=BD , 连接AE , CF , 当点EF运动时,对AE+CF的描述正确的是( )
A、CD取最大值时 B、AC⊥AD时 C、CD⊥DE时 D、OC⊥AB时4. 如图,▱ABCD中,AB=3,AD=5,AC⊥AB , E、F为线段BD上两动点(不与端点重合)且EF=BD , 连接AE , CF , 当点EF运动时,对AE+CF的描述正确的是( )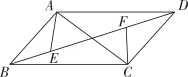 A、等于定值5- B、有最大值 C、有最小值 D、有最小值5. 如图,AB为⊙O的直径,AB=8,点C为半圆AB上一动点,以BC为边向⊙O外作正ΔBCD(点D在直线AB的上方),连接OD,则线段OD的( )
A、等于定值5- B、有最大值 C、有最小值 D、有最小值5. 如图,AB为⊙O的直径,AB=8,点C为半圆AB上一动点,以BC为边向⊙O外作正ΔBCD(点D在直线AB的上方),连接OD,则线段OD的( )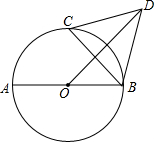 A、随点C的运动而变化,最小值为
A、随点C的运动而变化,最小值为 B、随点C的运动而变化,最大值为8
C、随点C的运动而变化,最大值为
B、随点C的运动而变化,最大值为8
C、随点C的运动而变化,最大值为 D、随点C的运动而变化,但无最值
6. 设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )A、有最大值 π B、有最小值 π C、有最大值 π D、有最小值 π7. 如图,在扇形中, , 平分交于点D,点C是半径上一动点,若 , 则阴影部分周长的最小值为( )
D、随点C的运动而变化,但无最值
6. 设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积( )A、有最大值 π B、有最小值 π C、有最大值 π D、有最小值 π7. 如图,在扇形中, , 平分交于点D,点C是半径上一动点,若 , 则阴影部分周长的最小值为( )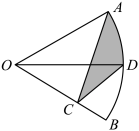 A、 B、 C、 D、8. 如图,是线段上一点,和是位于直线同侧的两个等边三角形,点分别是的中点.若 , 则下列结论错误的是( )
A、 B、 C、 D、8. 如图,是线段上一点,和是位于直线同侧的两个等边三角形,点分别是的中点.若 , 则下列结论错误的是( )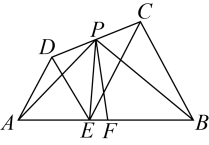 A、的最小值为 B、的最小值为 C、周长的最小值为6 D、四边形面积的最小值为9. 如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A、的最小值为 B、的最小值为 C、周长的最小值为6 D、四边形面积的最小值为9. 如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )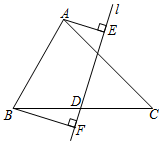 A、 B、2 C、2 D、310. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )
A、 B、2 C、2 D、310. 如图,分别经过原点和点的动直线 , 夹角 , 点是中点,连接 , 则的最大值是( )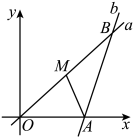 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在平面直角坐标系中 A(3,0),B(0,4),AB=5,P 是线段 AB 上的一个动点,则 OP 的最小值是 .
 12. 如图所示的图案绕中心旋转n°后能与原来的图案完全重合,则n的最小值为
12. 如图所示的图案绕中心旋转n°后能与原来的图案完全重合,则n的最小值为 13. 如图,点C为线段 的中点,E为直线 上方的一点,且满足 ,连接 ,以 为腰,A为直角顶点作等腰 ,连接 ,当 最大,且最大值为 时,则 .
13. 如图,点C为线段 的中点,E为直线 上方的一点,且满足 ,连接 ,以 为腰,A为直角顶点作等腰 ,连接 ,当 最大,且最大值为 时,则 .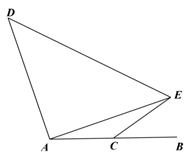 14. 如图,是直径,点C是上一点,且 , 点D是的中点,点P是直径上一动点,则的最小值为 .
14. 如图,是直径,点C是上一点,且 , 点D是的中点,点P是直径上一动点,则的最小值为 .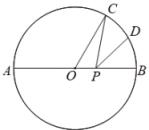 15. 如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=6,则点O到AC距离的最大值为.
15. 如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=6,则点O到AC距离的最大值为.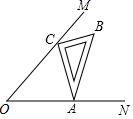 16. 三角形的两条边长分别为4和 , 若第三条边长为整数,则第三条边长的最大值为 .17. 平面直角坐标系中,已知点( , ),且实数 , 满足 , 则点到原点的距离的最小值为.18. 如图,在中, , , 为边上一点,将绕点顺时针旋转得到 , 连接 , 则长度的最小值为.
16. 三角形的两条边长分别为4和 , 若第三条边长为整数,则第三条边长的最大值为 .17. 平面直角坐标系中,已知点( , ),且实数 , 满足 , 则点到原点的距离的最小值为.18. 如图,在中, , , 为边上一点,将绕点顺时针旋转得到 , 连接 , 则长度的最小值为. 19. 如图,抛物线与x轴交于A , B两点,P是以点为圆心,2cm为半径的圆上的动点,Q是线段PA的中点,连接OQ , 则线段OQ的最大值是.
19. 如图,抛物线与x轴交于A , B两点,P是以点为圆心,2cm为半径的圆上的动点,Q是线段PA的中点,连接OQ , 则线段OQ的最大值是.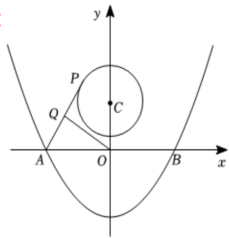 20. 已知线段 , 、为直线上任意两点,将线段、分别沿着点和折叠,使得的对应点为 , 的对应点为 , 若 , 则的最大值和最小值的差为.
20. 已知线段 , 、为直线上任意两点,将线段、分别沿着点和折叠,使得的对应点为 , 的对应点为 , 若 , 则的最大值和最小值的差为. 21. 在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为 .
21. 在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为 . 22. 如图,在矩形中, , 对角线、相交于点O , . 点E是的中点,若点F是对角线上一点,则的最小值是 .
22. 如图,在矩形中, , 对角线、相交于点O , . 点E是的中点,若点F是对角线上一点,则的最小值是 .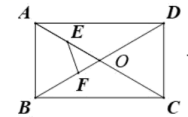 23. 等腰直角中, , , 点D是平面内一点, , 连接 , 将绕D点逆时针旋转90°得到 , 连接 , 当(填度数)度时,可以取最大值,最大值等于 .
23. 等腰直角中, , , 点D是平面内一点, , 连接 , 将绕D点逆时针旋转90°得到 , 连接 , 当(填度数)度时,可以取最大值,最大值等于 .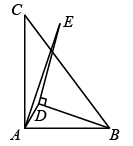
三、综合题
-
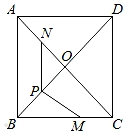
24. 在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6,P为对角线BD上一个动点,求PM﹣PN的最大值.
 25. 如图
25. 如图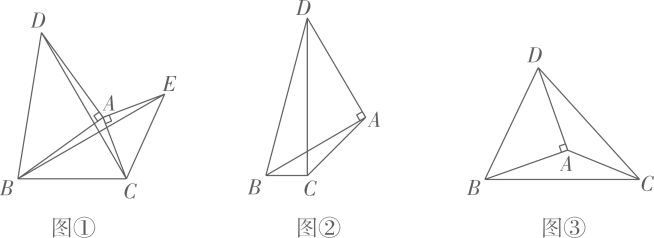
[感知]如图①,以△ABC的边AB、AC为直角边,A为直角顶点,向外作等腰直角△ABD和等腰直角△ACE,连结BE、CD,易知△ADC≌△ABE.(不要求证明)
[探究]如图②,在△ABC中,已知∠ACB=135°,∠BAD=90°,BC=1,AC=2,AB=AD,求CD的长.
[应用]如图③,在△ABC中,BC=2,AC=1.以△ABC的边AB为直角边,A为直角顶点,向外作等腰直角△ABD,则线段CD长度的最大值是 ▲
26. 对于平面直角坐标系xOy中的图形M和点P给出如下定义:Q为图形M上任意一点,若P,Q两点间距离的最大值和最小值都存在,且最大值是最小值的2倍,则称点P为图形M的“二分点”.已知点N(3,0),A(1,0), , .
 (1)、①在点A,B,C中,线段ON的“二分点”是 ;
(1)、①在点A,B,C中,线段ON的“二分点”是 ;②点D(a,0),若点C为线段OD的“二分点”,求a的取值范围;
(2)、以点O为圆心,r为半径画圆,若线段AN上存在的“二分点”,直接写出r的取值范围.27. 对于平面直角坐标系中的两个图形K1和K2 , 给出如下定义:点G为图形K1上任意一点,点H为K2图形上任意一点,如果G,H两点间的距离有最小值,则称这个最小值为图形K1和K2的“近距离”。如图1,已知△ABC,A(-1,-8),B(9,2),C(-1,2),边长为的正方形PQMN,对角线NQ平行于x轴或落在x轴上.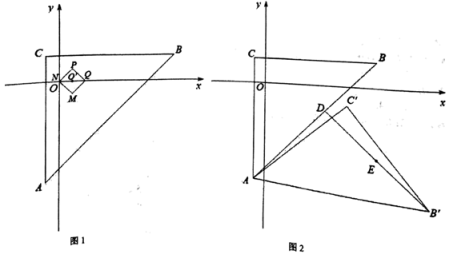 (1)、填空:
(1)、填空:①原点O与线段BC的“近距离”为;
②如图1,正方形PQMN在△ABC内,中心O’坐标为(m,0),若正方形PQMN与△ABC的边界的“近距离”为1,则m的取值范围为;
(2)、已知抛物线C: , 且-1≤x≤9,若抛物线C与△ABC的“近距离”为1,求a的值;(3)、如图2,已知点D为线段AB上一点,且D(5,-2),将△ABC绕点A顺时针旋转α(0°<α≤180°),将旋转中的△ABC记为△AB’C’,连接DB’,点E为DB’的中点,当正方形PQMN中心O’坐标为(5,-6),直接写出在整个旋转过程中点E运动形成的图形与正方形PQMN的“近距离”.28. 在平面直角坐标系中,给出如下定义:若点在图形上,点在图形上,如果两点间的距离有最小值,那么称这个最小值为图形的“近距离”,记为 . 特别地,当图形与图形有公共点时, .已知A(-4,0),B(0,4),C(4,0),D(0,-4),
(1)、d(点A,点C)= , d(点A,线段BD)=;(2)、⊙O半径为r,① 当r = 1时,求 ⊙O与正方形ABCD的“近距离”d(⊙O,正方形ABCD);
② 若d(⊙O,正方形ABCD)=1,则r = ▲ .
(3)、M 为x轴上一点,⊙M的半径为1,⊙M与正方形ABCD的“近距离”d(⊙M,正方形ABCD)<1,请直接写出圆心M的横坐标 m的取值范围.29. 在平面直角坐标系中, 是第一象限内一点,给出如下定义: 和 两个值中的最大值叫做点P的“倾斜系数”k.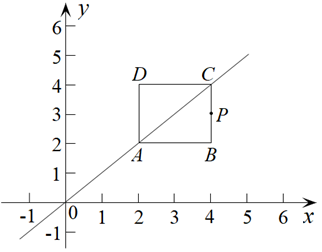 (1)、求点 的“倾斜系数”k的值;(2)、①若点 的“倾斜系数” ,请写出a和b的数量关系,并说明理由;
(1)、求点 的“倾斜系数”k的值;(2)、①若点 的“倾斜系数” ,请写出a和b的数量关系,并说明理由;②若点 的“倾斜系数” ,且 ,求OP的长;
(3)、如图,边长为2的正方形ABCD沿直线AC: 运动, 是正方形ABCD上任意一点,且点P的“倾斜系数” ,请直接写出a的取值范围.30. 对于平面内的点P和图形M , 给出如下定义:以点P为圆心,r为半径作圆,若 与图形M有交点,且半径r存在最大值与最小值,则将半径r的最大值与最小值的差称为点P视角下图形M的“宽度 ”.(1)、如图1.点 , . ①在点O视角下,则线段 的“宽度 ”为;
①在点O视角下,则线段 的“宽度 ”为;②若 半径为1.5,在点A视角下, 的“宽度 ”为;
(2)、如图2, 半径为2,点P为直线 上一点.求点P视角下 “宽度 ”的取值范围;(3)、已知点 ,直线 与x轴,y轴分别交于点D , E .若随着点C位置的变化,使得在所有点K的视角下,线段 的“宽度”均满足 ,直接写出m的取值范围.
31. 阅读下列材料,完成相应的任务数学活动课上,老师提出如下问题:
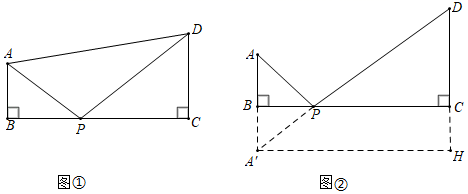
如图①,在四边形ABCD中,AB⊥BC,DC⊥BC,AB=2,DC=4,BC=8,点P为BC边上的动点,求当BP的值是多少时,AP+DP有最小值,最小值是多少.
小丽和小明对老师提出的问题进行了合作探究:
小丽:设BP=x,则CP=8﹣x,根据勾股定理,可得AP+DP= .但没有办法继续求解.
小明:利用轴对称作图,如图②,作点A关于直线BC的对称点A′,连接A′D,与BC交于点P,根据两点之间线段最短,将求AP+DP的最小值转化为求线段A'D的长.
由△A′BP∽△DCP,得 = =
所以BP= .
过点A′作A′H⊥DC,交DC的延长线于点H,再由勾股定理,可得A′D= = =10.
所以当BP= 时,AP+DP有最小值,最小值为10.
任务:
(1)、类比探究:对于函数y= ,当x=时,y有最小值,最小值为.(2)、应用拓展:如图③,若点D在BC上运动,AD⊥BC,AD=3,BC=5.连接AB,AC.求△ABC周长的最小值.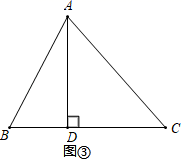 32. (概念学习)
32. (概念学习)在平面直角坐标系 中, 的半径为 ,若 平移 个单位后,使某图形上所有点在 内或 上,则称 的最小值为 对该图形的“最近覆盖距离”.例如,如图①, ,则 对线段 的“最近覆盖距离”为 .

(概念理解)
(1)、 对点 的“最近覆盖距离”为_.(2)、如图②,点 是函数 图象上一点,且 对点 的“最近覆盖距离”为 ,则点 的坐标为_.(3)、如图③,若一次函数 的图象上存在点 ,使 对点 的“最近覆盖距离”为 ,求 的取值范围.(4)、 ,且 ,将 对线段 的“最近覆盖距离”记为 ,则 的取值范围是.33. 【定义】在平面内,把一个图形上任意一点与另一个图形上任意一点之间的距离的最小值,称为这两个图形之间的距离,即A,B分别是图形M和图形N上任意一点,当的长最小时,称这个最小值为图形M与图形N之间的距离.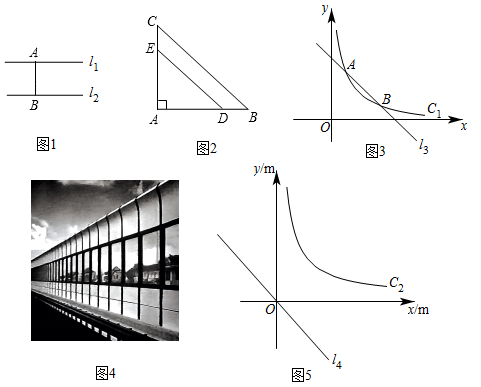
例如,如图1, , 线段的长度称为点A与直线之间的距离,当时,线段的长度也是与之间的距离.
(1)、【应用】
如图2,在等腰中, , , 点D为边上一点,过点D作交于点E.若 , , 则与之间的距离是;(2)、如图3,已知直线与双曲线交于与B两点,点A与点B之间的距离是 , 点O与双曲线之间的距离是;(3)、【拓展】
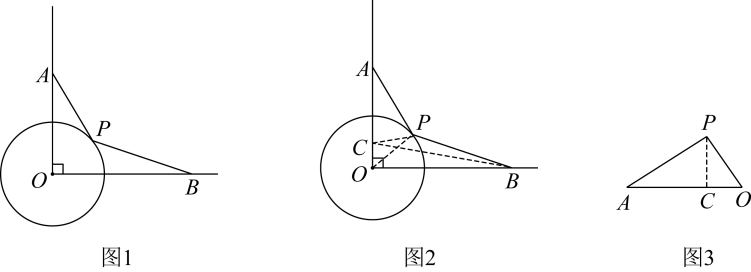
按规定,住宅小区的外延到高速路的距离不超过时,需要在高速路旁修建与高速路相同走向的隔音屏障(如图4).有一条“东南−西北”走向的笔直高速路,路旁某住宅小区建筑外延呈双曲线的形状,它们之间的距离小于.现以高速路上某一合适位置为坐标原点,建立如图5所示的直角坐标系,此时高速路所在直线的函数表达式为 , 小区外延所在双曲线的函数表达式为 , 那么需要在高速路旁修建隔音屏障的长度是多少?34.【问题呈现】如图1,∠AOB=90°, OA=4,OB=5,点P在半径为2的⊙O上,求的最小值.
【问题解决】小明是这样做的:如图2,在OA上取一点C使得OC=1,这样可得 , 又因为∠COP=∠POA,所以可得△COP ∽△POA,所以 , 得所以.
又因为 , 所以最小值为 ▲ .
【思路点拨】小明通过构造相似形(图3),将转化成CP,再利用“两点之间线段”最短”求出CP+ BP的最小值.
【尝试应用】如图4,∠AOB=60°, OA=10,OB=9,点P是半径为6的⊙O上一动点,求的最小值.
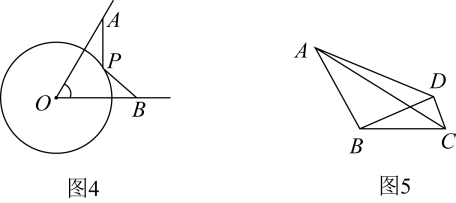
【能力提升】如图5,∠ABC=120°, BA= BC=8,点D为平面内一点且BD= 3CD,连接AD,则△ABD面积的最大值为 ▲ .
 35. (实际问题)小明家住 楼.一天,他要把一根 米长的竹竿放入电梯带回家中,如果竹竿恰好刚能放入电梯中(如图①示)那么,电梯的长、宽、高和的最大值是多少米?
35. (实际问题)小明家住 楼.一天,他要把一根 米长的竹竿放入电梯带回家中,如果竹竿恰好刚能放入电梯中(如图①示)那么,电梯的长、宽、高和的最大值是多少米?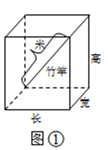
(类比探究)为了解决这个实际问题,我们首先探究下面的数学问题.
探究:如图②,在 中, .若 , , ,则 与 之有什么数量关系?
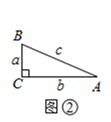
解:在 中,
,
,即 .
,
,
,
,
.
.
, , 均大于 ,
与 之间的数量关系是 .
(1)、探究2:如图③,在四边形 中, 是对角线, , .若 , , , ,则 与 之间有什么数量关系?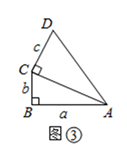
解: , ,
, .
, , ,
, , .
将上面三式相加得, ,
.
.
.
, , , 均大于 ,
与 之间有这样的数量关系: .
(2)、探究3:如图④,仿照上面的方法探究,在五边形 中, , 是对角线, , , .若 , , , , ,则 与 之间的数量关系是 .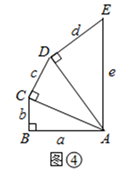 (3)、当 , ,…, , 时,若 ,则 与 之间的数量关系是 .(4)、小明家住 楼一天,他要把一根 米长的竹竿放入电梯带回家中,如果竹竿恰好刚能放入电梯中(如图①示),那么,电梯的长、宽、高和的最大值是米.(5)、公园准备修建一个四边形水池,边长分别为 米, 米, 米, 米,分别以水池四边为边向外建四个正方形花园,若花园面积和为 平方米,则水池的最大周长为米.
(3)、当 , ,…, , 时,若 ,则 与 之间的数量关系是 .(4)、小明家住 楼一天,他要把一根 米长的竹竿放入电梯带回家中,如果竹竿恰好刚能放入电梯中(如图①示),那么,电梯的长、宽、高和的最大值是米.(5)、公园准备修建一个四边形水池,边长分别为 米, 米, 米, 米,分别以水池四边为边向外建四个正方形花园,若花园面积和为 平方米,则水池的最大周长为米.