备考2024年中考数学核心素养专题十一数与式的最值问题

试卷更新日期：2024-03-10 类型：二轮复习

进入出卷网下载

一、选择题

1. 已知正整数a，b，c满足2a=b+270，a+7c=6b，则a的最小值为（）

A、141 B、153 C、160 D、174

查看试题解析
2. 已知实数m，n满足 $m^{2} + n^{2} = 2 + m n$ ，则 ${(2 m - 3 n)}^{2} + (m + 2 n) (m - 2 n)$ 的最大值为（）

A、24 B、 $\frac{44}{3}$ C、 $\frac{16}{3}$ D、-4

查看试题解析
3. 代数式 $\sqrt{x - 1} + \sqrt{x - 2} + \sqrt{x + 2}$ 的最小值是（）

A、0 B、3 C、 $\sqrt{3}$ D、不存在

查看试题解析
4. 设 $x$ 是有理数， $y = | x - 1 | + | x + 1 |$ ，则正确的是（）

A、没有最小值 B、只有一个 $x$ 使 $y$ 取到最小值 C、有有限多个 $x$ （不止一个）使 $y$ 取到最小值 D、有无穷多个 $x$ 使 $y$ 取到最小值

查看试题解析
5. 求 $| \frac{1}{2} x - 1 | + | \frac{1}{3} x - 2 | + | \frac{1}{4} x - 3 |$ 的最小值（　　）

A、12 B、6 C、 $\frac{7}{2}$ D、3

查看试题解析
6. 定义：关于x的一元二次方程： $a_{1} (x - m)^{2} + n = 0$ 与 $a_{2} (x - m)^{2} + n = 0$ ，称为“同族二次方程”．如2（x﹣3）²+4＝0与3（x﹣3）²+4＝0是“同族二次方程”．若关于x的一元二次方程：2（x﹣1）²+1＝0与（a+2）x²+（b﹣4）x+8＝0是“同族二次方程”．则代数式﹣ax²+bx+2019的最大值是（　　）

A、2024 B、2023 C、2022 D、2021

查看试题解析
7. 定义平面内任意两点P(x₁ ， y₁)、Q(x₂ ， y₂)之间的距离d_PQ=|x₂-x₁|+|y₂-y₁|称为这两点间的曼哈顿距离(简称为曼距)．例如，在平面直角坐标系中，点P(-3，-2)与点Q(2，2)之间的曼距d_PQ=|-3-2|+|-2-2|=5+4=9，若点A在直线y= $\frac{1}{2}$ x-2上，点B为抛物线y=x²+2x上一点，则曼距d_AB的最小值（）

A、 $\frac{23 \sqrt{5}}{40}$ B、 $\frac{69}{40}$ C、 $\frac{23}{16}$ D、 $\frac{3}{2}$

查看试题解析
8. 已知点 $P (m ， n)$ 在直线 $y = - x + 4$ 上，且 $2 m - 5 n \geq 0$ ，则（）

A、 $\frac{n}{m}$ 有最大值 $\frac{2}{5}$ B、 $\frac{n}{m}$ 有最小值 $\frac{2}{5}$ C、 $\frac{m}{n}$ 有最大值 $\frac{5}{2}$ D、 $\frac{m}{n}$ 有最小值 $\frac{5}{2}$

查看试题解析
9. 关于二次函数 $y = 2 {(x - 4)}^{2} + 6$ 的最大值或最小值，下列说法正确的是（）

A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6

查看试题解析
10. 在平面直角坐标系xOy中，若点P的横坐标和纵坐标相等，则称点P为雅系点．已知二次函数 $y = a x^{2} - 4 x + c (a \neq 0)$ 的图象上有且只有一个雅系点 $(- \frac{5}{2} ， - \frac{5}{2})$ ，且当 $m \leq x \leq 0$ 时，函数 $y = a x^{2} - 4 x + c + \frac{1}{4} (a \neq 0)$ 的最小值为 $- 6$ ，最大值为 $- 2$ ，则m的取值范围是（）

A、 $- 1 \leq m \leq 0$ B、 $- \frac{7}{2} < m \leq - 2$ C、 $- 4 \leq m \leq - 2$ D、 $- \frac{7}{2} \leq m < - \frac{9}{4}$

查看试题解析
11. 对于实数a、b ，定义新运算 $a * b = {\begin{cases} a^{2} - a b (a \geq b) \\ b^{2} - a b (a < b) \end{cases}$ ，若二次函数 $y = 2 x * (x - 1)$ ，则下列结论正确的有（）
①方程 $2 x * (x - 1) = 0$ 的解为x = 0 或x= − 1； ②关于x的方程 $2 x * (x - 1) = m$ 有三个解，则 $0 \leq m < \frac{1}{2}$ ； ③当x<− 1 时，y随x增大而增大； ④当x > − 1 时，函数 $y = 2 x * (x - 1)$ 有最大值 0．

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析

二、填空题

12. 嘉淇准备完成题目：解一元二次方程 $x^{2} - 6 x +$ □ $= 0$ .若“□”表示一个数字，且一元二次方程 $x^{2} - 6 x +$ □ $= 0$ 有实数根，则“□”的最大值为；此时方程的解为.

查看试题解析
13. 已知m为正整数，若 $\sqrt{189 m}$ 是整数，则根据 $\sqrt{189 m} = \sqrt{3 \times 3 \times 3 \times 7 m} = 3 \sqrt{3 \times 7 m}$ 可知m有最小值 $3 \times 7 = 21$ .设n为正整数，若 $\sqrt{\frac{300}{n}}$ 是大于1的整数，则n的最小值为，最大值为.

查看试题解析
14. 已知x，y，z为实数，满足 ${\begin{array}{l} x + 2 y - z = 6 \\ x - y + 2 z = 3 \end{array}$ ，那么x²+y²+z²的最小值是

查看试题解析
15. 已知函数y $= {\begin{array}{l} 12 （ 1 \leq x ＜ 3 ） \\ （ x - 5 ）^{2} + 8 （ 3 \leq x \leq 8 ） \end{array}$ 的图象如图所示，若直线y＝kx﹣3与该图象有公共点，则k的最大值与最小值的和为．

查看试题解析
16. 已知点P（m，n）在双曲线上 $y = \frac{1}{x}$ ，则m²-3mn+n²的最小值为．

查看试题解析
17. 由直线 $y = k x + 2 k - 1$ 和直线 $y = (k + 1) x + 2 k + 1 (k$ 是正整数 $)$ 与 $x$ 轴及 $y$ 轴所围成的图形面积为 $S$ ，则 $S$ 的最小值是．

查看试题解析
18. 若一个四位正整数 $a b c d$ 满足：a+c＝b+d ，我们就称该数是“交替数”，则最小的“交替数”是；若一个“交替数”m满足千位数字与百位数字的平方差是15，且十位数字与个位数的和能被5整除．则满足条件的“交替数”m的最大值为．

查看试题解析

三、综合题

19. 已知非负数 $a ， b ， c$ ，且有 $a + b = 2 ， c - 3 a = 4$ ．设 $S = a^{2} + b + c$ ，记 $S$ 的最大值为 $m ， S$ 的最小值为 $n$ ，求 $m$ 和 $n$ 的值．

查看试题解析
20. 阅读下面的材料：
我们可以用配方法求一个二次三项式的最大值或最小值，例如：求代数式 $a^{2} - 2 a + 5$ 的最小值.方法如下：

∵ $a^{2} - 2 a + 5 = a^{2} - 2 a + 1 + 4 = {(a - 1)}^{2} + 4$ ，由 ${(a - 1)}^{2} \geq 0$ ，得 ${(a - 1)}^{2} + 4 \geq 4$ ；

∴代数式 $a^{2} - 2 a + 5$ 的最小值是4.

(1)、仿照上述方法求代数式 $x^{2} + 10 x + 7$ 的最小值.

(2)、代数式 $- a^{2} - 8 a + 16$ 有最大值还是最小值？请用配方法求出这个最值.

查看试题解析
21. 我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用．
例：已知x可取任何实数，试求二次三项式 $x^{2} + 6 x - 1$ 最小值．
解： $x^{2} + 6 x - 1 = x^{2} + 2 \times 3 · x + 3^{2} - 3^{2} - 1$
$= {(x + 3)}^{2} - 10$
∵无论x取何实数，总有 ${(x + 3)}^{2} \geq 0$ ．
∴ ${(x + 3)}^{2} - 10 \geq - 10$ ，即 $x^{2} + 6 x - 1$ 的最小值是 $- 10$ ．
即无论x取何实数， $x^{2} + 6 x - 1$ 的值总是不小于 $- 10$ 的实数．
问题：

(1)、已知 $y = x^{2} - 4 x + 7$ ，求证y是正数；

(2)、知识迁移：如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 6 c m$ ， $B C = 4 c m$ ，点P在边 $A C$ 上，从点A向点C以 $2 c m / s$ 的速度移动，点Q在 $C B$ 边上以 $\sqrt{3} c m / s$ 的速度从点C向点B移动若点P，Q同时出发，且当一点移动到终点时，另一点也随之停止，设 $△ P C Q$ 的面积为 $S c m^{2}$ ，运动时间为t秒时S最大，请求出t和S的值，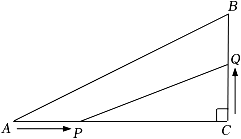

查看试题解析
22. 【阅读理解】我们知道 $a^{2} \geq 0$ ，所以代数式 $a^{2}$ 的最小值为0，可以用公式 $a^{2} \pm 2 a b + b^{2} = {(a \pm b)}^{2}$ 来求一些多项式的最小值.
例如：求 $x^{2} + 6 x + 1$ 的最小值问题.
解：∵ $x^{2} + 6 x + 1 = x^{2} + 6 x + 9 - 9 + 1 = {(x + 3)}^{2} - 8$ ，
∵ ${(x + 3)}^{2} \geq 0$ ， ∴ ${(x + 3)}^{2} - 8 \geq - 8$ ，
∴ $x^{2} + 6 x + 1$ 的最小值为－8.
【类比应用】请应用上述思想方法，解决下列问题：

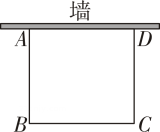(1)、类比： $x^{2} + 4 x + 6$ 的最小值为.

(2)、探究：代数式 $- x^{2} + 2 x$ 有最（填“大”或“小”）值，为.

(3)、拓展：如图，长方形花圃一面靠墙（墙足够长）另外三面所围成的棚栏的总长是20米，设垂直墙面的棚栏围x米，则当x为多长时花圃面积最大，最大面积是多少？

查看试题解析
23. 对于“已知 $x + y = 1$ ，求 $x y$ 的最大值”这个问题，小明是这样求解的：
∵ $x + y = 1$ ， ∴ $y = 1 - x$ ， ∴ $x y = x (1 - x) = x - x^{2} = - {(x - \frac{1}{2})}^{2} + \frac{1}{4}$
∴ $x y \leq \frac{1}{4}$ ，所以 $x y$ 的最大值为 $\frac{1}{4}$ .
请你按照这种方法计算：当 $2 n + m = 4 (m > 0 ， n > 0)$ 时， $\frac{2}{m} + \frac{1}{n}$ 的最小值.

查看试题解析
24. 在 $y$ 关于 $x$ 的函数中，对于实数 $a$ ， $b$ ，当 $a \leq x \leq b$ 且 $b = a + 3$ 时，函数 $y$ 有最大值 $y_{m a x}$ ，最小值 $y_{m i n}$ ，设 $h = y_{m a x} - y_{m i n}$ ，则称 $h$ 为 $y$ 的“极差函数” $($ 此函数为 $h$ 关于 $a$ 的函数 $)$ ；特别的，当 $h = y_{m a x} - y_{m i n}$ 为一个常数 $($ 与 $a$ 无关 $)$ 时，称 $y$ 有“极差常函数”．

(1)、判断下列函数是否有“极差常函数”？如果是，请在对应内画“ $\sqrt$ ”，如果不是，请在对应内画“ $\times$ ”．（）
$① y = 2 x$ （）；

$② y = - 2 x + 2$ （）；

$③ y = x^{2}$ （）

(2)、y关于 $x$ 的一次函数 $y = p x + q$ ，它与两坐标轴围成的面积为1，且它有“极差常函数” $h = 3$ ，求一次函数解析式；

(3)、若 $\frac{- 1 + \sqrt{13}}{2} \leq a \leq \frac{3}{2}$ ，当 $a \leq x \leq b (b = a + 3)$ 时，写出函数 $y = a x^{2} - b x + 4$ 的“极差函数” $h$ ；并求 $4 a h$ 的取值范围．

查看试题解析
25. 在平面直角坐标系xOy中，图形W上任意两点间的距离有最大值，将这个最大值记为d．对点P及图形W给出如下定义：点Q为图形W上任意一点，若P，Q两点间的距离有最大值，且最大值恰好为2d，则称点P为图形W的“倍点”．

(1)、如图1，图形W是半径为1的⊙O．
①图形W上任意两点间的距离的最大值d为；
②在点 $P_{1}$ （0，2）， $P_{2}$ （3，3）， $P_{3}$ （ $- 3$ ， 0）中，⊙O的“倍点”是；

(2)、如图2，图形W是中心在原点的正方形ABCD，已知点A（-1，1），若点E（t，3）是正方形ABCD的“倍点”，求t的值；

(3)、图形W是长为2的线段MN，T为MN的中点，若在半径为6的⊙O上存在MN的“倍点”，直接写出满足条件的点T所构成的图形的面积．

查看试题解析
26. 若关于x的函数y，当 $t - \frac{1}{2} \leq x \leq t + \frac{1}{2}$ 时，函数y的最大值为M，最小值为N，令函数 $h = \frac{M - N}{2}$ ，我们不妨把函数h称之为函数y的“共同体函数”.

(1)、①若函数 $y = 4044 x$ ，当 $t = 1$ 时，求函数y的“共同体函数”h的值；
②若函数 $y = k x + b$ （ $k \neq 0$ ， k，b为常数），求函数y的“共同体函数”h的解析式；

(2)、若函数 $y = \frac{2}{x} （ x \geq 1 ）$ ，求函数y的“共同体函数”h的最大值；

(3)、若函数 $y = - x^{2} + 4 x + k$ ，是否存在实数k，使得函数y的最大值等于函数y的“共同体函数”h的最小值.若存在，求出k的值；若不存在，请说明理由.

查看试题解析
27. 对于平面直角坐标系 $x O y$ 中的点P和图形M ，给出如下定义：Q为图形M上任意一点，如果 $P ， Q$ 两点间的距离有最大值，那么称这个最大值为点P与图形M间的开距离，记作 $d (P ， M)$ ．已知直线 $y = \frac{\sqrt{3}}{3} x + b (b \neq 0)$ 与x轴交于点A ，与y轴交于点B ， $⊙ O$ 的半径为1．

(1)、若 $b = 2$ ，
①求 $d (B ， ⊙ O)$ 的值；

②若点C在直线 $A B$ 上，求 $d (C ， ⊙ O)$ 的最小值；

(2)、以点A为中心，将线段 $A B$ 顺时针旋转 $120^{°}$ 得到 $A D$ ，点E在线段 $A B ， A D$ 组成的图形上，若对于任意点E ，总有 $2 ⩽ d (E ， ⊙ O) < 6$ ，直接写出b的取值范围．

查看试题解析
28. 若二次函数y₁＝ax²＋4x＋b与y₂＝bx²＋4x＋a均有最小值，记y₁ ， y₂的最小值分别为m ， n ．

(1)、若a＝4，b＝1，求m ， n的值．

(2)、若m＋n＝0，求证：对任意的实数x ，都有y₁＋y₂≥0．

(3)、若m ， n均大于0，且mn＝2，记M为m ， n中的较大者，求M的最小值．

查看试题解析

备考2024年中考数学核心素养专题十一 数与式的最值问题

一、选择题

二、填空题

三、综合题

备考2024年中考数学核心素养专题十一数与式的最值问题