备考2024年中考数学核心素养专题九数与式的探究型问题

试卷更新日期：2024-03-10 类型：二轮复习

进入出卷网下载

一、选择题

1. 我们这样来探究二次根式 $\sqrt{a^{2}}$ 的结果，当a＞0时，如a=3，则 $\sqrt{3^{2}}$ =3，此时 $\sqrt{a^{2}}$ 的结果是a本身；当a=0时， $\sqrt{0^{2}}$ =0．此时 $\sqrt{a^{2}}$ 的结果是零；当a＜0时，如a=﹣3，则 $\sqrt{{(- 3)}^{2}}$ =﹣（﹣3）=3，此时 $\sqrt{a^{2}}$ 的结果是a的相反数．这种分析问题的方法所体现的数学思想是（）

A、分类讨论 B、数形结合 C、公理化 D、转化

查看试题解析
2. 观察下列关于 $a$ 的单项式，探究其规律： $a$ ， $3 a^{2}$ ， $5 a^{3}$ ， $7 a^{4}$ ， $9 a^{5}$ ， …按照上述规律，第2023个单项式是（）

A、 $2023 a^{2023}$ B、 $4046 a^{2023}$ C、 $4045 a^{2023}$ D、 $4047 a^{2023}$

查看试题解析
3. 观察下列两行数：
0，2，4，6，8，10，12，14，16，…
0，3，6，9，12，15，18，21，24，…
探究发现：第1个相同的数是0，第2个相同的数是6，…，若第n个相同的数是102，则n等于（）

A、18 B、19 C、20 D、21

查看试题解析
4. 小华仿照探究一元二次方程解的方法，课后尝试探究了一元三次方程 $x^{3} + 12 x - 15 x - 1 = 0$ 的解，列表如下：
x
0
0.5
1
1.5
2
$x^{3} + 12 x - 15 x - 1$
－1
－5.375
－3
6.875
25
据此可知，方程 $x^{3} + 12 x - 15 x - 1 = 0$ 的一个解x的取值范围是（）

A、 $0 < x < 0.5$ B、 $0.5 < x < 1$ C、 $1 < x < 1.5$ D、 $1.5 < x < 2$

查看试题解析
5. 某数学小组在研究了函数y₁=x与y₂＝ $\frac{4}{x}$ 性质的基础上，进一步探究函数y=y₁＋y₂的性质，经过讨论得到以下几个结论：①函数y=y₁＋y₂的图象与直线y=3没有交点；②函数y=y₁＋y₂的图象与直线y=a只有一个交点，则a=±4；③点（a，b）在函数y=y₁＋y₂的图象上，则点（－a，－b）也在函数y=y₁＋y₂的图象上．以上结论正确的是（）

A、①② B、①②③ C、②③ D、①③

查看试题解析
6. 学习完函数的有关知识之后，强强对函数产生了浓厚的兴趣，他利用绘图软件画出函数 $y = \frac{1}{x + 2}$ 的图象并对该函数的性质进行了探究．下面推断正确的是（   ）

①该函数的定义域为 $x \neq - 2$ ；

②该函数与x轴没有交点；

③该函数与y轴交于点 $(0 ， \frac{1}{2})$ ；

④若 $(x_{1} ， y_{1}) ， (x_{2} ， y_{2})$ 是该函数上两点，当 $x_{1} < x_{2}$ 时，一定有 $y_{1} > y_{2}$ .

A、①②③④ B、①③ C、① ②③ D、②③④

查看试题解析
7. 在数学活动课上，王老师出示一道数学题目：“在平面直角坐标系 $x o y$ 中，当 $c$ 为何值时，抛物线 $L ： y = - x (x - 4) + c$ 与直线段 $l ： y = x + 3 (0 \leq x \leq 4)$ 有唯一公共点或有两个公共点？”某学习小组经探究得到以下四个结论：
①当 $c = \frac{3}{4}$ 时，有唯一公共点；②若 $c$ 为整数，则仅当 $c$ 的值为4或5或6或7时，才有唯一公共点；③若 $c$ 为整数，则当 $c$ 的值为1或2或3时，有两个公共点；④当 $3 < c < 7$ 时，有两个公共点．其中正确的结论有（）

A、①②④ B、①②③ C、①③ D、①④

查看试题解析
8. 小明、小亮、小梅、小花四人共同探究代数式x²-4x+5的值的情况，他们作了如下分工：小明负责找值为1时的x值，小亮负责找值为0时的x值，小梅负责找最小值，小花负责找最大值。几分钟后，各自通报探究的结论，其中错误的是（）

A、小明认为只有当x=2时，x²-4x+5的值为1； B、小亮认为找不到实数x，使x²-4x+5的值为0； C、小花发现当取大于2的实数时，x²-4x+5的值随x的增大而增大，因此认为没有最大值； D、小梅发现x²-4x+5的值随x的变化而变化，因此认为没有最小值；

查看试题解析
9. 观察下列关于x的单项式，探究其规律： $3 x$ ， $\frac{5}{2} x^{2}$ ， $\frac{7}{3} x^{3}$ ， $\frac{9}{4} x^{4}$ ， $\frac{11}{5} x^{5}$ ， $\frac{13}{6} x^{6}$ ， ……，按照上述规律，第2023个单项式是（）

A、 $\frac{4046}{2023} x^{2023}$ B、 $\frac{4047}{2023} x^{2023}$ C、 $\frac{4047}{2022} x^{2022}$ D、 $\frac{4045}{2024} x^{2024}$

查看试题解析
10. 小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 $y = k_{n} x + b_{n} (n = 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7)$ ，其中 $k_{1} = k_{2} ， b_{3} = b_{4} = b_{5}$ ，则他探究这7条直线的交点个数最多是（）

A、17个 B、18个 C、19个 D、21个

查看试题解析

二、填空题

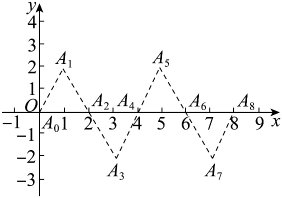
11. 如图，点 $A_{0} (0 ， 0)$ ， $A_{1} (1 ， 2)$ ， $A_{2} (2 ， 0)$ ， $A_{3} (3 ， - 2)$ ， $A_{4} (4 ， 0)$ ……．根据这个规律，探究可得点 $A_{2023}$ 的坐标是．

查看试题解析
12. 在探究一元二次方程x²+12x﹣15＝0的近似解时，小明所在的小组采用了赋值法，计算结果如表：

　x

1.1

1.2

1.3

1.4

x²+12x﹣15

-0.59

0.84

2.29

3.76

小组同学说，他们发现了该方程的一个近似解．这个近似解的十分位是．

查看试题解析
13. 如图，已知 $A$ ， $B$ ， $C$ 是函数 $y = x^{2}$ 图象上的动点，且三点的横坐标依次为 $a + 1$ ， $a$ ， $a - 1 .$ 小华用软件 $G e o G e b r a$ 对 $△ A B C$ 的几何特征进行了探究，发现 $△ A B C$ 的面积是个定值，则这个定值为．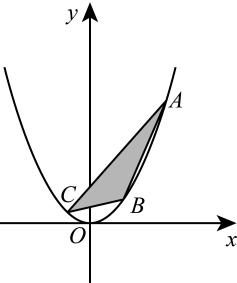

查看试题解析
14. 如图，在平面直角坐标系xOy中，已知抛物线 y=-x(x-3)(0≤x≤3) 在x轴上方部分记作C₁ ，它与x轴交于点O，A₁ ，将C₁绕点A₁旋转180°得C₂ ， C₂与x 轴交于另一点A₂ ．继续操作并探究：将C₂绕点A₂旋转180°得C₃ ，与x 轴交于另一点A₃；将C₃绕点A ₂旋转180°得C₄ ，与x 轴交于另一点A₄ ，这样依次得到x轴上的点A₁ ， A₂ ， A₃ ， …，A_n ， …，及抛物线C₁ ， C₂ ， …，C_n ， …．则点A₄的坐标为；C_n的顶点坐标为(n为正整数，用含n的代数式表示) ．

查看试题解析
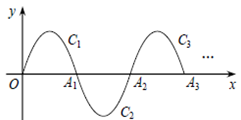15. 在平面直角坐标系xOy中，已知直线l：y＝x ，作A₁（1，0）关于y＝x的对称点B₁ ，将点B₁向右水平平移2个单位得到点A₂；再作A₂关于y＝x的对称点B₂ ，将点B₂向右水平平移2个单位得到点A₃；…．请继续操作并探究：点A₃的坐标是，点B₂₀₁₄的坐标是．

查看试题解析
16. 如图1，点 $A$ 是反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上一点，连接$OA$，过点 $A$ 作 $A A_{I} / / y$ 轴交 $y = \frac{1}{x} (x > 0)$ 的图象于点 $A_{1}$ ，连接 $O A_{1}$ 并延长交 $y = \frac{k}{x} (k > 0)$ 的图象于点 $B$ ，过点 $B$ 作 $B B_{1} / / y$ 轴交 $y = \frac{1}{x} (x > 0)$ 的图象于点 $B_{1}$ ，已知点 $A$ 的横坐标为 $1 ， S_{△ A O A_{1}} = 2 S_{△ B A_{1} B_{1}}$ ，连接 $O B_{1}$ ，小明通过对 $△ A O A_{1}$ 和 $△ B O B_{1}$ 的面积与 $k$ 的关系展开探究，发现 $k$ 的值为；如图2，延长 $O B_{1}$ 交 $y = \frac{k}{x} (k > 0)$ 的图象于点 $C$ ，过点 $C$ 作 $C C_{1} / / y$ 轴交 $y = \frac{1}{x} (x > 0)$ 的图象于点 $C_{1}$ ，依此进行下去.记 $S_{△ B A_{1} B_{1}} = S_{1} ， S_{△ C B_{1} C_{1}} = S_{2} ， \dots \dots$ ，则 $S_{2023} =$ .

查看试题解析

三、实践探究题

17. 阅读材料： $a^{2} - 2 a b + 2 b^{2} - 8 b + 16 = 0$ ，求a，b的值．
解：∵ $a^{2} - 2 a b + 2 b^{2} - 8 b + 16 = 0$ ，
∴ $(a^{2} - 2 a b + b^{2}) + (b^{2} - 8 b + 16) = 0$ ，
∴ ${(a - b)}^{2} + {(b - 4)}^{2} = 0$ ，
∴ ${(a - b)}^{2} = 0 ， {(b - 4)}^{2} = 0$ ，
∴ $a = 4 ， b = 4$ ．
根据你的观察，探究下面的问题：

(1)、若 $m^{2} + n^{2} - 4 m + 4 = 0$ ，则m＝， n＝；

(2)、已知 $x^{2} + 2 y^{2} + 10 y + 25 - 2 x y = 0$ ，求 $x y$ 的值．

查看试题解析
18. 阅读材料：若 $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，求 $m$ 、 $n$ 的值．
解：∵ $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0 ， ∴ (m^{2} - 2 m n + n^{2}) + (n^{2} - 8 n + 16) = 0$
∴ $(m - n)^{2} + (n - 4)^{2} = 0 ， ∴ (m - n)^{2} = 0 ， (n - 4)^{2} = 0 ， ∴ n = 4 ， m = 4$ ．
根据你的观察，探究下面的问题：

(1)、已知 $a^{2} + 6 a b + 10 b^{2} + 2 b + 1 = 0$ ，求 $a - b$ 的值；

(2)、已知等腰 $△ A B C$ 的三边长 $a$ 、 $b$ 、 $c$ 都是正整数，且满足 $2 a^{2} + b^{2} - 4 a - 6 b + 11 = 0$ ，求 $△ A B C$ 的周长；

(3)、已知 $x + y = 2 ， x y - z^{2} - 4 z = 5$ ，求 $x y z$ 的值．

查看试题解析
19. 根据学习函数的经验，对函数y＝|x|－1的图象与性质进行探究，请补充完整下面的探究过程：

(1)、下表是y与x的几组对应值．
x
…
－3
－2
－1
0
1
2
3
…
y
…
2
1
0
－1
0
1
m
…
①m＝；
②若A（n ， 8），B（9，8）为该函数图象上不同的两点，则n＝；

(2)、在下面的平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象．
根据函数图象：
①写出该函数图象的两点性质；
②在同一个平面直角坐标系中画出y₁＝ $\frac{1}{2}$ x的图象，并直接写出当y₁＜y时，x的取值范围．

查看试题解析
20. 某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号，他们将其中某些材料摘录如下：对于三个实数 $a$ ， $b$ ， $c$ ，用 $M {a ， b ， c}$ 表示这三个数的平均数，用 $m i n {a ， b ， c}$ 表示这三个数中最小的数，例如： $M {1，2 ， 9} = \frac{1 + 2 + 9}{3} = 4 ， m i n {1，2 ， - 3} = - 3$ ．
请结合上述材料，解决下列问题：

(1)、 $M {2^{2} ， \sqrt{9} ， - 3^{2}} =$ ；

(2)、若 $M {- 2 x ， x^{2} ， 3} = 2$ ，求 $x$ 的值；

(3)、若 $a > 0$ ，且点 $P (M {- 2 ， a - 1，2 a}$ ， $m i n {- 2 ， a - 1，2 a})$ 在反比例函数 $y = \frac{- 2}{x}$ 的图象上，求 $a$ 的值．

查看试题解析
21. 小东同学根据函数的学习经验，对函数y = $| x - 1 |$ + $| x + 3 |$ 进行了探究，

下面是他的探究过程：

(1)、已知x＝－3时 $| x + 3 |$ = 0；x＝1 时 $| x - 1 |$ = 0，化简：
①当x＜－3时，y＝

②当－3≤x≤1时，y＝

③当x＞1时，y＝

(2)、在平面直角坐标系中画出y = $| x - 1 |$ + $| x + 3 |$ 的图像，根据图像，写出该函数的一条性质.

(3)、根据上面的探究解决，下面问题：
已知A(a，0)是x轴上一动点，B(1，0)，C(－3，0)，则AB＋AC的最小值是

查看试题解析
22. 在学习了二次根式后，小明同学发现有的二次根式可以写成另一个二次根式的平方的形式.
比如： $4 - 2 \sqrt{3} = 3 - 2 \sqrt{3} + 1 = {(\sqrt{3})}^{2} - 2 \times \sqrt{3} \times 1 + 1^{2} = {(\sqrt{3} - 1)}^{2}$ .善于动脑的小明继续探究：
当 $a ， b ， m ， n$ 为正整数时，若 $a + \sqrt{3} b = {(\sqrt{3} m + n)}^{2}$ ，则有 $a + \sqrt{2} b = (2 m^{2} + n^{2}) + 2 \sqrt{2} m n$ ，所以 $a = 2 m^{2} + n^{2}$ ， $b = 2 m n$ .
请模仿小明的方法探索并解决下列问题：

(1)、当 $a ， b ， m ， n$ 为正整数时，若 $a + \sqrt{3} b = {(\sqrt{3} m + n)}^{2}$ ，请用含有 $m ， n$ 的式子分别表示 $a ， b$ ，得： $a =$ ， $b =$ ；

(2)、 $13 - 4 \sqrt{3}$

(3)、若 $a + 6 \sqrt{5} = {(m + \sqrt{5} n)}^{2}$ ，且 $a ， m ， n$ 为正整数，求 $a$ 的值.

查看试题解析
23. 综合与探究：随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车进行销售，据了解，2辆 $A$ 型汽车、3辆 $B$ 型汽车的进价共计80万元；3辆 $A$ 型汽车、2辆 $B$ 型汽车的进价共计95万元.

(1)、问 $A ， B$ 两种型号的汽车每辆进价分别为多少万元？

(2)、若该公司计划正好用200万元购进，以上两种型号的新能源汽车（两种型号的汽车均购买），问该公司有几种购买方案，请你设计出来.

(3)、已知该汽车销售公司销售 $1$ 辆 $A$ 型汽车可获利800元，销售 $1$ 辆 $B$ 型汽车可获利5000元，在（2）中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？

查看试题解析
24. 小宇在学习过程中遇到了一个函数 $y = |x| + \frac{1}{x} (x \neq 0)$ ．
下面是小宇对其探究的过程，请补充完整：

(1)、对于函数 $y_{1} = \frac{1}{x}$ ，当 $x < 0$ 时， $y_{1}$ 随 $x$ 的增大而减小，
对于函数 $y_{2} = |x|$ ，当 $x < 0$ 时， $y_{2}$ 随 $x$ 的增大
而结合上述分析，进一步探究发现，对于函数 $y$ ，当 $x < 0$ 时， $y$ 随 $x$ 的增大而；

(2)、当 $x > 0$ 时，对于函数 $y$ 与 $x$ 的几组对应值如下表：

$x$

$\dots$

$\frac{1}{4}$

$\frac{1}{2}$

$1$

$\frac{3}{2}$

$2$

$\frac{5}{2}$

$\dots$

$y$

$\dots$

$\frac{17}{4}$

$\frac{5}{2}$

$2$

$\frac{13}{6}$

$\frac{5}{2}$

$\frac{29}{10}$

$\dots$
在平面直角坐标系 $x O y$ 中，画出当 $x > 0$ 时函数 $y$ 的图象．

(3)、过点 $(0 ， m)$ 作平行于 $x$ 轴的直线 $l$ ，结合 $(1) (2)$ 的分析，解决问题：
若直线 $l$ 与函数 $y = |x| + \frac{1}{x} (x \neq 0)$ 的图象有两个交点，则 $m =$ ．

查看试题解析
25. 【探究函数 $y = x + \frac{1}{x}$ 的图象与性质】

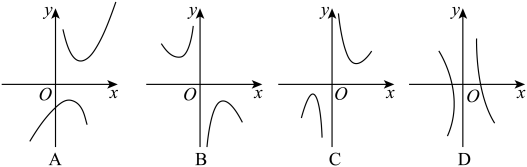(1)、函数 $y = x + \frac{1}{x}$ 的自变量x的取值范围是；

(2)、下列四个函数图象中，函数 $y = x + \frac{1}{x}$ 的图象大致是；

(3)、对于函数 $y = x + \frac{1}{x}$ ，求当 $x > 0$ 时，y的取值范围．请将下列的求解过程补充完整．
解：∵ $x > 0$ ， ∴ $y = x + \frac{1}{x}$ $= {(\sqrt{x})}^{2} + {(\frac{1}{\sqrt{x}})}^{2}$ $= {(\sqrt{x} - \frac{1}{\sqrt{x}})}^{2} +$ ．
∵ ${(\sqrt{x} - \frac{1}{\sqrt{x}})}^{2} \geq 0$ ， ∴ $y \geq$ ．

(4)、【拓展说明】
若函数 $y = \frac{x^{2} - 5 x + 4}{x} (x > 0)$ ，求y的取值范围．

查看试题解析

26. 探究函数

y = - 2 | x |^{2} + 4 | x |

的图象和性质，探究过程如下：

(1)、自变量

x

的取值范围是全体实数，

x

与

y

的几组对应值列表如下：

$x$

$\dots$

$- \frac{5}{2}$

$- 2$

$- \frac{3}{2}$

$- 1$

$- \frac{1}{2}$

$0$

$\frac{1}{2}$

$1$

$\frac{3}{2}$

$2$

$\frac{5}{2}$

$\dots$

$y$

$\dots$

$- \frac{5}{2}$

$0$

$\frac{3}{2}$

$m$

$\frac{3}{2}$

$0$

$\frac{3}{2}$

$2$

$\frac{3}{2}$

$0$

$- \frac{5}{2}$

$\dots$

其中， $m =$ ▲ $.$ 根据如表数据，在图 $1$ 所示的平面直角坐标系中，通过描点画出了函数图象的一部分，请画出该函数图象的另一部分 $.$ 观察图象，写出该函数的一条性质；

(2)、点

F

是函数

y = - 2 | x |^{2} + 4 | x |

图象上的一动点，点

A (2 ， 0)

，点

B (- 2 ， 0)

，当

S_{△ F A B} = 3

时，请直接写出所有满足条件的点

F

的坐标；

(3)、在图

2

中，当

x

在一切实数范围内时，抛物线

y = - 2 x^{2} + 4 x

交

x

轴于

O

，

A

两点

(

点

O

在点

A

的左边

)

，点

P

是点

Q (1 ， 0)

关于抛物线顶点的对称点，不平行

y

轴的直线

l

分别交线段

O P

，

A P (

不含端点

)

于

M

，

N

两点

.

当直线

l

与抛物线只有一个公共点时，

P M

与

P N

的和是否为定值？若是，求出此定值；若不是，请说明理由．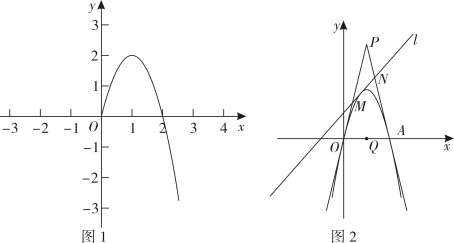

查看试题解析

27. 【问题提出】计算 $1^{2} + 2^{2} + 3^{2} + \cdot \cdot \cdot + n^{2}$ （其中 $n$ 是正整数）
【问题探究】为解决上面的数学问题，我们可以运用数形结合的思想方法，借助图1所示的三角形，把数量关系和几何图形巧妙地结合起来进行探究.图1中，
第1行圆圈中的数为1，即 $1^{2}$ ；
第2行两个圆圈中数的和为2+2=2×2，
即 $2^{2}$ ；
第3行三个圆圈中数的和为3+3+3=3×3
即 $3^{3}$ ；
……；
第 $n$ 行 $n$ 个圆圈中数的和为 $\overset{}{\overset{︷}{n + n + \cdot \cdot \cdot + n}}$ ，即 $n^{2}$ .所有圆圈中数的和为 $1^{2} + 2^{2} + 3^{2} + \cdot \cdot \cdot + n^{2}$ .
要解决上面的问题，我们不妨先从特例入手：
探究一：计算 $1^{2} + 2^{2}$ .
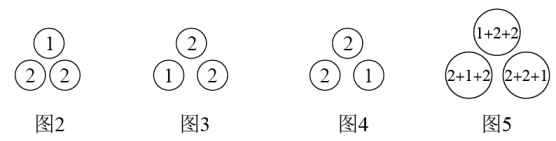
将图2按逆时针方向两次旋转得到图3、图4.观察这三个图形，可以发现同一位置圆圈的数字之和都是5（如图5），而图5共有（1+2）个这样的圆圈，因此图5中所有数字之和为5×（1+2）.则图2中所有数字之和为 $\frac{1}{3} \times 5 \times (1 + 2)$ ，所以得到等式 $1^{2} + 2^{2} = \frac{1}{3} \times 5 \times (1 + 2)$ .

(1)、探究二：计算 $1^{2} + 2^{2} + 3^{2}$
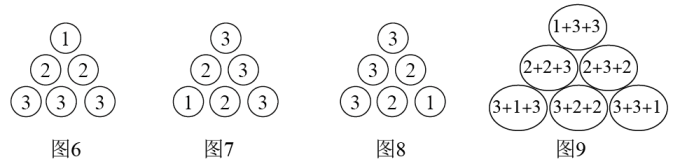
仿照上述方法，将图6按逆时针方向两次旋转得到图7、图8.观察这三个图形，可以发现同一位置圆圈的数字之和都是（如图9），而图9共有个这样的圆圈，因此图9中所有数字之和为.那么图6中所有数字之和为，所以得到等式 $1^{2} + 2^{2} + 3^{2} =$ .（仿照上述方法，写出探究得出的式子）.

(2)、探究三：计算 $1^{2} + 2^{2} + 3^{2} + 4^{2} + 5^{5} + 6^{2} + 7^{2} + 8^{2} + 9^{2} + 1 0^{2} =$ .（仿照上述方法，直接写出结果）.

(3)、【问题解决】 $1^{2} + 2^{2} + 3^{2} + \cdot \cdot \cdot + n^{2} =$ .（仿照上述方法，直接写出探究得出的式子，用含 $n$ 的代数式表示）

(4)、【拓广应用】
计算： $2 6^{2} + 2 7^{2} + 2 8^{2} + \cdot \cdot \cdot + 5 0^{2} =$ .（直接写出结果）

查看试题解析
28. 综合与探究
如图1，已知抛物线 $y = x^{2} + b x + c$ 与x轴相交于点 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ，与y轴交于点C ．

(1)、求抛物线 $y = x^{2} + b x + c$ 及直线 $A C$ 的函数解析式．

(2)、如图2，P是直线 $A C$ 下方的抛物线上的一点，过点P作 $P Q ⊥ x$ 轴于点Q ，交直线AC于点D ，当 $\frac{S_{△ C Q D}}{S_{△ C P D}} = \frac{1}{2}$ 时，求点P的坐标．

(3)、如图3，过点O作 $O M ⊥ A C$ 于点M ，将线段OM所在的直线沿着x轴平移，使得平移后的直线交x轴于点E ，交抛物线于点F ，是否存在点F ，使得四边形 $O M E F$ 是平行四边形?若存在，直接写出点F的坐标；若不存在，请说明理由．

查看试题解析

29. 某数学兴趣小组在探究函数y=|x²-4x+3|的图象和性质时，经历以下几个学习过程：

(1)、列表(完成以下表格)

x	…	-2	-1	0	1	2	3	4	5	6	…
y₁=x²-4x+3	…	15	8		0		0	3		15	…
y=\|x²-4x+3\|	…	15	8		0		0	3		15	…

(2)、描点并画出函数图象草图(在备用图1中描点并画图)

(3)、根据图象完成以下问题

(ⅰ)观察图象

函数y=|x²-4x+3|的图象可由函数y₁=x²-4x+3的图象如何变化得到？

答：．

(ⅱ)数学小组探究发现直线y=8与函数y=|x²-4x+3|的图象交于点E、F，E(-1，8)，F(5，8)，则不等式|x²-4x+3|＞8的解集是；

(4)、设函数y=|x²-4x+3|的图象与x轴交于A、B两点(B位于A的右侧)，与y轴交于点C．

①求直线BC的解析式；

②探究应用：将直线BC沿y轴平移m个单位后与函数y=|x²-4x+3|的图象恰好有3个交点，求此时m的值．

查看试题解析

$x$	$\dots$	$\frac{1}{4}$	$\frac{1}{2}$	$1$	$\frac{3}{2}$	$2$	$\frac{5}{2}$	$\dots$
$y$	$\dots$	$\frac{17}{4}$	$\frac{5}{2}$	$2$	$\frac{13}{6}$	$\frac{5}{2}$	$\frac{29}{10}$	$\dots$

x	0	0.5	1	1.5	2
$x^{3} + 12 x - 15 x - 1$	－1	－5.375	－3	6.875	25

x	1.1	1.2	1.3	1.4
x²+12x﹣15	-0.59	0.84	2.29	3.76

x	…	－3	－2	－1	0	1	2	3	…
y	…	2	1	0	－1	0	1	m	…

备考2024年中考数学核心素养专题九 数与式的探究型问题

一、选择题

二、填空题

三、实践探究题

备考2024年中考数学核心素养专题九数与式的探究型问题