2024年北师大版数学七(下)期中专项复习7 平行线的性质与判定
试卷更新日期:2024-03-10 类型:复习试卷
一、选择题
-
1. 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
 A、∠3=∠A B、∠1=∠2 C、∠D=∠DCE D、∠D+∠ACD=180°2. 下列图形中,由 , 能得到的是( )A、
A、∠3=∠A B、∠1=∠2 C、∠D=∠DCE D、∠D+∠ACD=180°2. 下列图形中,由 , 能得到的是( )A、 B、
B、 C、
C、 D、
D、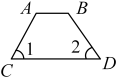 3.
3.如图,下列结论中不正确的是( )
 A、若AD∥BC,则∠1=∠B B、若∠1=∠2,则AD∥BC C、若∠2=∠C,则AE∥CD D、若AE∥CD,则∠1+∠3=180°4. 如图,直线 , 直线 , 若 , 则( )
A、若AD∥BC,则∠1=∠B B、若∠1=∠2,则AD∥BC C、若∠2=∠C,则AE∥CD D、若AE∥CD,则∠1+∠3=180°4. 如图,直线 , 直线 , 若 , 则( ) A、 B、 C、 D、5. 如果两条直线被第三条直线所截,下列判断正确的是( )A、同位角相等 B、同旁内角互补 C、内错角相等 D、不能判断6. 如图,直线 , 被直线所截, , , 若 , 则等于( )
A、 B、 C、 D、5. 如果两条直线被第三条直线所截,下列判断正确的是( )A、同位角相等 B、同旁内角互补 C、内错角相等 D、不能判断6. 如图,直线 , 被直线所截, , , 若 , 则等于( ) A、 B、 C、 D、7. 下列说法中,正确的是( )A、过一点有且只有一条直线与已知直线平行 B、同位角相等 C、从直线外一点到这条直线的垂线段叫做点到直线的距离 D、同一平面内,过一点有且只有一条直线与已知直线垂直8. 如图,下列条件中能判定的是( )
A、 B、 C、 D、7. 下列说法中,正确的是( )A、过一点有且只有一条直线与已知直线平行 B、同位角相等 C、从直线外一点到这条直线的垂线段叫做点到直线的距离 D、同一平面内,过一点有且只有一条直线与已知直线垂直8. 如图,下列条件中能判定的是( ) A、 B、 C、 D、9. 如图, , 平分 , 平分 , , , 则下列结论:
A、 B、 C、 D、9. 如图, , 平分 , 平分 , , , 则下列结论:
;
;
;
.
其中正确结论有个.( )
A、 B、 C、 D、10. 如图,在下列条件中,能够证明的条件是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,将一个直角三角板和一把直尺按如图所示的方式摆放,若 , 则的度数为 .
 12. 如图,已知直线 , , 则 .
12. 如图,已知直线 , , 则 .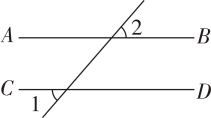 13. 将含角的三角板如图摆放, , 若 , 则的度数是 .
13. 将含角的三角板如图摆放, , 若 , 则的度数是 . 14. 如图是长方形纸带, , 将纸带沿折叠成图 , 再沿折叠成图 , 则图中的度数是 .
14. 如图是长方形纸带, , 将纸带沿折叠成图 , 再沿折叠成图 , 则图中的度数是 . 15. 如图, , 若 , , 则的度数为 .
15. 如图, , 若 , , 则的度数为 .
三、作图题
-
16. 如图,点是内部一点,交于点 .
 (1)、请尺规作图:画出射线 , 使得 , 交直线于点;(2)、请你直接写出与的数量关系: .
(1)、请尺规作图:画出射线 , 使得 , 交直线于点;(2)、请你直接写出与的数量关系: .四、解答题
-
17.
如图,∠1=∠C,AC平分∠DAB,求证:DC∥AB.
 18. 已知:如图 , , 请证明: .
18. 已知:如图 , , 请证明: . 19.
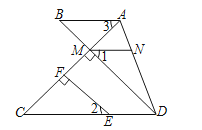
19.已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C,求证:AB∥MN.
 20. 完成下面的证明.
20. 完成下面的证明.如图,已知 , ,
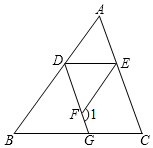
求证:
证明:邻补角定义
且已知
同角的补角相等
▲ ( )
又已知
▲ 等量代换
五、实践探究题
-
21. 已知直线 , 点为直线 , 所确定的平面内的一点,
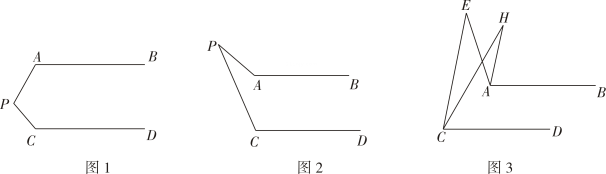 (1)、问题提出:如图 , , 求的度数;(2)、问题迁移:如图 , 写出 , , 之间的数量关系,并说明理由;(3)、问题应用:如图 , :: , , , 求的值.
(1)、问题提出:如图 , , 求的度数;(2)、问题迁移:如图 , 写出 , , 之间的数量关系,并说明理由;(3)、问题应用:如图 , :: , , , 求的值.六、综合题
-
22. 如图,AD∥BC,∠1=∠C,∠B=60°.
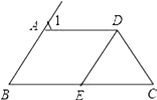 (1)、求∠C的度数;(2)、如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.23. 如图 , 一块直尺和一块含的直角三角板如图放置,其中直尺和直角三角板的斜边平行,我们可以抽象出如图的数学模型: , , , 分别交、于点、、的角平分线交于点 , 为线段上一动点不与、重合 , 连接交于点 .
(1)、求∠C的度数;(2)、如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.23. 如图 , 一块直尺和一块含的直角三角板如图放置,其中直尺和直角三角板的斜边平行,我们可以抽象出如图的数学模型: , , , 分别交、于点、、的角平分线交于点 , 为线段上一动点不与、重合 , 连接交于点 . (1)、当时,求 .(2)、在线段上任意移动时,求 , , 之间的关系.(3)、在(1)的条件下,将绕着点以每秒的速度逆时针旋转,旋转时间为 , 则在旋转过程中,当的其中一边与的某一边平行时,直接写出此时的值.
(1)、当时,求 .(2)、在线段上任意移动时,求 , , 之间的关系.(3)、在(1)的条件下,将绕着点以每秒的速度逆时针旋转,旋转时间为 , 则在旋转过程中,当的其中一边与的某一边平行时,直接写出此时的值.
-
-