2024年北师大版数学七（下）期中专项复习4 整式的乘除法

试卷更新日期：2024-03-10 类型：复习试卷

进入出卷网下载

一、选择题

1. 若 $2 x^{3} - a x^{2} - 5 x + 5 = (2 x^{2} + a x - 1) (x - b) + 3$ ，其中a，b为整数，则a+b的值为（）

A、4 B、0 C、-2 D、-4

查看试题解析
2. 如果 $(2 x + m) (x - 3)$ 展开后的结果不含x的一次项，则m的值是（）

A、6 B、 $\pm 6$ C、0 D、3

查看试题解析
3. （x+5）(x-3)等于（）

A、x² －15 B、x² + 15 C、x² + 2x －15 D、x² － 2x － 15

查看试题解析
4. 下列计算正确的是（）

A、 $(a + b)^{2} = a^{2} + b^{2}$ B、 ${(- 2 a^{3})}^{2} = 4 a^{5}$ C、 $4 a^{3} \cdot 3 a^{2} = 12 a^{5}$ D、 $a^{2} b \div 2 a = 2 a b$

查看试题解析
5. 如果 $(x^{2} - p x + 1) (x^{2} + 6 x - 7)$ 的展开式中不含 $x^{2}$ 项，那么p的值是（）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
6. 下列运算正确的是（）

A、 $x^{3} + x^{3} = x^{6}$ B、 $2 x \cdot 3 x^{2} = 6 x^{3}$ C、 $(2 x)^{3} = 6 x^{3}$ D、 $(2 x^{2} + x) \div x = 2 x$

查看试题解析
7. 下列运算正确的是（）

A、 $x^{4} \cdot x^{4} = x^{16}$ B、 $2 x \cdot 3 x^{2} = 6 x^{3}$ C、 $(2 x)^{3} = 6 x^{3}$ D、 $(2 x^{2} + x) \div x = 2 x$

查看试题解析
8. 计算 $2 x^{2} \cdot (- 3 x^{2})$ 的结果是（）

A、 $- 6 x^{4}$ B、 $6 x^{5}$ C、 $- 2 x^{5}$ D、 $2 x^{6}$

查看试题解析
9. 下列计算正确的是（）

A、x⁵-x³=x² B、3x²y÷3xy=x C、（m²n）³=m⁵n³ D、（x+2）²=x²+4

查看试题解析
10. 若a、b、c是正数，下列各式，从左到右的变形不能用如图验证的是（）

A、（b+c）²＝b²+2bc+c² B、a（b+c）＝ab+ac C、（a+b+c）²＝a²+b²+c²+2ab+2bc+2ac D、a²+2ab＝a（a+2b）

查看试题解析

二、填空题

11. （3a²﹣6ab）÷3a= ．

查看试题解析
12. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下： $\times 2 x = 4 x^{2} - 6 x y + 2 x$ ，则所指的多项式为．

查看试题解析
13. 计算 $3 x^{2} \cdot 2 x y^{2}$ 的结果是．

查看试题解析
14. 已知 $(x + a) (x + b) = x^{2} - 13 x + 36$ ，则 $a^{2} + b^{2}$ 的值是

查看试题解析
15. 小明在计算一道整式乘法的题： $(x - m) (3 x + 5)$ ，因为把“-m”抄成了“+m”，得到的结果是 $3 x^{2} + 11 x + 10$ ，则m的值为．

查看试题解析

三、计算题

16. 计算：

(1)、 ${(- \frac{1}{2})}^{- 2} + {(π - 2)}^{0} - | - 3 |$ ；

(2)、 $12 5^{2} - 124 \times 126$ ；

(3)、 $3 m^{2} \cdot 2 m^{4} - {(2 m^{3})}^{2} + m^{8} \div m^{2}$ ；

(4)、 $(5 a - 4 b) (4 a - 5 b)$ ．

查看试题解析

四、解答题

17. 若 $(x^{2} + p x - \frac{1}{3}) (x^{2} - 3 x + q)$ 的积中不含 $x$ 项与 $x^{3}$ 项，求 $p$ 、 $q$ 的值；

查看试题解析
18. 如果 $x - m$ 与 $3 - x$ 的乘积是一个关于 $x$ 的二次二项式，求 $m$ 的值．

查看试题解析
19. 甲、乙两人共同计算一道整式乘法：（2x+a）（3x+b），由于甲抄错了第一个多项式中a前面的符号，得到的结果为6x²+18x+12；由于乙漏抄了第二个多项中的x的系数，得到的结果为2x²+2x﹣12，请你计算出a、b的值各是多少，并写出这道整式乘法的正确结果．

查看试题解析

五、综合题

20. 亮亮计算一道整式乘法的题（3x-m）（2x-5），由于亮亮在解题过程中，抄错了第一个多项式中m前面的符号，把“-”写成了“＋”，得到的结果为6x²-5x-25．

(1)、求m的值；

(2)、计算这道整式乘法的正确结果．

查看试题解析
21. 我们知道，图形是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数量关系，对几何图形做出代数解释和用几何图形的面积表示代数恒等式是互逆的．课本上由拼图用几何图形的面积来验证了乘法公式，一些代数恒等式也能用这种形式表示，例如（2a＋b）（a＋b）＝2a²＋3ab＋b²就可以用图①或图②等图形的面积表示．

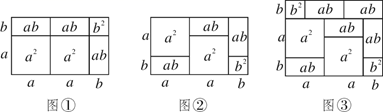(1)、填一填：请写出图③所表示的代数恒等式：；

(2)、画一画：试画出一个几何图形，使它的面积能表示：（a＋b）（a＋3b）＝a²＋4ab＋3b².

查看试题解析