2024年北师大版数学七（下）期中专项复习5 整式的混合运算

试卷更新日期：2024-03-10 类型：复习试卷

进入出卷网下载

一、选择题

1. 一个正方形的边长为 $a c m$ ，若它的边长增加 $4 c m$ ，则面积增加了 $c m^{2}$ ．（）

A、 $16$ B、 $8 a$ C、 $(16 + 4 a)$ D、 $(16 + 8 a)$

查看试题解析
2. 已知：a＋b＝m，ab＝－4，化简（a－2）（b－2）的结果是（）.

A、6 B、2m－8 C、2m D、－2m

查看试题解析
3. 某商品涨价30%后欲恢复原价，则必须下降的百分数约为（　　）

A、20% B、21% C、22% D、23%

查看试题解析
4. 已知a²+a﹣3=0，那么a²（a+4）的值是（　　）

A、9 B、﹣12 C、﹣18 D、﹣15

查看试题解析
5. 如图，在长为3a+2，宽为2b-1的长方形铁片上，挖去长为2a+4，宽为b的小长方形铁片，则剩余部分面积是（）

A、6ab-3a+4b B、4ab-3a-2 C、6ab-3a+8b-2 D、4ab-3a+8b-2

查看试题解析
6. 任意写下一个两位数，用它两个数位的数字和的10倍减去这个两位数，得差．然后对差重复这一运算程序……，以下结论正确的是（）

A、差是7的倍数 B、差是8的倍数 C、差是9的倍数 D、差是10的倍数

查看试题解析
7. 【观察】① $(x - 1) (x + 1) = x^{2} - 1$ ；
② $(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；

③ $(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；

……

【归纳】由此可得： $(x - 1) (x^{n} + x^{n - 1} + x^{n - 2} + \dots + x + 1) = x^{n + 1} - 1$ ；

【应用】请运用上面的结论，计算： $2^{2023} + 2^{2022} + 2^{2021} + \dots + 2^{2} + 2 + 1 =$ （）

A、 $2^{2023} - 1$ B、 $2^{2024} - 1$ C、 $2^{2024}$ D、 $2^{2025} - 1$

查看试题解析
8. 若M＝（x - 2）（x - 5），N＝（x - 2）（x - 6），则M与N的关系为（）

A、M＝N B、M＞N C、M＜N D、不能确定

查看试题解析
9. 下列运算正确的是（）

A、 $x^{2} \cdot x^{5} = x^{10}$ B、 ${(- x^{2})}^{5} = x^{10}$ C、 $x^{5} + x^{2} = x^{7}$ D、 $x^{5} \div x^{2} = x^{3} (x \neq 0)$

查看试题解析
10. 下列运算中，正确的是（）

A、a³·a²=a⁶ B、(-a)²·a³=-a⁵ C、-(-a)³=-a³ D、[(-a)³]²=a⁶

查看试题解析

二、填空题

11. 输入 $x$ ，按如下图所示的程序进行计算后，请用含 $x$ 的式子表示输出的结果为．

查看试题解析
12. 计算2022⁰+( $- \frac{1}{2}$ )-1= ．

查看试题解析
13. 对于任何实数，我们规定符号 $| \begin{array}{l} a c \\ b d \end{array} |$ 的意义 $| \begin{array}{l} a c \\ b d \end{array} |$ =ad-bc，按照这个规定请你计算：当 $x^{2} - 3 x + 1 = 0$ 时，求 $| \begin{array}{l} x + 1 x - 2 \\ 3 x x - 1 \end{array} |$ 的值．

查看试题解析
14. 某天数学课上，学习了整式的除法运算，放学后，小明回到家拿出课堂笔记，认真地复习课上学习的内容，他突然发现一道三项式除法运算题：
$(21 x^{4} y^{3} -$ $+ 7 x^{2} y^{2}) \div (- 7 x^{2} y) = - 3 x^{2} y^{2} + 5 x y - y$ 被除式的第二项中被钢笔水弄污了（还能看到前面的运算符号），你能算出被污染的内容是．

查看试题解析
15. 已知7x³y²与一个多项式之积是28x⁴y²+7x⁴y³﹣21x³y² ，则这个多项式是　

查看试题解析

三、计算题

16. 计算：

(1)、 $(π - 2)^{0} - | 8 | + (\frac{1}{3})^{- 2}$ ；

(2)、 $(2 x)^{3} \cdot (- 3 x y^{2}) \div (- 2 x^{2} y^{2})$ ；

(3)、 $(4 - x)^{2} - (x - 2) (x + 3)$ ；

(4)、 $12 5^{2} - 124 \times 126 . ($ 请用简便运算 $)$

查看试题解析

四、解答题

17. 先化简，再求值： $[(x - 2 y)^{2} + (3 x - y) (3 x + y) - 3 y^{2}] \div (- 2 x)$ ，其中 $x$ 、 $y$ 满足 $x = 1$ ， $y = - 3$ ．

查看试题解析

五、综合题

18. 如图1，有足够多的1号大正方形，2号小正方形、3号长方形的卡片，某数学课后活动小组的两名成员，分别选取了1号、2号、3号卡片各1张、2张、3张，拼成了如图2的一个不重叠无缝障长方形．

(1)、【观察推理】观察图2，小军、小芳分别用长方形面积公式，拼图所用三种卡片数量得出了图2的面积的表示方法，因此得出了含有 $a$ 、 $b$ 的一个等式：．

(2)、【尝试探究】小军想设计一个长为 $(3 a + b)$ ，宽为 $(a + 3 b)$ 的长方形，小芳很快告知了小军所需的1号、2号、3号卡片的张数，请你用所学知识推算出1号、2号、3号卡片的数量．

(3)、【综合应用】小芳提议：在1号卡片的四个角上各裁去一个小正方形卡片（剪去部分不再使用）．再沿虚线折叠、粘合（如图3），能制作出一个无盖长方体盒子．若 $a = 3$ 分米，小正方形的边长记为 $c$ 分米（ $c$ 的值可变化），无盖长方体的体积记为 $V$ （ $分米^{3}$ ），
①无盖长方体的体积 $V =$ （用含 $c$ 的代数式表示）；

②两人把 $c$ 的多种情况代入上式，发现当 $c = 0.4$ 时， $V =$ $分米^{3}$ ，当 $c = 1$ 时， $V =$ $分米^{3}$ ；他们找老师帮绘制出了 $V$ 与 $c$ 的关系图像（如图4），最终证实了当 $c = \frac{1}{6} a$ 时， $V$ 最大，最大值= $分米^{3}$ ；

③借助以上信息，可得 $V$ 随着 $c$ 的变化而变化的情况是：．

查看试题解析
19. 如图，阴影部分是一个“ $T$ ”型．

(1)、用含 $x$ ， $y$ 的代数式表示“ $T$ ”型图形的面积并化简；

(2)、若 $x = 5$ 米， $y = 15$ 米，“ $T$ ”型区域铺上价格为每平方米20元的草坪，请计算草坪的造价．

查看试题解析
20. 已知 $A = {(x + y)}^{2} - {(x - y)}^{2}$ ， $B = (2 x^{2} y + 5 x y^{2}) \div x y - 4 x y$ ．

(1)、求 $A$ 和 $B$ ；

(2)、若变量 $x$ ， $y$ 满足 $A + B = 3$ ，求 $y$ 与 $x$ 的关系式；

(3)、在（2）的条件下，求 $4^{x} \cdot 3 2^{y}$ 的值．

查看试题解析
21. 如图，某校有一块长为 $(3 a + b)$ 米，宽为 $(2 a + b)$ 米的长方形空地，中间是边长 $(a + b)$ 米的正方形草坪，其余为活动场地，学校计划将活动场地（阴影部分）进行硬化．

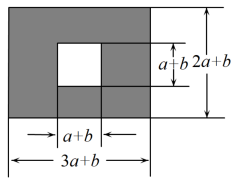(1)、用含 $a$ ， $b$ 的代数式表示需要硬化的面积并化简；

(2)、当 $a = 5$ ， $b = 2$ 时，求需要硬化的面积．

查看试题解析
22. 杨辉三角是一个由数字排列成等腰三角形数表，一般形式如图所示，其中每一横行都表示 ${(a + b)}^{n}$ （此处 $n = 0$ ， $1$ ， $2$ ， $3$ ， $4$ ， $5$ ， $6$ ）的展开式中的系数，杨辉三角最本质的特征是，它的两条斜边都是由数字 $1$ 组成的，而其余的数则是等于它“肩”上的两个数之和． $1$
$1$ $1$
$1$ $2$    $1$
$1$ $3$    $3$    $1$
$1$ $4$    $6$    $4$    $1$
$1$ $5$    $10$    $10$    $5$    $1$
$1$ $6$    $15$    $20$    $15$    $6$    $1$
${(a + b)}^{0} = 1$
${(a + b)}^{1} = a + b$
${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$
${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$
${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$
${(a + b)}^{5} = a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}$
${(a + b)}^{6} = a^{6} + 6 a^{5} b + 15 a^{4} b^{2} + 20 a^{2} b^{3} + 15 a^{2} b^{4} + 6 a b^{5} + b^{6}$
上图的构成规律你看懂了吗？

(1)、请你直接写出 ${(a + b)}^{7} =$ ．

(2)、杨辉三角还有另一个特征
从第二行到第五行，每一行数字组成的数（如第三行为 $121$ ）都是上一行的数与积．

(3)、由此你可写出 $11^{5}$ = ．

查看试题解析