备考2024年中考数学核心素养专题八 实验操作型问题
试卷更新日期:2024-03-10 类型:二轮复习
一、选择题
-
1. 在烧开水时,水温达到就会沸腾,如表是某同学做“观察水的沸腾”实验时所记录的两个变量时间和温度的数据,时间每增加 , 水的温度就升高 . 在水烧开之前(即 , 温度与时间之间的关系式为( )
0
2
4
6
8
10
30
44
58
72
86
100
A、 B、 C、 D、2. 小颖同学受“阿基米德测皇冠的故事”启发,做了测量土豆体积的实验.如图,将一个不规则的土豆从水中匀速提起,如果水箱里水面的高度是 , 把土豆从水箱中匀速提起的时间是 , 那么能够表示与之间函数关系的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 如图,在实验课上,小亮利用同一块木板,测量了小车从木板顶部下滑的时间与支撑物的高度 , 得到如下表所示的数据.下列结论不正确的是( )
3. 如图,在实验课上,小亮利用同一块木板,测量了小车从木板顶部下滑的时间与支撑物的高度 , 得到如下表所示的数据.下列结论不正确的是( )木板的支撑物高度
…
下滑时间
…
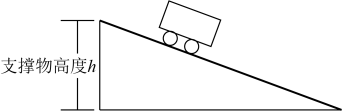 A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短4. 在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图象(不计绳重和摩擦),请你根据图象判断以下结论正确的序号有( )
A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短4. 在物理实验课上,小鹏利用滑轮组及相关器材进行实验,他把得到的拉力F(N)和所悬挂物体的重力G(N)的几组数据用电脑绘制成如图象(不计绳重和摩擦),请你根据图象判断以下结论正确的序号有( )
①物体的拉力随着重力的增加而增大;
②当物体的重力G=7N时,拉力F=2.2N;
③拉力F与重力G成正比例函数关系;
④当滑轮组不悬挂物体时,所用拉力为0.5N .
A、①② B、②④ C、①④ D、③④5. 加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可得到最佳加工时间为( ) A、4.25分钟 B、4.00分钟 C、3.75分钟 D、3.50分钟6. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为10cm , 像距为15cm , 蜡烛火焰倒立的像的高度是8cm , 则蜡烛火焰的高度是( )cm .
A、4.25分钟 B、4.00分钟 C、3.75分钟 D、3.50分钟6. 大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为10cm , 像距为15cm , 蜡烛火焰倒立的像的高度是8cm , 则蜡烛火焰的高度是( )cm . A、 B、6 C、 D、87. 在一次实验操作中,如图①是一个长和宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6;现将图①容器向右倾倒,按图放置,发现此时水面恰好触到容器口边缘,则图②中水面高度为( )
A、 B、6 C、 D、87. 在一次实验操作中,如图①是一个长和宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6;现将图①容器向右倾倒,按图放置,发现此时水面恰好触到容器口边缘,则图②中水面高度为( )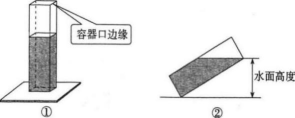 A、 B、 C、 D、8. 光线从空气射入水中会发生折射现象,如图①所示.小华为了观察光线的折射现象,设计了图②所示的实验:通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块.图③是实验的示意图,点A,C,B在同一直线上,下列各角中,∠PDM的对顶角是 ( )
A、 B、 C、 D、8. 光线从空气射入水中会发生折射现象,如图①所示.小华为了观察光线的折射现象,设计了图②所示的实验:通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块.图③是实验的示意图,点A,C,B在同一直线上,下列各角中,∠PDM的对顶角是 ( ) A、∠BCD B、∠FDB C、∠BDN D、∠CDB9. 小举在探究全等三角形判定方法,已知如图,ABC,他通过尺规作图、裁剪、重合的操作,证实一种判定方法.以下是小举的操作过程:
A、∠BCD B、∠FDB C、∠BDN D、∠CDB9. 小举在探究全等三角形判定方法,已知如图,ABC,他通过尺规作图、裁剪、重合的操作,证实一种判定方法.以下是小举的操作过程:第一步:尺规作图.
作法:(1)作射线M;(2)以点B为圆心,任意长为半径画弧,分别交BA,BC于点E,D;(3)以点为圆心,BD长为半径画弧,交M于点P;(4)以点P为圆心,DE长为半径画弧,在M的上方交(3)中所画弧于点Q;(5)过点Q作射线BˊN;(6)以点为圆心,BC长为半径画弧,交M于点;(7)以点为圆心,BA长为半径画弧,交N于点;(8)连接 .
第二步:把作出的剪下来,放到上.
第三步:观察发现和重合.
∴ .
根据小举的操作过程可知,小举是在探究( )
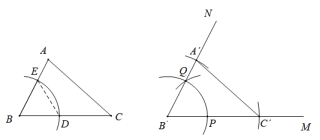 A、基本事实SSS B、基本事实ASA C、基本事实SAS D、定理AAS
A、基本事实SSS B、基本事实ASA C、基本事实SAS D、定理AAS二、填空题
-
10. 【动手实践】小明学习了课本“实验与探究”后做了如下探索:他按图1方法把边长为5厘米和3厘米的两个正方形切割成5块,按图2方式拼成的一个大正方形,则大正方形的边长是厘米.
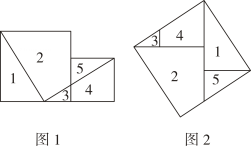
三、作图题
-
11. 某小组在做“探究水的沸腾”实验时,实验装置如图①所示.实验中温度y()和时间x(分钟)变化的数据记录如下表:
时间(分钟)
0
5
10
15
20
温度
25
40
55
70
85
 (1)、在如图②所示的平面直角坐标系中描出上表的各点,用光滑的线连接:(2)、许你根据表中的数据及画出的图象,确定与之间的函数解析式;(3)、若温度恰好达到时水开始沸腾,请求出从计时开始多长时间后水开始沸腾.12. 阅读与思考
(1)、在如图②所示的平面直角坐标系中描出上表的各点,用光滑的线连接:(2)、许你根据表中的数据及画出的图象,确定与之间的函数解析式;(3)、若温度恰好达到时水开始沸腾,请求出从计时开始多长时间后水开始沸腾.12. 阅读与思考下面是小宇同学的一篇日记,请仔细阅读并完成相应的任务.
在物理活动课上,我们“博学”小组的同学,参加了一次“探究电功率P与电阻R之间的函数关系”的活动.

第一步,实验测量.根据物理知识,改变电阻R的大小,通过测量电路中的电流,计算电功率P.
第二步,整理数据.
…
3
6
9
12
15
…
…
3
1.5
1
0.75
0.7
…
第三步,描点连线.以R的数值为横坐标,对应P的数值为纵坐标在平面直角坐标系中描出以表中数值为坐标的各点,并用光滑的曲线顺次连接这些点.
在数据分析时,我发现一个数据有错误,重新测量计算后,证明了我的猜想正确,并修改了表中这个数据.实验结束后,大家都有很多收获,每人都撰写了日记.
任务:
 (1)、表格中错误的数据是 , P与R的函数表达式为;(2)、在平面直角坐标系中,画出P与R的函数图象;(3)、结合图象,直接写出P大于6W时R的取值范围.
(1)、表格中错误的数据是 , P与R的函数表达式为;(2)、在平面直角坐标系中,画出P与R的函数图象;(3)、结合图象,直接写出P大于6W时R的取值范围.四、解答题
-
13. 科学家实验发现,声音在不同气温下传播的速度不同,声音在空气中的传播速度随温度的变化而有规律的变化.七(1)班社团通过查阅资料发现,声音在空气中传播的速度和气温的变化存在如下的关系:
气温t/℃
0
1
2
3
4
5
声音在空气中的传播速度v/(m/s)
331
331.6
332.2
332.8
333.4
334
(1)、在这个变化过程中,是自变量,是因变量;(2)、声音在空气中的传播速度v/(m/s)与气温t(℃)的关系式可以表示为;(3)、某日的气温为20℃,小乐看到烟花燃放5s后才听到声响,那么小乐与燃放烟花所在地大约相距多远?14. 如图,当弹簧受到重力的作用时会伸长,某学习小组用实验的方式研究了一个弹簧的长度与所挂物体重量之间的关系,并对每组数据进行了记录:物体的重量
0
1
2
3
4
5
…
弹簧的长度
9
11
13
15
17
19
…
 (1)、上表所表示的变量之间的关系中,自变量是 , 因变量是 .(2)、当弹簧不悬挂重物时长度为cm,物体重量每增加 , 弹簧长度y增加cm;(3)、直接写出y与x的关系式: .(4)、当所挂物重为时,弹簧的长度为cm;(5)、这根弹簧的弹性限度(即弹簧最长可以被拉长到的长度,超过这个长度,弹簧将失去弹性)为 , 则在弹性限度之内,该弹簧最多可以挂多重的物体?15. “漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.
(1)、上表所表示的变量之间的关系中,自变量是 , 因变量是 .(2)、当弹簧不悬挂重物时长度为cm,物体重量每增加 , 弹簧长度y增加cm;(3)、直接写出y与x的关系式: .(4)、当所挂物重为时,弹簧的长度为cm;(5)、这根弹簧的弹性限度(即弹簧最长可以被拉长到的长度,超过这个长度,弹簧将失去弹性)为 , 则在弹性限度之内,该弹簧最多可以挂多重的物体?15. “漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体. (1)、表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:
(1)、表是实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的数据:时间x(小时)
1
2
3
4
5
圆柱体容器液面高度y(厘米)
6
10
14
18
22
在如图②所示的直角坐标系中描出上表的各点,并用线段连接.
(2)、请根据(1)中的数据确定y与x之间的函数表达式;(3)、如果本次实验记录的开始时间是上午9:00,那么当圆柱体容器液面高度达到12厘米时是几点?16. 根据以下素材,探索完成任务.如何利用“漏壶”探索时间
素材1
“漏壶”是一种古代计时器,数学兴趣小组根据“漏壶”的原理制作了如图①所示的液体漏壶,漏壶是由一个圆锥和一个圆柱(圆柱的最大高度是27厘米)组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.

素材2
实验记录的圆柱体容器液面高度y(厘米)与时间x(小时)的部分数据如右表所示:

问题解决
任务1
描点连线
在如图2所示的直角坐标系中描出上表的各点,用光滑的线连接;
任务2
确定关系
请确定一个合理的y与x之间函数关系式,并求出自变量x的取值范围;
任务3
拟定计时方案
小明想要设计出圆柱体容器液面高度和计时时长都是整数的计时器,且圆柱体容器液面高度需满足10厘米~20厘米,请求出所有符合要求的方案.
17. 在数学实验课上,小莹将含角的直角三角尺分别以两个直角边为轴旋转一周,得到甲、乙两个圆锥,并用作图软件Geogebra画出如下示意图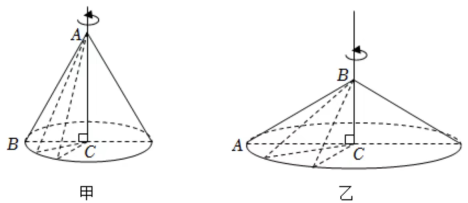
小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边旋转得到,所以它们的侧面积相等.”
你认同小亮的说法吗?请说明理由.
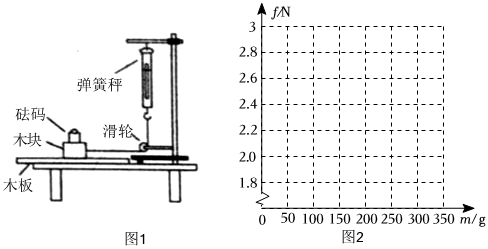
18. 通过小学的学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之间会产生阻碍物体运动的力、像这样的力是摩擦力.小明利用如图1所示的装置测量在不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成如表:砝码的质量m/g
0
50
100
150
200
250
滑动摩擦力f/N
1.8
2.0
2.2
2.4
2.6
2.8
 (1)、请在图2的平面直角坐标系内,描出六次测量的有序数对(m , f)所对应的六个点;(2)、这些点是否在一条直线上?如果是,请确定f与m的关系式;如果不是,请说明理由;(3)、在某次实验中,测得木块受到的摩擦力为4.2N , 则此时砝码的质量是多少?(4)、在实验过程中,当砝码的质量为100g~800g时,请直接写出木块受到的摩擦力的最大值和最小值分别为多少?19. 为激发学生们对科技的好奇心和探索欲,培养学生的创新意识和创新精神,某学校开展了“智能小车实验探究”活动.某小组观察探究小车运动中的函数关系,如图,在一条长为的水平直线轨道上,放置一辆长为的智能小车,开始时小车左端与处挡板重合,然后以的速度匀速向右行驶,当小车接触到处的挡板时因为要改变方向需停顿 , 然后以相同的速度返回,至再次与处的挡板接触时小车停止运动.在这个过程中,设小车的右端与处挡板的距离为 , 小车出发后的时间为 , 请根据所给条件解决下列问题:
(1)、请在图2的平面直角坐标系内,描出六次测量的有序数对(m , f)所对应的六个点;(2)、这些点是否在一条直线上?如果是,请确定f与m的关系式;如果不是,请说明理由;(3)、在某次实验中,测得木块受到的摩擦力为4.2N , 则此时砝码的质量是多少?(4)、在实验过程中,当砝码的质量为100g~800g时,请直接写出木块受到的摩擦力的最大值和最小值分别为多少?19. 为激发学生们对科技的好奇心和探索欲,培养学生的创新意识和创新精神,某学校开展了“智能小车实验探究”活动.某小组观察探究小车运动中的函数关系,如图,在一条长为的水平直线轨道上,放置一辆长为的智能小车,开始时小车左端与处挡板重合,然后以的速度匀速向右行驶,当小车接触到处的挡板时因为要改变方向需停顿 , 然后以相同的速度返回,至再次与处的挡板接触时小车停止运动.在这个过程中,设小车的右端与处挡板的距离为 , 小车出发后的时间为 , 请根据所给条件解决下列问题: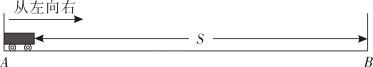 (1)、小车运动时间为时,的值为;(2)、小车从处驶向处的过程中,求与的函数表达式;(3)、当小车左端与处挡板的距离比小车右端与处挡板距离的2倍多时,请求出的值.20. 数学来源于生活,生活中处处有数学,用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论.现有a克糖水,其中含有b克糖(a>b>0),则糖水的浓度(即糖的质量与糖水的质量比)为 .(1)、糖水实验一:加入m克水,则糖水的浓度为 . 生活经验告诉我们,糖水加水后会变淡,由此可以写出一个不等式 , 我们趣称为“糖水不等式”.(2)、糖水实验二:
(1)、小车运动时间为时,的值为;(2)、小车从处驶向处的过程中,求与的函数表达式;(3)、当小车左端与处挡板的距离比小车右端与处挡板距离的2倍多时,请求出的值.20. 数学来源于生活,生活中处处有数学,用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论.现有a克糖水,其中含有b克糖(a>b>0),则糖水的浓度(即糖的质量与糖水的质量比)为 .(1)、糖水实验一:加入m克水,则糖水的浓度为 . 生活经验告诉我们,糖水加水后会变淡,由此可以写出一个不等式 , 我们趣称为“糖水不等式”.(2)、糖水实验二:将“糖水实验一”中的“加入m克水”改为“加入m克糖”,则糖水的浓度为 . 根据生活经验,请你写出一个新的“糖水不等式” .
(3)、请结合(2)探究得到的结论尝试证明:设a、b、c为△ABC三边的长,求证:.
五、实践探究题
-
21. 【背景】在一次物理实验中,小冉同学用一固定电压为的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡(灯丝的阻值)亮度的实验(如图),已知串联电路中,电流与电阻之间关系为 , 通过实验得出如下数据:
…
1
3
4
6
…
…
4
3
2.4
2
…
 (1)、 , ;(2)、【探究】根据以上实验,构建出函数 , 结合表格信息,探究函数的图象与性质.
(1)、 , ;(2)、【探究】根据以上实验,构建出函数 , 结合表格信息,探究函数的图象与性质.①在平面直角坐标系中画出对应函数的图象;

②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)、【拓展】结合(2)中函数图象分析,当时,的解集为 .22. 刻漏是人类最早制造的不完全依赖天象、相对独立运行的计时仪器.刻漏以水等液体(也有少数例外,如水银或沙等)为工作物质,根据流水的量与流逝时间的对应关系,通过漏壶中的水量变化来度量时间的.我国使用刻漏的时间非常早,最早可追溯到中国历史上第一个王朝—夏朝(大约公元前2070年),约在汉武帝时期发明了浮箭漏.如图所示为单级浮箭漏示意图.某兴趣小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究: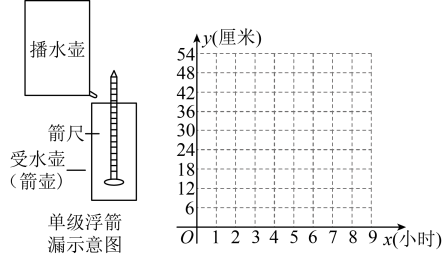
【实验观察】实验小组通过观察,每1小时记录一次箭尺读数,得到如表:
供水时间x(小时)
0
1
2
3
4
箭尺读数y(厘米)
6
12
18
24
30
【探索发现】
(1)、在所给的平面直角坐标系中,描出以供水时间x为横坐标,箭尺读数y为纵坐标的各点.(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.(3)、供水时间达到10小时时,箭尺的读数为多少厘米?(4)、如果本次实验记录的开始时间是上午 , 那当箭尺读数为96厘米时是几点钟?(箭尺最大读数为100厘米)23. 为研究某种化学试剂的挥发情况,某研究团队在两种不同的场景下做对比实验,收集了该试剂挥发过程中剩余质量克随时间分钟变化的数据 , 并分别绘制在直角坐标系中,如图所示.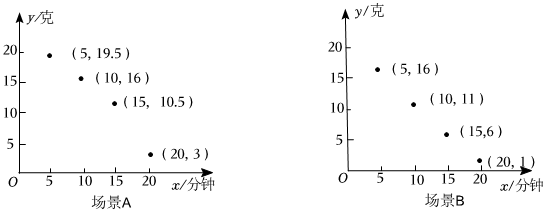 (1)、从 , , 中,选择适当的函数模型分别模拟两种场景下随变化的函数关系,并求出相应的函数表达式;(2)、查阅文献可知,该化学试剂发挥作用的最低质量为克在上述实验中,该化学试剂在哪种场景下发挥作用的时间更长?24. 【发现问题】如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE、DF的反向延长线交于主光轴MN上一点P.
(1)、从 , , 中,选择适当的函数模型分别模拟两种场景下随变化的函数关系,并求出相应的函数表达式;(2)、查阅文献可知,该化学试剂发挥作用的最低质量为克在上述实验中,该化学试剂在哪种场景下发挥作用的时间更长?24. 【发现问题】如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE、DF的反向延长线交于主光轴MN上一点P.
【提出问题】小明提出:∠BPD、∠ABP和∠CDP三个角之间存在着什么样的数量关系?
【分析问题】我们学习过平行线的性质,利用平行线的性质可以把∠BPD分成两部分进行研究.
(1)、【解决问题】请你帮小明解决这个问题,并说明理由.(2)、【举一反三】①如图①,若∠ABE=150°,∠CDF=170°,则∠EPF=度.②如图②,已知AB∥CD,点E、F分别是AB、CD上的点,点P位于AB上方,∠PEB=α,∠PFD=β.用含α和β的代数式表示下列各角.
∠P的大小为 . 如图③,在图②的基础上,若EQ和FQ分别平分∠PEB和∠PFD,则∠Q的大小为 .
25. 【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律
图1 图2
【同题解决】如图2.小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电简的灯泡在点G处,手电简的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点F到地面的高度 , 点A、点C到平面镜B点的距离相等.图中点A,B,C,D在同一条直线上.求灯泡到地面的高度 .
26. 类比一次函数和反比例函数的学习经验,某数学实验小组尝试探究“的函数图象与性质”,进行了如下活动.(1)、【小组合作 讨论交流】同学甲说:“我们可以从表达式分析,猜想图像位置.”
同学乙回应道:“是的,因为自变量x的取值范围是 , 所以图像与y轴不相交.”
同学丙补充说:“又因为函数值y大于0,所以图像一定在第象限.”
……
(2)、【独立操作 探究性质】在平面直角坐标系中,画出的图像.

结合图像,描述函数图象与性质:
①函数的图像是两条曲线;
②该函数图象关于 ▲ 对称;
③图像的增减性是 ▲ ;
④同学丁说:“将第二象限的曲线绕原点顺时针旋转后,与第一象限的曲线重合.”请你判断同学丁的说法是否正确?若错误,举出反例;若正确,请说明理由.
(3)、【拓展探究 综合应用】直接写出不等式的解集是.
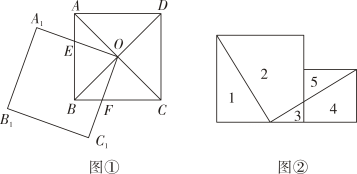
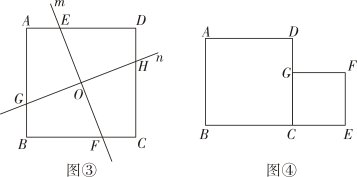
27. 同学们还记得吗?图①,图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形.受这两个图形的启发,数学兴趣小组提出了以下三个问题,请你回答:
 (1)、【问题一】
(1)、【问题一】如图①,正方形ABCD的对角线相交于点O,点O又是正方形的一个顶点,交AB于点E,交BC于点F,则AE与BF的数量关系为;
(2)、【问题二】受图①启发,兴趣小组画出了图③:直线m、n都经过正方形ABCD的对角线交点O,直线m分别与AD、BC交于点E、F,直线n分别与AB、CD交于点G、H,且m⊥n,若正方形ABCD边长为8,求四边形OEAG的面积;
(3)、【问题三】受图②启发,兴趣小组画出了图④:正方形CEFG的顶点G在正方形ABCD的边CD上,顶点E在BC的延长线上,且BC=6,CE=2.在直线BE上是否存在点P,使得△APF为直角三角形?若存在,求出BP的长度;若不存在,说明理由.
28.【问题情境】:一副三角尺和中, , , , 在数学课上,同学们用这样的一副三角尺进行摆放,将三角尺的直角顶点放在三角尺内部,直角边与交于点 , 直角边与交于点 .

【实验探究】:
(1)、如图 , 勤学小组的同学发现任意改变三角尺的位置,的度数都为 , 请说明理由;(2)、如图 , 善思小组的同学改变三角尺的位置,将直角顶点放在的平分线上,测量发现 , 请证明此结论.六、综合题
-
29. 科学家实验发现,声音在不同气温下传播的速度不同,声音在空气中的传播速度随温度的变化而有规律的变化.某兴趣小组为探究空气的温度与声音在空气中传播的速度y(米/秒)之间的关系,在标准实验室里进行了多次实验.如表为实验时记录的一些数据.
温度
0
5
10
15
20
音速y(米/秒)
331
334
337
340
343
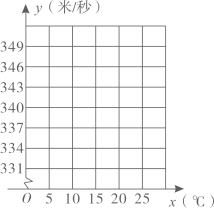 (1)、在如图的平面直角坐标系中,横轴为气温 , 纵轴为声音在空气中传播的速度y(米/秒),描出以表格中数据为坐标的各点;(2)、观察所描各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由;(3)、当气温是时,求声音在空气中传播的速度;30. 为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油实验,并把实验的数据记录 下来,制成下表:
(1)、在如图的平面直角坐标系中,横轴为气温 , 纵轴为声音在空气中传播的速度y(米/秒),描出以表格中数据为坐标的各点;(2)、观察所描各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由;(3)、当气温是时,求声音在空气中传播的速度;30. 为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油实验,并把实验的数据记录 下来,制成下表:汽车行驶时间x(h)
0
1
2
3
…
邮箱剩余油量y(L)
100
94
88
82
…
(1)、根据上表的数据,请写出y与x的之间的关系式:;(2)、如果汽车油箱中剩余油量为46L,则汽车行驶了多少小时?(3)、如果该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公 路上均匀行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗?为什 么?31. 一直以来,人们力图探寻地球内部的奥秘,科学家做了大量的模拟实验后发现:地表以下岩层的温度随着所处深度的变化而变化,在某个地点与之间的关系可近似地表示为 . (1)、根据关系式,下表列出部分因变量与自变量的对应值,请补充表中所缺的数据;
(1)、根据关系式,下表列出部分因变量与自变量的对应值,请补充表中所缺的数据;所处深度
2
3
4
5
6
7
岩层的温度
90
125
195
265
(2)、当所处深度每增加 , 岩层的温度是怎样变化的?(3)、当岩层的温度达到时,根据上述关系式,求所处的深度.32. 某学校STEAM社团在进行项目化学习时,根据古代的沙漏模型(图1)制作了一套“沙漏计时装置”,该装置由沙漏和精密电子秤组成,电子秤上放置盛沙容器.沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内,可以通过读取电子秤的读数计算时间(假设沙子足够).该实验小组从函数角度进行了如下实验探究:实验观察:实验小组通过观察,每两小时记录一次电子秤读数,得到下表.
漏沙时间x(h)
0
2
4
6
8
电子秤读数y(克)
6
18
30
42
54
 (1)、探索发现:建立平面直角坐标系,如图2,横轴表示漏沙时间x,纵坐标表示精密电子称的读数y,描出以表中的数据为坐标的各点.(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,请你建立适当的函数模型,并求出函数表达式,如果不在同一条直线上,请说明理由.(3)、结论应用:应用上述发现的规律估算:若漏沙时间为9小时,精密电子称的读数为多少?(4)、若本次实验开始记录的时间是上午7:30,当精密电子秤的读数为72克时是几点钟?33. 如图,某物理实验装置由一个带刻度的无盖圆柱体玻璃筒和一个带托盘的活塞组成,该装置竖直放置时,活塞受到托盘中重物的压力向下压缩装置内的空气.某同学试着放上不同质量的物体,并根据筒侧的刻度记录活塞到筒底的距离,得到下面5组数据:
(1)、探索发现:建立平面直角坐标系,如图2,横轴表示漏沙时间x,纵坐标表示精密电子称的读数y,描出以表中的数据为坐标的各点.(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,请你建立适当的函数模型,并求出函数表达式,如果不在同一条直线上,请说明理由.(3)、结论应用:应用上述发现的规律估算:若漏沙时间为9小时,精密电子称的读数为多少?(4)、若本次实验开始记录的时间是上午7:30,当精密电子秤的读数为72克时是几点钟?33. 如图,某物理实验装置由一个带刻度的无盖圆柱体玻璃筒和一个带托盘的活塞组成,该装置竖直放置时,活塞受到托盘中重物的压力向下压缩装置内的空气.某同学试着放上不同质量的物体,并根据筒侧的刻度记录活塞到筒底的距离,得到下面5组数据:重物质量m/kg
2
3
4
6
8
活塞到桶底的距离h/cm
24
16
12
8
6
 (1)、以表中各组数据对应值为点的坐标,在如图直角坐标系中描出相应的点并用光滑的曲线连接.(2)、能否用学过的函数刻画变量h和m之间的关系?如果能,请求出h关于m的解析式;如果不能,请说明理由.(3)、要使活塞到筒底的距离大于5,请直接写出在托盘中放入重物的质量m的取值范围.34. 小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)、以表中各组数据对应值为点的坐标,在如图直角坐标系中描出相应的点并用光滑的曲线连接.(2)、能否用学过的函数刻画变量h和m之间的关系?如果能,请求出h关于m的解析式;如果不能,请说明理由.(3)、要使活塞到筒底的距离大于5,请直接写出在托盘中放入重物的质量m的取值范围.34. 小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答: (1)、如图1,白天在阳光下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .
(1)、如图1,白天在阳光下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .①若木杆 的长为 ,则其影子 的长为 ;
②在同一时刻同一地点,将另一根木杆 直立于地面,请画出表示此时木杆 在地面上影子的线段 ;
(2)、如图2,夜晚在路灯下,小彬将木杆 水平放置,此时木杆在水平地面上的影子为线段 .①请在图中画出表示路灯灯泡位置的点 ;
②若木杆 的长为 ,经测量木杆 距离地面 ,其影子 的长为 ,则路灯 距离地面的高度为 .
35. 翻开数学发展史,我们就知道数学不仅是抽象、严谨的,还有另外一面,人类从结绳计数开始就在进行着数学实验,并且通过实验不断发展数学,可见,数学实验不仅是数学家研究数学的方式,也是学生学习数学的一种重要方式,在某次数学社团活动中,几位同学利用三角板进行了如下的实数学验,请大家在这一数学实验的基础上思考并回答相关问题:几位同学把两块完全相同的等腰直角三角板按图1方式摆放,已知 , , , , , 线段在直线上,点F在线段上,点A与点D重合. (1)、 , ;(2)、将三角板的直角顶点F沿方向滑动,同时顶点D沿方向在射线上滑动,如图2.
(1)、 , ;(2)、将三角板的直角顶点F沿方向滑动,同时顶点D沿方向在射线上滑动,如图2.①当点F恰好是线段中点时,求的度数;
②当点F从初始位置滑动到点A处时,请直接写出点E所经过的路径长;
(3)、在(2)的条件下,过点D,F分别作 , 的垂线,两条垂线相交于点P,连接 , 线段的长度是否为定值?如果是,请求出结果;如果不是,请说明理由.36. 如图,在小学我们通过观察、实验的方法得到了“三角形内角和是180°”的结论。小明通过这学期的学习知道:由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的符合题意性.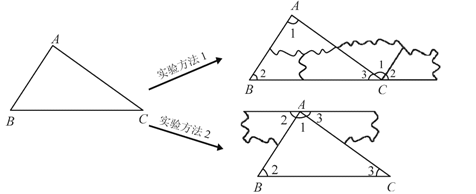
受到实验方法1的启发,小明形成了证明该结论的想法:实验1的拼接方法直观上看,是把和移动到的右侧,且使这三个角的顶点重合,如果把这种拼接方法抽象为几何图形,那么利用平行线的性质就可以解决问题了.
小明的证明过程如下:
已知:如图, . 求证: .

证明:延长 , 过点作 .
∴ ▲ (两直线平行,内错角相等),
( ▲ ).
∵(平角定义),
∴ .
(1)、请你补充完善小明方法1的证明过程;(2)、请你参考小明解决问题的方法1的思路,自行画图标注好顶点字母,写出方法2证明该结论的过程.37. 以下是一个合作学习小组在一次数学实验中的过程记录,请阅读后完成下列问题.(1)、(度量操作)如图1,AB⊥PQ ,垂足为A,AB=3,E为射线AQ上一个动点(点E与点A不重合),∠AEB=∠BEC,BC⊥BE,过点C作CD⊥PQ,垂足为点D.在探究线段AB、线段AE、线段AD三者之间的关系时,通过画图、度量,收集到一组数据如下表:(单位:cm)

AE
1
1.5
1.8
2
2.25
3
4
4.5
5
AD
9
6
5
4.5
4
3
2.25
2
1.8
根据学习函数的经验,选取上表中 和 的数据进行分析:
①设 , ,以 为坐标,在图2所示的坐标系中描出对应的点;
②连线.
(2)、(观察思考)结合表中的数据,猜想:当AB=3时, .
(3)、进一步猜想:AB⊥PQ,垂足为A,E为射线AQ上一个动点(点E与点A不重合),∠AEB=∠BEC,BC⊥BE,过点C作CD⊥PQ,垂足为点D.则线段AB、AE、AD三者之间的关系为.(4)、(推理证明)请利用图1证明上述(4)中的猜想.
(5)、(逆向运用)如图3为一张四边形ABCD纸片,∠BAD=∠ADC=90°, , AD=2,请通过折纸的方法在AD边上找一个点E,使得BE平分∠AEC.(答题要求:简单叙述折纸的方法即可,不需要证明.)

图3
-