备考2024年中考数学核心素养专题七 几何图形的新定义问题
试卷更新日期:2024-03-10 类型:二轮复习
一、选择题
-
1. 如图矩形与正方形的形状有差异,我们将矩形与正方形的接近程度称为矩形的“接近度”,已知矩形ABCD的对角线AC , BD相交于点O , 我们将矩形的“接近度”定义为 , 若∠BOC=60°时,则矩形的“接近度”为( )
 A、 B、3 C、 D、2. 定义:在 , D,E分别是两边的中点,如果上的所有点都在的内部或边上,则称为的中内弧.如图1,是的一条中内弧,如图2,在中, , D,E分别是AB,AC的中点.则所有中内弧所组成的图形(图中阴影部分表示)为( )
A、 B、3 C、 D、2. 定义:在 , D,E分别是两边的中点,如果上的所有点都在的内部或边上,则称为的中内弧.如图1,是的一条中内弧,如图2,在中, , D,E分别是AB,AC的中点.则所有中内弧所组成的图形(图中阴影部分表示)为( ) A、
A、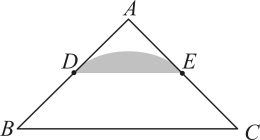 B、
B、 C、
C、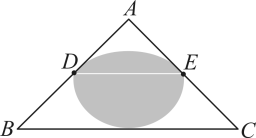 D、
D、 3. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )
3. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )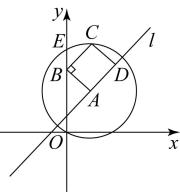 A、12 B、 C、 D、4. 百度百科这样定义凹四边形:把四边形的某边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.关于凹四边形 (如图),以下结论:
A、12 B、 C、 D、4. 百度百科这样定义凹四边形:把四边形的某边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形.关于凹四边形 (如图),以下结论:① ;②若 ,则 ;③若 ,则 ;④存在凹四边形 ,有 .其中所有正确结论的序号是( )
 A、①② B、①②③ C、①②④ D、①③④5. 我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1::2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( )
A、①② B、①②③ C、①②④ D、①③④5. 我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1::2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( ) A、①② B、①③ C、②④ D、③④
A、①② B、①③ C、②④ D、③④二、填空题
-
6. 定义:从一个角的顶点出发,在角的内部引两条射线,如果这两条射线所成的角等于这个角的一半,那么这两条射线所成的角叫做这个角的内半角.已知∠AOB=30°,把一块含有30°角的三角板如图1叠放,将三角板绕顶点O以2度1秒的速度按顺时针方向旋转(如图2).在旋转一周的过程中,射线OA,OB,OC,OD构成内半角,则旋转时间为秒.
 7. 对于平面直角坐标系xOy中的图形M和点P给出如下定义:Q为图形M上任意一点,若P,Q两点间距离的最大值和最小值都存在,且最大值是最小值的5倍,则称点P为图形M的“五分点”.已知点 , .以点O为圆心,r为半径画圆,若线段AB上存在的“五分点”,则r的取值范围是.
7. 对于平面直角坐标系xOy中的图形M和点P给出如下定义:Q为图形M上任意一点,若P,Q两点间距离的最大值和最小值都存在,且最大值是最小值的5倍,则称点P为图形M的“五分点”.已知点 , .以点O为圆心,r为半径画圆,若线段AB上存在的“五分点”,则r的取值范围是. 8. 定义:平面中两条直线 和 相交于点O,对于平面上任意一点M,若p,q分别是M到直线 和 的距离,则称有序非负实数对 是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是.9. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰三角形ABC是“倍长三角形”,底边的长为3,则腰AB的长为.10. 新定义:将一个凸四边形分成一个等腰三角形和一个等腰直角三角形的对角线叫做这个四边形的“等腰直角线”.已知一个直角梯形的“等腰直角线”等于4,它的面积是 .11. 定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC , 那么∠ADC=度12. 定义:以直角三角形的重心为圆心,且与该直角三角形的一边相切的圆叫做这个直角三角形的重切圆.斜边为10,重切圆半径为2的直角三角形的面积是.13. 我们规定菱形与正方形接近程度称为“接近度”,设菱形相邻两个内角的度数分别为 , , 将菱形的“接近度”定义为 , 于是越小,菱形越接近正方形.
8. 定义:平面中两条直线 和 相交于点O,对于平面上任意一点M,若p,q分别是M到直线 和 的距离,则称有序非负实数对 是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是.9. 定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰三角形ABC是“倍长三角形”,底边的长为3,则腰AB的长为.10. 新定义:将一个凸四边形分成一个等腰三角形和一个等腰直角三角形的对角线叫做这个四边形的“等腰直角线”.已知一个直角梯形的“等腰直角线”等于4,它的面积是 .11. 定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC , 那么∠ADC=度12. 定义:以直角三角形的重心为圆心,且与该直角三角形的一边相切的圆叫做这个直角三角形的重切圆.斜边为10,重切圆半径为2的直角三角形的面积是.13. 我们规定菱形与正方形接近程度称为“接近度”,设菱形相邻两个内角的度数分别为 , , 将菱形的“接近度”定义为 , 于是越小,菱形越接近正方形.①若菱形的一个内角为 , 则该菱形的“接近度”为;
②当菱形的“接近度”等于时,菱形是正方形.
 14. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P , 使得△CMP为“智慧三角形”,则点P的坐标为: .
14. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P , 使得△CMP为“智慧三角形”,则点P的坐标为: .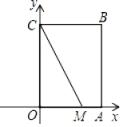 15. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .
15. 定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等弦圆”,现在有一个斜边长为6的等腰直角三角形,当等弦圆最大时,这个圆的半径为 .三、综合题
-
16. 定义:有一组对角之差为90°的四边形为美好四边形.
 (1)、如图①,△ABC中,∠A=2∠C,点D,E分别在AB,AC上,AD=AE,求证:四边形DBCE为美好四边形;(2)、请在图②,图③中分别画一个以AB为边且顶点在格点的美好四边形ABCD;(3)、在(1)的条件下,若DE经过△ABC的内心,BD=4,CE=7,求DE的长.17. 我们定义:连接凸四边形一组对边中点的线段叫做四边形的“准中位线”.
(1)、如图①,△ABC中,∠A=2∠C,点D,E分别在AB,AC上,AD=AE,求证:四边形DBCE为美好四边形;(2)、请在图②,图③中分别画一个以AB为边且顶点在格点的美好四边形ABCD;(3)、在(1)的条件下,若DE经过△ABC的内心,BD=4,CE=7,求DE的长.17. 我们定义:连接凸四边形一组对边中点的线段叫做四边形的“准中位线”. (1)、概念理解:如图1,四边形ABCD中,F为CD的中点,∠ADB=90°,E是AB边上一点,满足DE=AE,试判断EF是否为四边形ABCD的准中位线,并说明理由.(2)、问题探究:如图2,△ABC中,∠ACB=90°,AC=6,BC=8,动点E以每秒1个单位的速度,从点A出发向点C运动,动点F以每秒6个单位的速度,从点C出发沿射线CB运动,当点E运动至点C时,两点同时停止运动.D为线段AB上任意一点,连接并延长CD,射线CD与点A,B,E,F构成的四边形的两边分别相交于点M,N,设运动时间为t.问t为何值时,MN为点A,B,E,F构成的四边形的准中位线.(3)、应用拓展:如图3,EF为四边形ABCD的准中位线,AB=CD,延长FE分别与BA,CD的延长线交于点M,N,请找出图中与∠M相等的角并证明.18. 定义:有两个相邻内角和等于另两个内角和的一半的四边形称为对半四边形,这两个角的夹边称为对半线.
(1)、概念理解:如图1,四边形ABCD中,F为CD的中点,∠ADB=90°,E是AB边上一点,满足DE=AE,试判断EF是否为四边形ABCD的准中位线,并说明理由.(2)、问题探究:如图2,△ABC中,∠ACB=90°,AC=6,BC=8,动点E以每秒1个单位的速度,从点A出发向点C运动,动点F以每秒6个单位的速度,从点C出发沿射线CB运动,当点E运动至点C时,两点同时停止运动.D为线段AB上任意一点,连接并延长CD,射线CD与点A,B,E,F构成的四边形的两边分别相交于点M,N,设运动时间为t.问t为何值时,MN为点A,B,E,F构成的四边形的准中位线.(3)、应用拓展:如图3,EF为四边形ABCD的准中位线,AB=CD,延长FE分别与BA,CD的延长线交于点M,N,请找出图中与∠M相等的角并证明.18. 定义:有两个相邻内角和等于另两个内角和的一半的四边形称为对半四边形,这两个角的夹边称为对半线.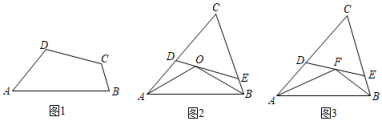 (1)、如图1,在对半四边形ABCD中,∠A+∠B=(∠C+∠D),求∠A与∠B的度数之和;(2)、如图2,O为锐角△ABC的外心,过点O的直线交AC,BC于点D,E,∠OAB=30°,求证:四边形ABED是对半四边形;(3)、如图3,在△ABC中,D,E分别是AC,BC上一点,CD=CE=3,CE=3EB,F为DE的中点,∠AFB=120°,当AB为对半四边形ABED的对半线时,求AC的长.19. 定义:若圆内接三角形是等腰三角形,我们就称这样的三角形为“圆等三角形”.
(1)、如图1,在对半四边形ABCD中,∠A+∠B=(∠C+∠D),求∠A与∠B的度数之和;(2)、如图2,O为锐角△ABC的外心,过点O的直线交AC,BC于点D,E,∠OAB=30°,求证:四边形ABED是对半四边形;(3)、如图3,在△ABC中,D,E分别是AC,BC上一点,CD=CE=3,CE=3EB,F为DE的中点,∠AFB=120°,当AB为对半四边形ABED的对半线时,求AC的长.19. 定义:若圆内接三角形是等腰三角形,我们就称这样的三角形为“圆等三角形”. (1)、如图1,AB是⊙O的一条弦(非直径),若⊙O在上找一点C,使得△ABC是“圆等三角形”,则这样的点C能找到个.(2)、如图2,四边形ABCD是⊙O的内接四边形,连结对角线BD,△ABD和△BCD均为“圆等三角形”,且AB=AD.
(1)、如图1,AB是⊙O的一条弦(非直径),若⊙O在上找一点C,使得△ABC是“圆等三角形”,则这样的点C能找到个.(2)、如图2,四边形ABCD是⊙O的内接四边形,连结对角线BD,△ABD和△BCD均为“圆等三角形”,且AB=AD.①当∠A=140°时,求∠ADC的度数;
②如图3,当∠A=120°,AB=6时,求阴影部分的面积.
20. 综合与实践新定义:我们把两个面积相等但不全等的三角形叫做积等三角形.
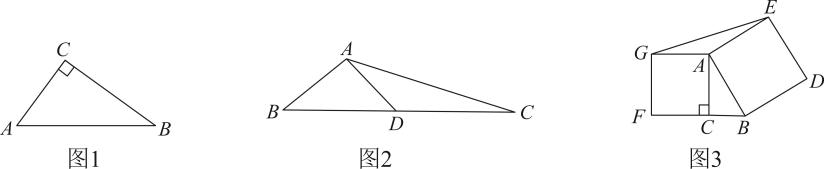 (1)、【初步尝试】如图1,已知中, , , , P为上一点,当AP=时,与为积等三角形;(2)、【理解运用】如图2,与为积等三角形;若 , , 且线段的长度为正整数,求的长;(3)、【综合应用】如图3,已知中, , 分别以 , 为边向外作正方形和正方形 , 连接 , 求证:与为积等三角形.21. 定义:有一组对角互补的四边形叫做“对补四边形”,例如,四边形 中,若 或 ,则四边形 是“对补四边形”.
(1)、【初步尝试】如图1,已知中, , , , P为上一点,当AP=时,与为积等三角形;(2)、【理解运用】如图2,与为积等三角形;若 , , 且线段的长度为正整数,求的长;(3)、【综合应用】如图3,已知中, , 分别以 , 为边向外作正方形和正方形 , 连接 , 求证:与为积等三角形.21. 定义:有一组对角互补的四边形叫做“对补四边形”,例如,四边形 中,若 或 ,则四边形 是“对补四边形”.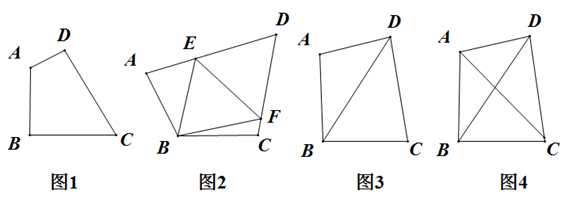 (1)、(概念理解)
(1)、(概念理解)
如图1,四边形 是“对补四边形”.①若 ,则 ;
②若 .且 时.则 ;
(2)、(拓展提升)
如图,四边形 是“对补四边形”,当 ,且 时,图中 之间的数量关系是 , 并证明这种关系;(3)、(类比应用)
如图3,在四边形 中, 平分 ;①求证:四边形 是“对补四边形”;
②如图4,连接 ,当 ,且 时,求 的值.
22. 定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.根据以上定义,解决下列问题:
 (1)、判断正方形“直等补”四边形;菱形“直等补”四边形.(填“是”或“不是”)(2)、如图1,在所给的网格中,画出符合条件的“直等补”四边形AECF;(3)、如图2,已知四边形ABCD是“直等补”四边形,AB=BC=5,CD=1,AD>AB,点B到直线AD的距离为BE.
(1)、判断正方形“直等补”四边形;菱形“直等补”四边形.(填“是”或“不是”)(2)、如图1,在所给的网格中,画出符合条件的“直等补”四边形AECF;(3)、如图2,已知四边形ABCD是“直等补”四边形,AB=BC=5,CD=1,AD>AB,点B到直线AD的距离为BE.①求BE的长;
②若M、N分别是AB、AD边上的动点,求△MNC周长的最小值.
23. 在平面直角坐标系中,对于线段AB与直线 , 给出如下定义:若线段AB关于直线l的对称线段为( , 分别为点A,B的对应点),则称线段为线段AB的“关联线段”.已知点 , .
(1)、线段为线段AB的“关联线段”,点的坐标为 , 则的长为 , b的值为;(2)、线段为线段AB的“关联线段”,直线经过点 , 若点 , 都在直线上,连接 , 求的度数;(3)、点 , , 线段为线段AB的“关联线段”,且当b取某个值时,一定存在k使得线段与线段PQ有公共点,直接写出b的取值范围.24. 新定义:垂直于图形的一边且等分这个图形面积的直线叫作图形的等积垂分线,等积垂分线被该图形截的线段叫做等积垂分线段.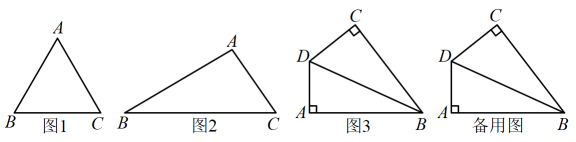
问题探究:
(1)、如图1,等边边长为3,垂直于边的等积垂分线段长度为;(2)、如图2,在中, , , , 求垂直于边的等积垂分线段长度;(3)、如图3,在四边形中, , , , 求出它的等积垂分线段长.25. 在平面直角坐标系中,给出如下定义:为图形上任意一点,如果点到直线的距离等于图形上任意两点距离的最大值时,那么点称为直线的“伴随点”.例如:如图1,已知点 , , 在线段上,则点是直线:轴的“伴随点”.
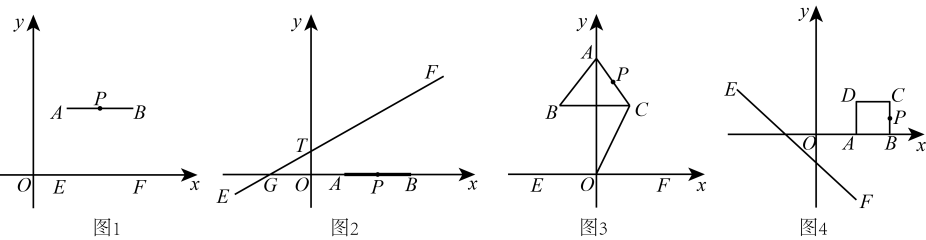 (1)、如图2,已知点 , , 是线段上一点,直线过 , 两点,当点是直线的“伴随点”时,求点的坐标;(2)、如图3,轴上方有一等边三角形 , 轴,顶点在轴上且在上方, , 点是上一点,且点是直线:轴的伴随点 . 当点到轴的距离最小时,求等边三角形的边长;(3)、如图4,以 , , 为顶点的正方形上始终存在点 , 使得点是直线:的伴随点 . 请直接写出的取值范围.26. 定义:对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的四边形,则这样的四边形称为镶嵌四边形.
(1)、如图2,已知点 , , 是线段上一点,直线过 , 两点,当点是直线的“伴随点”时,求点的坐标;(2)、如图3,轴上方有一等边三角形 , 轴,顶点在轴上且在上方, , 点是上一点,且点是直线:轴的伴随点 . 当点到轴的距离最小时,求等边三角形的边长;(3)、如图4,以 , , 为顶点的正方形上始终存在点 , 使得点是直线:的伴随点 . 请直接写出的取值范围.26. 定义:对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的四边形,则这样的四边形称为镶嵌四边形. (1)、如图1,将纸片沿中位线折叠,使点落在边上的处,再将纸片分别沿 , 折叠,使点和点都与点重合,得到双层四边形 , 则双层四边形为形.(2)、纸片按图2的方式折叠,折成双层四边形为矩形,若 , , 求的长.(3)、如图3,四边形纸片满足 , , , , . 把该纸片折叠,得到双层四边形为正方形.请你画出一种折叠的示意图,并直接写出此时的长.27. 定义:由一个三角形的三条中线围成的三角形称为原三角形的中线三角形.
(1)、如图1,将纸片沿中位线折叠,使点落在边上的处,再将纸片分别沿 , 折叠,使点和点都与点重合,得到双层四边形 , 则双层四边形为形.(2)、纸片按图2的方式折叠,折成双层四边形为矩形,若 , , 求的长.(3)、如图3,四边形纸片满足 , , , , . 把该纸片折叠,得到双层四边形为正方形.请你画出一种折叠的示意图,并直接写出此时的长.27. 定义:由一个三角形的三条中线围成的三角形称为原三角形的中线三角形.问题:设中线三角形的面积为 , 原三角形的面积为.求的值.

特例探索:
(1)、正三角形的边长为2,则中线长为 , 所以.(2)、如图1,每个小正方形边长均为1,点均在网格点上.①的中线三角形.(填“是”或“不是”)
② , , 所以.
(3)、一般情形:如图2,的三条中线分别是 , 将平移至 , 连接.
求证:是的中线三角形;(4)、猜想的值,并说明理由.28. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是一次函数图像的“1阶方点”. (1)、在① , ② , ③三点中,是反比例函数图像的“2阶方点”的有(填序号);(2)、如图,已知抛物线交y轴于点C,一次函数的图像交抛物线第二象限于点P,点Q为该一次函数图象的“1阶方点”.
(1)、在① , ② , ③三点中,是反比例函数图像的“2阶方点”的有(填序号);(2)、如图,已知抛物线交y轴于点C,一次函数的图像交抛物线第二象限于点P,点Q为该一次函数图象的“1阶方点”.①求的面积的最大值;
②若一次函数图像的“1阶方点”有且只有一个,求a的值;
(3)、若抛物线的“m阶方点”一定存在,求m的取值范围.29. 我们定义:对角线垂直的凸四边形叫做“准筝形”如图1,四边形中, , 则四边形是“准筝形”.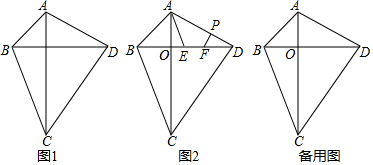 (1)、“三条边相等的准筝形是菱形”是命题;(填“真”或“假”)(2)、如图1,在准筝形中, , , , 求的长.(3)、如图2,在准筝形中,与交于点 , 点在线段上, , 且 , , 在上存在移动的线段 , 在的左侧,且 , 使四边形周长最小,求此时的长度.30. 定义:长宽比为 :1(n为正整数)的矩形称为 矩形.
(1)、“三条边相等的准筝形是菱形”是命题;(填“真”或“假”)(2)、如图1,在准筝形中, , , , 求的长.(3)、如图2,在准筝形中,与交于点 , 点在线段上, , 且 , , 在上存在移动的线段 , 在的左侧,且 , 使四边形周长最小,求此时的长度.30. 定义:长宽比为 :1(n为正整数)的矩形称为 矩形.下面,我们通过折叠的方式折出一个 矩形,如图a所示.
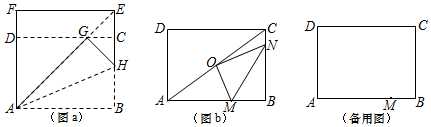
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为 矩形.
(1)、证明:四边形ABCD为 矩形;(2)、点M是边AB上一动点.①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求 的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2 ,则DR的最小值= ▲ .
31. 综合与实践定义:将宽与长的比值为(为正整数)的矩形称为阶奇妙矩形.
(1)、概念理解:当时,这个矩形为1阶奇妙矩形,如图(1),这就是我们学习过的黄金矩形,它的宽()与长的比值是 .
(2)、操作验证:用正方形纸片进行如下操作(如图(2)):
第一步:对折正方形纸片,展开,折痕为 , 连接;
第二步:折叠纸片使落在上,点的对应点为点 , 展开,折痕为;
第三步:过点折叠纸片,使得点分别落在边上,展开,折痕为 .
试说明:矩形是1阶奇妙矩形.
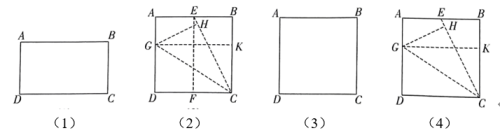 (3)、方法迁移:
(3)、方法迁移:用正方形纸片折叠出一个2阶奇妙矩形.要求:在图(3)中画出折叠示意图并作简要标注.
(4)、探究发现:小明操作发现任一个阶奇妙矩形都可以通过折纸得到.他还发现:如图(4),点为正方形边上(不与端点重合)任意一点,连接 , 继续(2)中操作的第二步、第三步,四边形的周长与矩形的周长比值总是定值.请写出这个定值,并说明理由.