备考2024年中考数学核心素养专题六数与式的新定义问题

试卷更新日期：2024-03-10 类型：二轮复习

进入出卷网下载

一、选择题

1. 定义一种新运算： $a$ ※ $b = b^{2} - a b$ ，则 $(- 2)$ ※ $(- 1)$ 的是（）．

A、－1 B、1 C、3 D、2

查看试题解析
2. 定义：给定关于x的函数 y ，对于该函数图象上任意两点（x₁ ， y₁），（x₂ ， y₂），当x₁﹤x₂时，都有y₁﹤y₂ ，称该函数为增函数.根据以上定义，下列函数中①y=2x；② $y = - x + 1$ ；③ $y = x_{}^{2} (x > 0)$ ；④ $m x^{2} - (m - 1) x - 1 = 0$ ，是增函数的（）

A、①③④ B、①② C、③④ D、①③

查看试题解析
3. 对于整数n，定义 $[\sqrt{n}]$ 为不大于 $\sqrt{n}$ 的最大整数，例如： $[\sqrt{2}] = 1$ ， $[\sqrt{6}] = 2$ ， $[\sqrt{9}] = 3$ .对26进行如下操作： $26 \begin{array}{l} \underset{\to}{第一次} \end{array} [\sqrt{26}] = 5 \begin{array}{l} \underset{\to}{第二次} \end{array} [\sqrt{5}] = 2$ ，即对26进行2次操作后变为2.若对整数a进行2次操作后变为3，则a的最大值为（）

A、256 B、255 C、81 D、80

查看试题解析
4. 定义一种运算： $a * b = {\begin{array}{l} a ， a \geq b \\ b ， a < b \end{array}$ ，则不等式 $(2 x + 1) * (2 - x) > 3$ 的解集是（）

A、 $x > 1$ 或 $x < \frac{1}{3}$ B、 $- 1 < x < \frac{1}{3}$ C、 $x > 1$ 或 $x < - 1$ D、 $x > \frac{1}{3}$ 或 $x < - 1$

查看试题解析
5. 定义新运算： $m \oplus n = - \frac{n}{m} (m \neq 0)$ ，则对于函数 $y = x \oplus 2$ ，下列说法正确的是（）

A、当 $x < 0$ 时， $y$ 随 $x$ 增大而增大 B、该函数图象经过点 $(2 ， 1)$ C、该函数图象位于第一、三象限 D、当 $- 2 < x < - 1$ 时， $- 2 < y < - 1$

查看试题解析
6. 定义新运算： $p \oplus q = {\begin{array}{l} \frac{p}{q} (q > 0) ， \\ - \frac{p}{q} (q < 0) ， \end{array}$ 例如 $3 \oplus 5 =$ $\frac{3}{5} ， 3 \oplus (- 5) = \frac{3}{5}$ ，则 $y = 2 \oplus x (x \neq 0)$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析
7. 在数的学习过程中，我们总会对其中一些具有某种特性的数充满好奇，如学习自然数时，我们发现一种特殊的自然数——“好数”.定义：对于三位自然数n，各位数字都不为0，且百位数字与十位数字之和恰好能被个位数字整除，则称这个自然数n为“好数”.例如：426是“好数”，因为4，2，6都不为0，且 $4 + 2 = 6$ ， 6能被6整除；643不是“好数”，因为 $6 + 4 = 10$ ， 10不能被3整除.则百位数字比十位数字大5的所有“好数”的个数是（）

A、8 B、7 C、6 D、5

查看试题解析
8. 定义 $\min (a ， b)$ ，当 $a \geq b$ 时， $\min (a ， b) = b$ ，当 $a$ ＜ $b$ 时， $\min (a ， b) = a$ ；已知函数 $y = \min (- x - 3 ， 2 x - 21)$ ，则该函数的最大值是（）

A、-15 B、-9 C、-6 D、6

查看试题解析
9. 定义：如果代数式 $A = a_{1} x^{2} + b_{1} x + c_{1}$ ( $a_{1} \neq 0$ ， $a_{1}$ ， $b_{1}$ ， $c_{1}$ 是常数)与 $B = a_{2} x^{2} + b_{2} x + c_{2}$ ( $a_{2} \neq 0$ ， $a_{2}$ ， $b_{2}$ ， $c_{2}$ 是常数)，满足 $a_{1} + a_{2} = 0$ ， $b_{1} + b_{2} = 0$ ， $c_{1} + c_{2} = 0$ ，则称这两个代数式 $A$ 与 $B$ 互为“和谐式”，对于上述“和谐式” $A$ 、 $B$ ，下列三个结论正确的个数为（）
①若 $A = - x^{2} - \frac{4}{3} m x - 2$ ， $B = x^{2} - 2 n x + n$ ，则 $(m + n)^{2023}$ 的值为-1；
②若 $k$ 为常数，关于 $x$ 的方程 $A = k$ 与 $B = k$ 的解相同，则 $k = 0$ ；
③若 $p$ ， $q$ 为常数， $p A + q B$ 的最小值为 $p - q$ ，则 $A$ 有最小值，且最小值为1.

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 我们定义一种新函数：形如 $y = | a x^{2} + b x + c | (a \neq 0 ， b^{2} - 4 a c > 0)$ 的函数叫做“鹊桥”函数 $.$ 数学兴趣小组画出一个“鹊桥”函数 $y = | x^{2} + b x + c |$ 的图象如图所示，则下列结论正确的是（）

A、 $b c < 0$ B、 $c = 3$ C、当直线 $y = x + m$ 与该图像恰有三个公共点时，则 $m = 1$ D、关于 $x$ 的方程 $| x^{2} + b x + c | = 3$ 的所有实数根的和为 $4$

查看试题解析

二、填空题

11. 对于实数a，b，定义运算“◎”如下：
a◎b＝（a+b）²-（a-b）² ．若（m+1）◎（m-2）＝16，

则m＝．

查看试题解析
12. 定义：如果一个正整数能表示为两个正整数m，n的平方差，且 $m - n > 1$ ，则称这个正整数为“智慧优数”.例如， $16 = 5^{2}$ $- 3^{2} ， 16$ 就是一个智慧优数，可以利用 $m^{2} -$ $n^{2} = (m + n) (m - n)$ 进行研究.若将智慧优数从小到大排列，则第3个智慧优数是；第23个智慧优数是.

查看试题解析
13. 对于任意非零实数a、b，定义一种新运算“*”如下：a*b= $\frac{a - b}{2 a b}$ ，则1*2+ 2*3+3*4+……+2020*2021= ．

查看试题解析
14. 定义一种新运算：对于任意的非零实数a，b，a $\otimes$ b= $\frac{1}{a} + \frac{1}{b}$ ．若(x+1) $\otimes$ x= $\frac{2 x + 1}{x}$ ，则x的值为

查看试题解析
15. 若定义一种新运算： $m @ n = \{\begin{array}{l} m - n (m \leq n) \\ m + n - 3 (m > n) \end{array}$ ，例如： $1$ @ $2 = 1 - 2 = - 1$ ， $4$ @ $3 = 4 + 3 - 3 = 4 .$ 下列说法：

(1)、 $- 7$ @ $9 =$ ；

(2)、 $y = (- x + 1)$ @ $(x^{2} - 2 x + 1)$ 与直线 $y = m (m$ 为常数 $)$ 有 $1$ 个交点，则 $m$ 的取值范围是．

查看试题解析
16. 定义：若一个函数图象上存在横纵坐标相等的点，则称该点为这个函数图象的“等值点”．例如，点 $(- 1 ， - 1)$ 是函数 $y = 2 x + 1$ 的图象的“等值点”．若函数 $y = x^{2} - 2 (x \geq m)$ 的图象记为 $W_{1}$ ，将其沿直线 $x = m$ 翻折后的图象记为 $W_{2}$ ．当 $W_{1}$ 、 $W_{2}$ 两部分组成的图象上恰有2个“等值点”时， $m$ 的取值范围为．

查看试题解析

三、解答题

17. 在实数范围内定义新运算“ $△$ ”，其规则为： $a △ b = a^{2} - a b$ ，根据这个规则，解决下列问题：

(1)、求 $(x + 2) △ 5 = 0$ 中的x值；

(2)、证明： $(x + m) △ 5 = 0$ 中，无论m为何值，x总有两个不同的值.

查看试题解析
18. 定义一种新运算： $x * y = x - x \div y$ ，如 $(- 3) * (- 5) = - 3 - (- 3) \div (- 5) = - 3 \frac{3}{5}$ ，按照上述定义计算 $[9 * (- 1)] * (- 2)$ 的值.

查看试题解析
19. 定义：若两个二次根式a ， b满足 $a \cdot b = c$ ，且c是有理数，则称a与b是关于c的共轭二次根式．

(1)、若a与 $\sqrt{2}$ 是关于4的共轭二次根式，则a=

(2)、若 $3 + \sqrt{3}$ 与 $6 + \sqrt{3} m$ 是关于12的共轭二次根式，求m的值．

查看试题解析
20. 请你根据王老师所给的内容（如表），完成下列各小题．
我们定义一个关于非零常数a，b的新运算，规定：a〇b＝ax+by．例如：3〇2＝3x+2y．

(1)、如果x＝5，2〇4＝-18，求y的值；

(2)、若1〇1＝8，4〇2＝20，求x，y的值．

查看试题解析
21. 对于数轴上不重合的两点A ， B ，给出如下定义：若数轴上存在一点M ，通过比较线段AM和BM的长度，将较短线段的长度定义为点M到线段AB的“绝对距离”．若线段AM和BM的长度相等，将线段AM或BM的长度定义为点M到线段AB的“绝对距离”．

(1)、当数轴上原点为O ，点A表示的数为-1，点B表示的数为5时
①点O到线段AB的“绝对距离”为；
②点M表示的数为m ，若点M到线段AB的“绝对距离”为3，则m的值为；

(2)、在数轴上，点P表示的数为-6，点A表示的数为-3，点B表示的数为2．点P以每秒2个单位长度的速度向正半轴方向移动时，点B同时以每秒1个单位长度的速度向负半轴方向移动，设移动的时间为 $t (t > 0)$ 秒，当点P到线段AB的“绝对距离”为2时，求t的值．

查看试题解析
22. 对于平面直角坐标系 $x O y$ 中的点 $P (a ， b) (b = 0)$ ，给出如下定义：当 $a ⩾ b$ 时， $k = | \frac{b}{a} |$ ；当 $a < b$ 时 $k = | \frac{a}{b} |$ ， k叫做点P的“斜值”．

(1)、直接写出点 $P (- 3 ， \sqrt{3})$ 的“斜值”k的值；

(2)、若点 $P (a ， b)$ 的“斜值” $k = \frac{1}{2}$ ，且 $b - a = 2$ ，求点P的坐标；

(3)、如图，正方形 $A B C D$ 中， $A (m ， 1)$ ， $B (m ， - 1)$ ， $C (m + 2 ， - 1)$ ，若正方形 $A B C D$ 的边上存在两个点的“斜值”为 $\frac{1}{2}$ ，直接写出m的取值范围．

查看试题解析
23. 定义：在平面直角坐标系 $x O y$ 中，当点 $N$ 在图形 $M$ 的内部，或在图形 $M$ 上，且点 $N$ 的横坐标和纵坐标相等时，则称点 $N$ 为图形 $M$ 的“和谐点”．

(1)、如图，矩形 $A B C D$ 的顶点坐标分别是 $A (- 1，2)$ ， $B (- 1 ， - 1)$ ， $C (3 ， - 1)$ ， $D (3，2)$ ，在点 $M_{1} (1，1)$ ， $M_{2} (2，2)$ ， $M_{3} (3，3)$ 中，是矩形 $A B C D$ “和谐点”的是；

(2)、点 $G (2，2)$ 是反比例函数 $y_{1} = \frac{k}{x}$ 图象上的一个“和谐点”，则该函数图象上的另一个“和谐点” $H$ 的坐标是，直线 $G H$ 的表达式是 $y_{2} =$ ；

(3)、已知点 $A$ ， $B$ 是抛物线 $y = - \frac{1}{2} {(x - 1)}^{2} + 5$ 上的“和谐点”，点 $A$ 在点 $B$ 的左侧，点 $C$ 是抛物线的顶点，连接 $A C$ ， $A B$ ， $B C$ ，求点 $A$ ， $B$ 的坐标，并直接写出 $∆ A B C$ 的面积．

查看试题解析
24. 若定义：若一个函数图象上存在纵坐标是横坐标2倍的点，则把该函数称为“明德函数”，该点称为“明德点”，例如：“明德函数” $y = x + 1$ ，其“明德点”为 $(1 ， 2)$ .

(1)、①判断：函数 $y = 2 x + 3$ “明德函数”（填“是”或“不是”）；
②函数 $y = x^{2}$ 的图像上的明德点是；

(2)、若抛物线 $y = (m - 1) x^{2} + m x + \frac{1}{4} m$ 上有两个“明德点”，求 $m$ 的取值范围；

(3)、若函数 $y = x^{2} + (m - k + 2) x + \frac{n}{4} - \frac{1}{2} k$ 的图象上存在唯一的一个“明德点”，且当 $- 1 \leq m \leq 3$ 时， $n$ 的最小值为 $k$ ，求 $k$ 的值.

查看试题解析
25. 对于正数 $x$ ，用符号 $[x]$ 表示 $x$ 的整数部分，例如 $[0.1] = 0$ ， $[2.5] = 2$ ， $[3] = 3 .$ 点 $A (a ， b)$ 在第一象限内，以 $A$ 为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直 $.$ 其中垂直于 $y$ 轴的边长为 $a$ ，垂直于 $x$ 轴的边长为 $[b] + 1$ ，那么，把这个矩形覆盖的区域叫做点 $A$ 的矩形域 $.$ 例如：点 $(3 ， \frac{3}{2})$ 的矩形域是一个以 $(3 ， \frac{3}{2})$ 为对角线交点，长为 $3$ ，宽为 $2$ 的矩形所覆盖的区域，如图 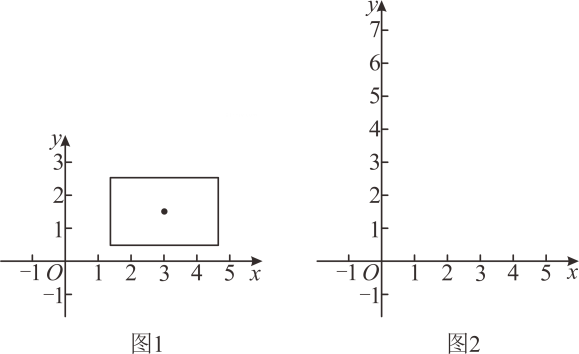$1$ 所示，它的面积是 $6$ ．
根据上面的定义，回答下列问题：

(1)、在图 $2$ 所示的坐标系中画出点 $(2 ， \frac{7}{2})$ 的矩形域，该矩形域的面积是；

(2)、点 $P (2 ， \frac{7}{2})$ ， $Q (a ， \frac{7}{2}) (a > 0)$ 的矩形域重叠部分面积为 $1$ ，则 $a$ 的值为．

查看试题解析
26. 【定义】在平面直角坐标系xOy中，对于点 $P (a ， b)$ 和点 $Q (a ， b^{'})$ ，给出如下定义：若 $b^{'} = {\begin{array}{l} b (a \geq 1) \\ - b (a < 1) \end{array}$ ，则称点Q为点P的限变点，例如：点 $(2 ， 4)$ 的限变点的坐标是 $(2 ， 4)$ ，点 $(- 2 ， 5)$ 的限变点的坐标是 $(- 2 ， - 5)$ ．
【应用】

(1)、①点 $(\sqrt{2} ， 1)$ 的限变点的坐标是；
②以下三个选项中的点是反比例函数 $y = \frac{2}{x}$ 图象上某一个点的限变点的是（）

A． $(- 1 ， - 2)$ B． $(- 1 ， 2)$ C． $(1 ， - 2)$

(2)、若点P在一次函数 $y = - x + 3 (- 2 \leq x \leq 6)$ 的图象上，请在下图平面直角坐标系中，画出点P的限变点Q的函数图象，并根据图象直接写出点Q的纵坐标 $b^{'}$ 的取值范围为．

(3)、【拓展】
我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休”．若点P在关于x的二次函数 $y = {(x - t)}^{2} + t$ 的图象上，其限变点Q的纵坐标 $b^{'}$ 的取值范围是 $b^{'} \geq m$ 或 $b^{'} < n$ ，其中 $m > n$ ，令 $s = m - n$ ，求s关于t的函数解析式．

查看试题解析
27. 定义：由两条与x轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”。

(1)、【概念理解】抛物线 $y = x^{2} - x - 2$ 与抛物线 $y = 2 x^{2} - 2 x - 4$ （填“能”或“不能”)围成“月牙线”.

(2)、【尝试应用】如图，抛物线C₁与抛物线C₂组成一个开口向上的“月牙线”，抛物线C₁与抛物线C₂与x轴有相同的交点M，N（点M在点N的左侧），与y轴的交点分别为A，B，抛物线C₁的解析式为 $y = \frac{1}{4} x^{2} + x + c$ ，抛物线C₂的解析式为 $y = x^{2} + 4 x - 12$ .
①求MN的长和c的值；
②将抛物线C₁与抛物线C₂所围成的“月牙线”向左或向右平移，平移后的“月牙线”与x轴的交点记为M₁ ， N₁ ，与y轴的交点记为A₁ ， B₁ ，当A₁B₁=M₁N₁时，求平移的方向及相应的距离。

查看试题解析
28. 定义：关于x轴对称且对称轴相同的两条抛物线叫作“同轴对称抛物线”．
例如： $y = {(x - 1)}^{2} - 2$ 的“同轴对称抛物线”为 $y = - {(x - 1)}^{2} + 2$ ．

(1)、抛物线 $y = - \frac{1}{2} {(x - 1)}^{2} + \frac{3}{2}$ 的顶点坐标为，它的“同轴对称抛物线”为；

(2)、如图，在平面直角坐标系中，第四象限的点B是抛物线 $y = a x^{2} - 4 a x + 1$ 上一点，点B的横坐标为1，过点B作x轴的垂线，交抛物线 $y = a x^{2} - 4 a x + 1$ 的“同轴对称抛物线”于点C，分别作点B、C关于抛物线 $y = a x^{2} - 4 a x + 1$ 的对称轴对称的点 $B^{'}$ 、 $C^{'}$ ，连接BC、 $C C^{'}$ 、 $C^{'} B^{'}$ 、 $B^{'} B$ ．当四边形 $B C C^{'} B^{'}$ 为正方形时，求a的值．

查看试题解析
29. 定义：在平面直角坐标系xOy中，对于 $⊙ M$ 内的一点P ，若在 $⊙ M$ 外存在点 $P^{'}$ ，使得 $M P^{'} = 2 M P$ ，则称点P为 $⊙ M$ 的“内二分点”.

(1)、当 $⊙ O$ 的半径为2时，
①在 $P_{1} (- 1 ， 0)$ ， $P_{2} (1 ， \frac{3}{2})$ ， $P_{3} (\sqrt{2} ， - 1)$ ， $P_{4} (- \sqrt{3} ， - 1)$ 四个点中，是 $⊙ O$ 的“内二分点”的是 ▲ ；
②已知一次函数 $y = k x - 2 k$ 在第一象限的图象上的所有点都是 $⊙ O$ 的“内二分点”，求k的取值范围；

(2)、已知点 $M (m ， 0)$ ， $B (0 ， - 1)$ ， $C (1 ， - 1)$ ， $⊙ M$ 的半径为4，若线段BC上存在 $⊙ M$ 的“内二分点”，直接写出m的取值范围.

查看试题解析
30. 新定义：已知y是x的函数，若函数图象上存在一点P（a，a+2），则称点P为函数图象上的“朴实点”．例如：直线y＝2x+1上存在的“朴实点”是P（1，3）．

(1)、判断直线y＝ $\frac{1}{3}$ x+4上是否有“朴实点”？若有，直接写出其坐标；若没有，请说明理由；

(2)、若抛物线y＝x²+3x+2-k上存在两个“朴实点”，两个“朴实点”之间的距离为2 $\sqrt{2}$ ，求k的值；

(3)、若二次函数y＝ $\frac{1}{8}$ x²+（m-t+1）x+2n+2t-2的图象上存在唯一的“朴实点”，且当-2≤m≤3时，n的最小值为t+4，求t的值．

查看试题解析

备考2024年中考数学核心素养专题六 数与式的新定义问题

一、选择题

二、填空题

三、解答题

备考2024年中考数学核心素养专题六数与式的新定义问题