初中数学同步训练必刷培优卷(北师大版七年级下册 第二单元测试卷)
试卷更新日期:2024-03-09 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,已知直线EF⊥MN垂足为F,且∠1=125°,若要使AB∥CD,则∠2应等于( )
 A、55° B、45° C、35° D、65°2. 根据投影屏上出示的填空题,判断下列说法正确的是 ( )
A、55° B、45° C、35° D、65°2. 根据投影屏上出示的填空题,判断下列说法正确的是 ( )已知:如图是△ABC.
试说明:∠BAC+∠B+∠C=180°.
解:过点A作DE∥ ◎ .
∴∠DAB=∠B,∠EAC= @ .
又∵∠DAB+∠BAC+∠EAC= ▲ .
∴ ※ +∠BAC+∠C=180°.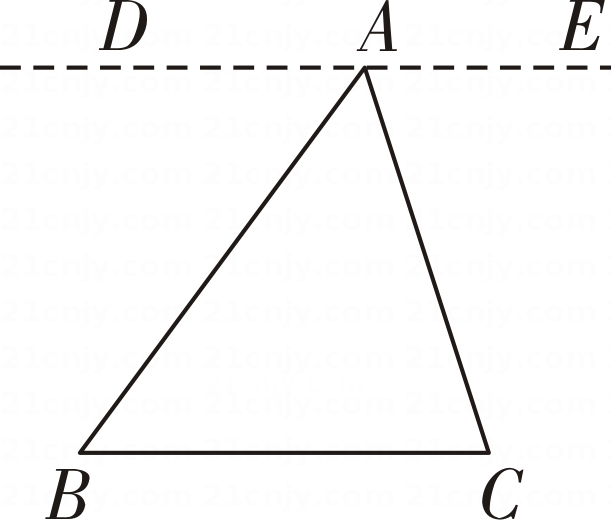 A、◎代表 AB B、@代表∠BAC C、▲代表 90° D、※代表∠B3. 同一平面内五条直线l1 , l2 , l3 , l4与l5的位置关系如图所示,根据图中标示的角度,下列判断正确的是( )
A、◎代表 AB B、@代表∠BAC C、▲代表 90° D、※代表∠B3. 同一平面内五条直线l1 , l2 , l3 , l4与l5的位置关系如图所示,根据图中标示的角度,下列判断正确的是( ) A、l1∥l3 , l2∥l3 B、l2∥l3 , l4与l5相交 C、l1与l3相交,l4∥l5 D、l1与l2相交,l1∥l34. 如图,给出下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°.其中能判定直线l1∥l2的有( )
A、l1∥l3 , l2∥l3 B、l2∥l3 , l4与l5相交 C、l1与l3相交,l4∥l5 D、l1与l2相交,l1∥l34. 如图,给出下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°.其中能判定直线l1∥l2的有( ) A、1个 B、2个 C、3个 D、4个5. 将一副三角板如图放置,则下列结论中,正确的是( )
A、1个 B、2个 C、3个 D、4个5. 将一副三角板如图放置,则下列结论中,正确的是( )①;②如果 , 则有;③如果 , 则有;④如果 , 则有 .
 A、①②③④ B、③④ C、①②④ D、①②③6. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A、①②③④ B、③④ C、①②④ D、①②③6. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )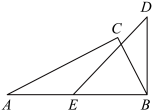 A、或或 B、或或 C、或或 D、或或7. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )
A、或或 B、或或 C、或或 D、或或7. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )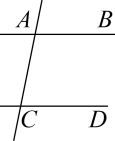 A、③④ B、①③④ C、①②④ D、②③④8. 已知 , 点E在连线的右侧,与的角平分线相交于点F,则下列说法正确的是( );
A、③④ B、①③④ C、①②④ D、②③④8. 已知 , 点E在连线的右侧,与的角平分线相交于点F,则下列说法正确的是( );①;
②若 , 则;
③如图(2)中,若 , , 则;
④如图(2)中,若 , , 则.
 A、①②④ B、②③④ C、①②③ D、①②③④9. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )
A、①②④ B、②③④ C、①②③ D、①②③④9. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )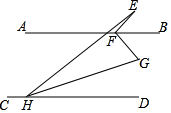 A、90° B、95° C、100° D、150°10. 如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An等于( )
A、90° B、95° C、100° D、150°10. 如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An等于( )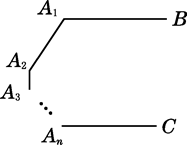 A、180°n B、(n+1)·180° C、(n-1)·180° D、(n-2)·180°
A、180°n B、(n+1)·180° C、(n-1)·180° D、(n-2)·180°二、填空题(每题3分,共15分)
-
11. 如图,同位角有a对,内错角有b对,同旁内角有c对,则a+b+c的值是 .
 12. 一大门的栏杆如图,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
12. 一大门的栏杆如图,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= . 13. 如图,将长方形纸片 ABCD沿EF折叠后,点A,B分别落在A',B'的位置,再沿AD边将∠A'折叠到∠H处,若∠1=52°,则∠AEF= , ∠FEH= .
13. 如图,将长方形纸片 ABCD沿EF折叠后,点A,B分别落在A',B'的位置,再沿AD边将∠A'折叠到∠H处,若∠1=52°,则∠AEF= , ∠FEH= .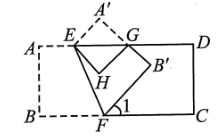 14. 如图,已知直线被直线所截, , 点是平面内位于直线右侧的一动点(点不在直线上),设 , 在点运动过程中,的度数可能是 . (结果用含的式子表示)
14. 如图,已知直线被直线所截, , 点是平面内位于直线右侧的一动点(点不在直线上),设 , 在点运动过程中,的度数可能是 . (结果用含的式子表示)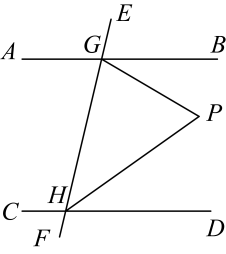 15. 如图,于点 , 于点 , 平分交于点 , 为线段延长线上一点,.给出下列结论:①;②;③.其中结论正确的序号有
15. 如图,于点 , 于点 , 平分交于点 , 为线段延长线上一点,.给出下列结论:①;②;③.其中结论正确的序号有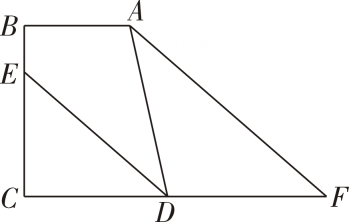
三、作图题(共2题,共14分)
-
16. 线段 , 交于点 , 为直线上一点(不与点 , 重合).过点在的右侧作射线 , 过点作直线 , 交于点(与不重合).(1)、如图1,若点在线段上,且为钝角.
①按要求补全图形;
②判断与的数量关系,并证明.
 (2)、若点在线段的延长线上,请直接写出与的数量关系
(2)、若点在线段的延长线上,请直接写出与的数量关系 17. [推理能力]如图,已知∠ABC=(2x+36)°.
17. [推理能力]如图,已知∠ABC=(2x+36)°.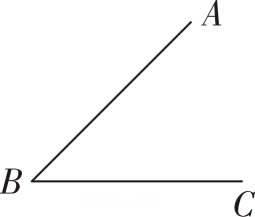 (1)、请你再画一个∠DEF,使得DE∥AB,EF∥BC,且DE交BC于点P.(2)、在(1)的条件下,∠ABC与∠DEF有怎样的数量关系?请说明理由.(3)、在(1)的条件下,若∠DEF=(3x+24)°,求x的值.
(1)、请你再画一个∠DEF,使得DE∥AB,EF∥BC,且DE交BC于点P.(2)、在(1)的条件下,∠ABC与∠DEF有怎样的数量关系?请说明理由.(3)、在(1)的条件下,若∠DEF=(3x+24)°,求x的值.四、解答题(共4题,共32分)
-
18. 如图,是河岸外一点.
 (1)、过点修一条与河岸平行的绿化带绿化带用直线表示 , 请画图表示;(2)、现用水管从河岸将水引到处,问:从河岸上的何处开口,才使所用的水管最短?画图表示,并说明设计的理由.19. 如图1, , 直线与、相交于点、 , 平分 , 平分 .
(1)、过点修一条与河岸平行的绿化带绿化带用直线表示 , 请画图表示;(2)、现用水管从河岸将水引到处,问:从河岸上的何处开口,才使所用的水管最短?画图表示,并说明设计的理由.19. 如图1, , 直线与、相交于点、 , 平分 , 平分 .

 (1)、求证:;(2)、如图2,为、之间一点(),若 , 求的度数;(3)、若为直线下方一点, , 为直线右侧一点,满足 , 则、、之间满足的数量关系是 .20. 如图,已知直线 , , 点E , F在上,且满足 , 平分 .
(1)、求证:;(2)、如图2,为、之间一点(),若 , 求的度数;(3)、若为直线下方一点, , 为直线右侧一点,满足 , 则、、之间满足的数量关系是 .20. 如图,已知直线 , , 点E , F在上,且满足 , 平分 . (1)、直线与有何位置关系?请说明理由;(2)、求的度数;(3)、若左右平移 , 在平移的过程中,
(1)、直线与有何位置关系?请说明理由;(2)、求的度数;(3)、若左右平移 , 在平移的过程中,①求与的比值;
②是否存在某种情况,使 , 若存在,求出的度数;若不存在,请说明理由.
21. 如图1,线段是由线段平移得到的.分别连接 , . 直线于点 , 延长与相交于点 . 点是射线上的一个动点,点不与点、点、点重合.连接 , .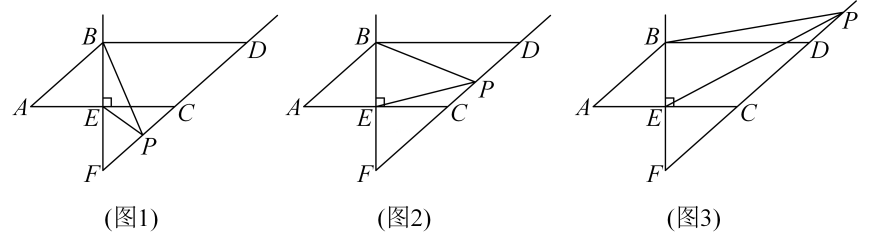 (1)、线段 , 的关系是;(2)、如图1,当点在线段上运动时, , , 之间的数量关系是;(3)、如图2,当点在线段上运动时, , , 之间的数量关系是否发生变化?若发生变化请写出它们的关系,并证明;若没有发生变化,请说明理由;(4)、如图3,当点在点上方运动时,请直接写出 , , 之间的数量关系: .
(1)、线段 , 的关系是;(2)、如图1,当点在线段上运动时, , , 之间的数量关系是;(3)、如图2,当点在线段上运动时, , , 之间的数量关系是否发生变化?若发生变化请写出它们的关系,并证明;若没有发生变化,请说明理由;(4)、如图3,当点在点上方运动时,请直接写出 , , 之间的数量关系: .五、实践探究题(共9题)
-
22. 综合与探究
数学活动课上,老师以“一个含的直角三角板和两条平行线”为背景展开探究活动,

如图1,已知直线 , 直角三角板中, , .
(1)、如图1,若 , 则;(直接写出答案)(2)、“启航”小组在图1的基础上继续展开探究:如图 , 调整三角板的位置,当三角板的直角顶点在直线上,直线与 , 相交时,他们得出的结论是: , 你认为启航小组的结论是否正确,请说明理由;(3)、如图 , 受到“启航”小组的启发,“睿智”小组提出的问题是:在图的基础上,继续调整三角板的位置,当点不在直线上,直线与 , 相交时,与有怎样的数量关系?请你用平行线的知识说明理由.