初中数学同步训练必刷提高卷（北师大版七年级下册 第二单元测试卷）
试卷更新日期：2024-03-09 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 如图，AB∥EF，FD平分∠EFC.若∠DFC=50°，则∠ABC的度数为（ ）
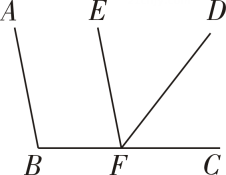A、50° B、60° C、100° D、120°2. 如图，已知AB∥CD，则图中与∠1相等的角有（ ）
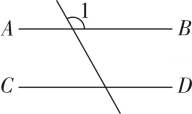A、5个 B、4个 C、3个 D、2个3. 如图所示的四个图形中，∠1和∠2是同位角的为（ ）
A、②③ B、①②③ C、①②④ D、①④4. 如图，下列条件中，能判定直线a∥b的是（ ）
A、∠1=∠2 B、∠1=∠5 C、∠3=∠5 D、∠1+∠4=1805. 在同一平面内，过直线l外一点P作l的垂线m，再过点P作m的垂线n ，则直线l与n的位置关系是（ ）A、相交 B、相交且垂直 C、平行 D、不能确定6. 如图，∠ACD是△ABC的外角，CE∥AB，若∠ACB=75°，∠ECD=50°，则∠A的度数为（ ）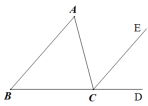
A、50° B、55° C、70° D、75°7. 如图，下列条件中，能判定a∥b的是（ ）
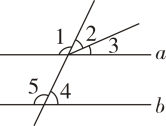A、∠1+∠4=180° B、∠2=∠4 C、∠1=∠4 D、∠5=∠2+∠38. 如图，与∠α构成同位角的角的个数为（ ）
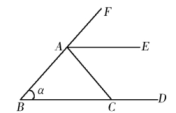A、1 B、2 C、3 D、49. 如图，给出下列条件：①∠B+∠BCD=180°；②∠1=∠2；③∠3=∠4；④∠B=∠5．其中能判定AB∥CD的条件有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，将三角形纸片ABC沿虚线剪掉两角得五边形CDEFG，若 ， ， 根据所标数据，则的度数为（ ）
A、54° B、64° C、66° D、72°二、填空题（每题3分，共15分）
-
11. 如图，已知∠1=∠2=∠3=59°，则∠4的度数为°.
12. 如图，点E，O，F 在同一条直线上，若AB∥EO，OF∥CD，则∠2+∠3-∠1=°.
13. 如图，∠A=70°，O是AB上一点，直线OD与AB 的夹角∠BOD=82°，要使 OD∥AC，直线 OD 应绕点O逆时针旋转至少 °.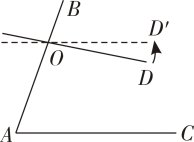
14. 如图1所示为一架消防云梯，它由救援台 AB、延展臂BC(点B在点C 的左侧)、伸展主臂CD、支撑臂EF 构成，在作业过程中，救援台 AB、车身GH 及地面MN 三者始终保持水平.现为参与一项高空救援工作，需要进行作业调整，如图2，使得延展臂 BC 与支撑臂 EF 所在直线互相垂直，且∠EFH=69°，则这时∠ABC=°.
15. 如图，含有角的直角三角板的两个顶点放在一个长方形的对边上，点为直角顶点， ， 延长交于点 ， 如果 ， 那么的度数是 ．
三、作图题（共2题，共15分）
-
16. 已知∠α如图，利用三角尺画出下列各角．
(1)、∠α的补角．(2)、∠α的余角．17. 根据下列要求画图：(1)、如图，
点A， B，C分别表示某公园平地上的三棵树，藏宝的地点D与这三棵树恰好构成一个平行四边形，请在图中作出所有可能的藏宝地点D的位置．
(2)、如图，已知点P和∠ABC，以点P为顶点画∠DPE，使得PD∥ BA，PE∥ BC，然用量角器量得：∠ABC=°，∠DPE=°，并猜想∠DPE与∠ABC的关系为 ．
四、解答题（共5题，共40分）
-
18. 如图， ， ．
(1)、试判断与的位置关系，并说明理由；(2)、若 ， ， 求的度数．19. 如图1，已知：AB∥CD，点E在CD上，且OE⊥OF．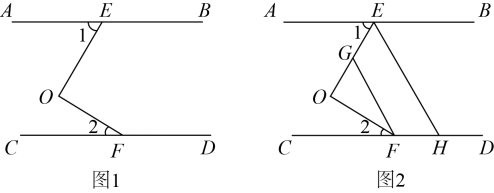
(1)、求证：∠1+∠2＝90°；(2)、如图2，分别在OE，CD上取点G，H，使FO平分∠CFG，EO平分∠AEH，求证：FG∥EH．20. 已知：如图，点D在线段上，过点D作交线段于点E，连接 ， 过点D作于点F，过点F作交线段于点G．
(1)、依题意补全图形；(2)、用等式表示与的数量关系，并证明．21. 已知，直线 AB∥CD，E为AB，CD间的一点，连结EA，EC．
(1)、如图①，若∠A= 20°，∠C=40°，则∠AEC=.(2)、如图②，若∠A=x°，∠C=y° ，则∠AEC= .(3)、如图③，若∠A=α，∠C=β，则α，β与∠AEC之间有何等量关系？请简要说明。22. 已知：点C是∠AOB的OA边上一点（点C不与点O重合），点D是∠AOB内部一点，射线CD不与OB相交．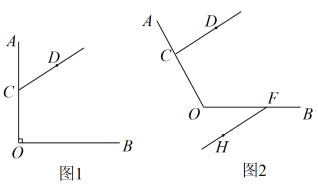
(1)、如图1，∠AOB＝90°，∠OCD＝120°，过点O作射线OE，使得OE//CD．（其中点E在∠AOB内部）．①依据题意，补全图1；
②直接写出∠BOE的度数．
(2)、如图2，点F是射线OB上一点，且点F不与点O重合，当时，过点F作射线FH，使得FH//CD（其中点H在∠AOB的外部），用含的代数式表示∠OCD与∠BFH的数量关系，并证明．