湖南省怀化市八县九校2023-2024学年八年级上学期数学期末考试试卷
试卷更新日期:2024-03-09 类型:期末考试
一、选择题(共10小题,每题3分,共30分)
-
1. 若 有意义,则的取值范围是( )A、 B、 C、或 D、2. 在下列图形中,正确画出AC边上的高的是( )A、
 B、
B、 C、
C、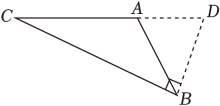 D、
D、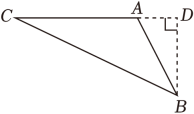 3. 下列结论:①无论a为何实数,都有意义;②当时, 分式的值为0;③若的值为负, 则x的取值范围是; ④若有意义,则x的取值范围是且.其中正确的个数是( )A、1 B、2 C、3 D、44. 若 , 则的值为( )A、1 B、0 C、 D、25. 若关于x的分式方程无解,则k的取值是( )A、 B、或 C、 D、或6. 若关于x的一元一次不等式的解为 , 则m的取值范围是( )A、 B、 C、 D、7. 如图,F是 的重心,连接AF并延长交BC于D,连接BF并延长交AC于 若 的面积是4,则四边形CDFE的面积是( )
3. 下列结论:①无论a为何实数,都有意义;②当时, 分式的值为0;③若的值为负, 则x的取值范围是; ④若有意义,则x的取值范围是且.其中正确的个数是( )A、1 B、2 C、3 D、44. 若 , 则的值为( )A、1 B、0 C、 D、25. 若关于x的分式方程无解,则k的取值是( )A、 B、或 C、 D、或6. 若关于x的一元一次不等式的解为 , 则m的取值范围是( )A、 B、 C、 D、7. 如图,F是 的重心,连接AF并延长交BC于D,连接BF并延长交AC于 若 的面积是4,则四边形CDFE的面积是( )
 A、2 B、5 C、3 D、48. 在△ABC和△A'B'C'中,∠B=∠B'=30°,AB=A'B'=6,AC=A'C'=4,已知∠C=n°,则∠C'=( )A、30° B、n° C、n°或180°-n° D、30°或150°9. 已知 , , 则( )A、35.12 B、351.2 C、111.08 D、1110.810. 如图,△ABC、△CDE 都是等腰三角形,且CA=CB , CD=CE , ∠ACB=∠DCE=α , AD , BE相交于点O , 点M , N分别是线段AD , BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC , 则OC平分∠AOE.正确的是( )
A、2 B、5 C、3 D、48. 在△ABC和△A'B'C'中,∠B=∠B'=30°,AB=A'B'=6,AC=A'C'=4,已知∠C=n°,则∠C'=( )A、30° B、n° C、n°或180°-n° D、30°或150°9. 已知 , , 则( )A、35.12 B、351.2 C、111.08 D、1110.810. 如图,△ABC、△CDE 都是等腰三角形,且CA=CB , CD=CE , ∠ACB=∠DCE=α , AD , BE相交于点O , 点M , N分别是线段AD , BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC , 则OC平分∠AOE.正确的是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题(共6小题,每题3分,共18分)
-
11. 已知一个正数的平方根是和 , 则这个数是 .12. 如果成立,那么满足它的所有整数的值是 .13. 下列命题中逆命题成立的有 . (填序号).
①同旁内角互补,两直线平行; ②如果两个角是直角,那么它们相等;
③如果 , 那么 , ; ④如果两个实数相等,那么它们的平方相等.
14. 当m=时,解关于x的分式方程会产生增根.15. 设表示不超过x的最大整数{例如:请你认真理解的意义,当 , 若 , 则的值为 .16. 观察下列等式:第1个等式:= ,
第个等式:= ,
第个等式: ,
第个等式:= ,
…
按上述规律,计算 .
三、解答题(共8小题,共72分)
-
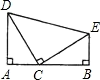
17. 计算:(1)、(2)、18. 解分式方程.(1)、(2)、19. 如图:在△CDE中,∠DCE=90°,CD=CE,DA⊥AB于A,EB⊥AB于B,试判断AB与AD,BE之间的关系,并证明.
 20. 若数a使关于x的不等式组有且只有四个整数解,且使关于y的方程的解为非负数,求符合条件的所有整数a之和.21. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
20. 若数a使关于x的不等式组有且只有四个整数解,且使关于y的方程的解为非负数,求符合条件的所有整数a之和.21. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)、求A、B两种型号的电风扇的销售单价;(2)、若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由。22. 我们知道,假分数可以化为整数与真分数的和的形式,例如: . 在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如: , , 这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如: , , 这样的分式就是假分式.类似地,假分式也可以化为整式与真分式的和的形式,如:; .(1)、分式是 分式(填“真”或“假”);(2)、将假分式、分别化为整式与真分式的和的形式;(3)、如果分式的值为整数,求出所有符合条件的整数x的值.23. 定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:(2+i)+(3﹣4i)=(2+3)+(i﹣4i)=5﹣3i
(1)、填空:i3= , i4= .(2)、填空:①(2+i)(2﹣i)=; ②(2+i)2= .(3)、若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知,(x+y)+3i=1﹣(x﹣y)i,(x,y为实数),求x,y的值.(4)、试一试:请利用以前学习的有关知识将 化简成a+bi的形式.(5)、解方程:x2﹣2x+4=0.24. 如图,A , B分别是两边 , 上的动点(均不与点O重合).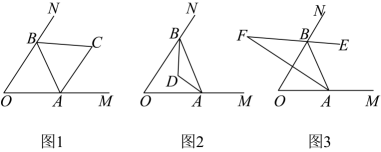 (1)、如图1,当时,的外角 , 的平分线交于点C , 则;(2)、如图2,当时, , 的平分线交于点D , 则(用含n的式子表示);(3)、如图3,当(α为定值,)时,是的平分线,的反向延长线与的平分线交于点F . 随着点A , B的运动,的大小会改变吗?如果不会,求出的度数(用含α的式子表示);如果会,请说明理由.
(1)、如图1,当时,的外角 , 的平分线交于点C , 则;(2)、如图2,当时, , 的平分线交于点D , 则(用含n的式子表示);(3)、如图3,当(α为定值,)时,是的平分线,的反向延长线与的平分线交于点F . 随着点A , B的运动,的大小会改变吗?如果不会,求出的度数(用含α的式子表示);如果会,请说明理由.