湖南省郴州市桂东县2023-2024学年七年级上学期数学期末考试试卷

试卷更新日期：2024-03-09 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共24分）

1. $- (- 2) ， - | - 7 | ， - | + 1 |$ ， $| - \frac{2}{3} |$ ， $- (+ \frac{11}{5})$ ，负数有（）个

A、1 B、2 C、3 D、4

查看试题解析
2. 据有关资料显示，2011年遵义市全年财政总收入202亿元，将202亿用科学记数法可表示（）

A、2.02×10² B、202×10⁸ C、2.02×10⁹ D、2.02×10¹⁰

查看试题解析
3. 若 $- 1 < a < 0$ ，则 $a ， \frac{1}{a} ， a^{2}$ 由小到大排列正确的是（）

A、 $a^{2} < a < \frac{1}{a}$ B、 $a < \frac{1}{a} < a^{2}$ C、 $\frac{1}{a} < a < a^{2}$ D、 $a < a^{2} < \frac{1}{a}$

查看试题解析
4. 在数轴上距2.5有3.5个单位长度的点所表示的数是（）

A、6 B、-6 C、-1 D、-1或6

查看试题解析
5. 下面计算正确的是（）

A、 $3 x^{2} - x^{2} = 3$ B、 $3 a^{2} + 2 a^{3} = 5 a^{5}$ C、 $3 + x = 3 x$ D、 $- 0.25 a b + \frac{1}{4} b a = 0$

查看试题解析
6. 下列变形错误的是（）

A、由 $4 - 3 x = 4 x - 3$ 得 $4 + 3 = 4 x + 3 x$ B、由 $- 3 (x - 2) = 2 (x + 1)$ 得 $- 3 x + 6 = 2 x + 2$ C、由 $- 2 x = 3$ 得 $x = - \frac{2}{3}$ D、 $由 \frac{x - 1}{3} + x = \frac{3 x + 1}{2}$ 分母得 $2 (x - 1) + 6 x = 3 (3 x + 1)$

查看试题解析
7. 如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（）

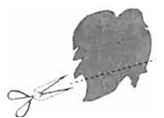A、垂线段最短 B、经过一点有无数条直线 C、两点之间，线段最短 D、经过两点，有且仅有一条直线

查看试题解析
8. 有理数 $a ， b$ 在数轴上对应的两点分别是 $A ， B$ ．计算 $A ， B$ ，两点之间的距离公式是（）

A、 $b - a$ B、 $| b | + | a |$ C、 $| b | - | a |$ D、 $| b - a |$

查看试题解析

二、填空题（每小题3分，共24分）

9. 一运动员某次跳水的最高点离跳板2m，记作+2m，则水面离跳板3m可以记作 m．

查看试题解析
10. 比x的15％大2的数是．

查看试题解析
11. 一个多项式减去3x等于 $5 x^{2} - 3 x - 5$ ，则这个多项式为．

查看试题解析
12. 已知实数a ，在数轴上如图所示，则|a﹣1|＝．

查看试题解析
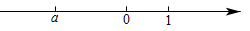13. 如果 $3 x^{5 a - 2} = - 6$ 是关于 $x$ 的一元一次方程，那么方程的解为．

查看试题解析
14. 当x=时，代数式 $\frac{3 - 2 x}{2}$ 与 $\frac{2 - x}{3}$ 互为相反数．

查看试题解析
15. 若 $∠ α$ 是它的余角的2倍， $∠ β$ 是 $∠ α$ 的2倍，那么 $∠ α + ∠ β =$ ．

查看试题解析
16. 一副三角板如图摆放，若 $∠ B A E = 135 °$ ，则 $∠ C A D$ 的度数是．

查看试题解析

三、解答题（第17-19题每题6分，第 20−23题每题8分，第24题10分，第25题12分，共72分）

17. 计算： $- 1^{4} + 0.5 \div {(- \frac{1}{2})}^{2} + {[3 + (- 1)]}^{4}$

查看试题解析
18. 解方程： $2 - \frac{2 x + 1}{3} = \frac{1 - x}{2}$

查看试题解析
19. 如图所示，外圆直径是 $D$ 厘米，内圆直径是 $d$ 厘米，四个小圆的直径都是2厘米，求图中阴影部分的面积（ $D > 4 + d$ ，结果保留π）．

查看试题解析
20. 化简求值： $- 6 (x^{2} y^{2} - x^{2}) + 3 (y^{2} + 2 x^{2} y^{2} - 2 x^{2})$ ，其中 $x = - 1 ， y = 2$ ．

查看试题解析
21. 某服装店以每件82元的价格购进了30套保暖内衣，销售时，针对不同的顾客，这30套保暖内衣的售价不完全相同.若以100元为标准.将超过的钱数记为正.不足的钱数记为负.则记录结果如表所示：

售出件数

7

6

7

8

2

售价（元）

+5

+1

0

-2

-5

请你求出该服装店在售完这30套保暖内衣后，共赚了多少钱?

查看试题解析
22. 某中学开展“每天阅读一小时”活动，根据学校实际情况，有以下四类读物供学生选择（每位学生必选一项）：A：科普类，B：文艺类，C：文学类，D：其他类．为了了解学生最喜欢哪一类读物，随机抽取了部分学生调查，将调查结果绘制了如下不完整的统计图．请根据统计图回答下列问题：

(1)、本次调查的样本容量为．

(2)、补全条形统计图．

(3)、扇形统计图中，“文艺类”所对应的扇形圆心角的度数为度．

(4)、该学校计划订购20000册上述四类课外读物，根据学生爱好，为满足学生需求，学校大约订购本“文学类”课外读物．

查看试题解析
23. 某单位元旦期间组织员工出游，原计划租用28座客车若干辆，但有4人没有座位，若租用同样数量的33座客车，只有一辆空余了11个座位，其余客车都已坐满，求该单位组织出游的员工人数．

查看试题解析
24.

(1)、根据给出字母的值代入计算，结果填入下表：
$a$
$b$
$a^{2} - 2 a b + b^{2}$
${(a - b)}^{2}$
3
2
    ▲
    ▲
$- 5$
1
    ▲
    ▲
4
$- 2$
    ▲
    ▲

(2)、再取一些 $a$ 和 $b$ 的值代入计算，对比结果猜测： $a^{2} - 2 a b + b^{2}$ ${(a - b)}^{2}$ ．

(3)、利用你的猜测计算： $3.2 3^{2} - 2 \times 3.23 \times 0.23 + 0.2 3^{2}$ ．

查看试题解析
25. 数轴上有A、B、C个点，分别表示有理数 $- 10 ， - 5 ， 5$ ，动点P从A出发，以每秒1个单位的速度向终点C移动，移动时间为t秒．

(1)、用含t的代数式表示P对应的数字为．

(2)、当P运动到B时，Q从A出发以每秒3个单位的速度向C运动，Q到达C后，立即以同样的速度返回，运动到终点A时停止．在Q开始运动后：
①请用含t的代数式表示：Q的移动时间为 ▲ ， Q未到达C前Q到C的距离 $Q C =$ ▲ ， Q到达C后Q到C的距离 $Q C =$ ▲ ．
②P、Q两点之间的距离能否为3个单位？如果能，请求出此时t的值；如果不能，请说明理由．

查看试题解析

$a$	$b$	$a^{2} - 2 a b + b^{2}$	${(a - b)}^{2}$
3	2	▲	▲
$- 5$	1	▲	▲
4	$- 2$	▲	▲

售出件数	7	6	7	8	2
售价（元）	+5	+1	0	-2	-5