湖南省怀化市八县九校联合调研考试2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-03-09 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 已知一元二次方程x2+kx-3=0有一个根为1,则k的值为( )A、−2 B、2 C、−4 D、42. 如图为甲、乙、丙、丁四名射击运动员在赛前的某次射击选拔赛中,各射击10次成绩的折线图和表示平均数的水平线,经过计算,四人成绩的方差关系为:s甲2=s乙2 , s丙2=s丁2 , 要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
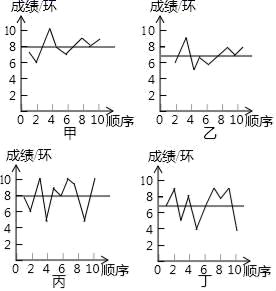 A、甲 B、乙 C、丙 D、丁3. 二次函数为常数的图象如图所示,则方程有一正实数根和一负实数根的条件是( )
A、甲 B、乙 C、丙 D、丁3. 二次函数为常数的图象如图所示,则方程有一正实数根和一负实数根的条件是( ) A、 B、 C、 D、4. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( )
A、 B、 C、 D、4. 由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( ) A、 B、 C、 D、5. 方程的两个根为( )A、 B、 C、 D、6. 在同一平面直角坐标系中,函数与 (k为常数且)的图象大致是( )A、
A、 B、 C、 D、5. 方程的两个根为( )A、 B、 C、 D、6. 在同一平面直角坐标系中,函数与 (k为常数且)的图象大致是( )A、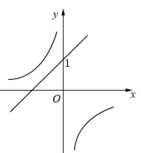 B、
B、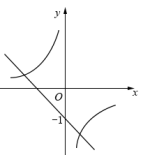 C、
C、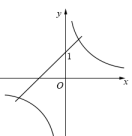 D、
D、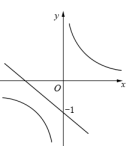 7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、8. 抛物线(a , b , c为常数)的对称轴为 , 过点和点 , 且 . 有下列结论:①;②对任意实数m都有:;③;④若 , 则 . 其中正确结论的个数为( )A、1个 B、2个 C、3个 D、4个9. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )
A、 B、 C、 D、8. 抛物线(a , b , c为常数)的对称轴为 , 过点和点 , 且 . 有下列结论:①;②对任意实数m都有:;③;④若 , 则 . 其中正确结论的个数为( )A、1个 B、2个 C、3个 D、4个9. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )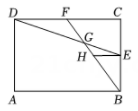 A、 B、1 C、 D、10. 如图,等边三角形ABC中,AB=3,点D在边AB上,且AD=1,点E是边B上的一动点,作射线ED.射线ED绕点E顺时针旋转60°得到射线EF,交AC于点F,则点E从B→C的运动过程中,CF的最大值是( )
A、 B、1 C、 D、10. 如图,等边三角形ABC中,AB=3,点D在边AB上,且AD=1,点E是边B上的一动点,作射线ED.射线ED绕点E顺时针旋转60°得到射线EF,交AC于点F,则点E从B→C的运动过程中,CF的最大值是( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题(每题3分,共18分)
-
11. 已知关于x的一元二次方程没有实数根,那么a的取值范围是 .12. 如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离 为海里.
 13. 一元二次方程 配方为 ,则k的值是.14. 如图,直线与反比例函数交于点B , 与x轴和y轴分别交于点A和点D , 于点C , 若点D是线段的中点, , , 则k的值为 .
13. 一元二次方程 配方为 ,则k的值是.14. 如图,直线与反比例函数交于点B , 与x轴和y轴分别交于点A和点D , 于点C , 若点D是线段的中点, , , 则k的值为 . 15. 如图,A , B是双曲线y=(x>0)上的两点,连接OA , OB.过点A作AC⊥x轴于点C , 交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m , 2),则m的值为 .
15. 如图,A , B是双曲线y=(x>0)上的两点,连接OA , OB.过点A作AC⊥x轴于点C , 交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m , 2),则m的值为 . 16. 阅读材料:在中, , , 求的值.
16. 阅读材料:在中, , , 求的值.解题思路:在上截取 , 再连接 , 可证为等腰三角形,设 , 则 , 则 , .

三、解答题(共72分)
-
17. 解方程:(1)、;(2)、 .18. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 , 连接.
 (1)、求的值;(2)、观察函数图象,直接写出不等式的解集;(3)、求的面积.19. 如图,在中, , D为上一点,且 .
(1)、求的值;(2)、观察函数图象,直接写出不等式的解集;(3)、求的面积.19. 如图,在中, , D为上一点,且 . (1)、求证:;(2)、当 , 且的面积为10时,求的面积.20. 某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 , 这时地面上的点E , 标杆的顶端点D , 古塔的塔尖点B正好在同一直线上,测得米,将标杆向后平移到点G处,这时地面上的点F , 标B杆的顶端点H , 古塔的塔尖点B正好在同一直线上(点F , 点G , 点E , 点C与古塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算古塔的高度AB .
(1)、求证:;(2)、当 , 且的面积为10时,求的面积.20. 某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆 , 这时地面上的点E , 标杆的顶端点D , 古塔的塔尖点B正好在同一直线上,测得米,将标杆向后平移到点G处,这时地面上的点F , 标B杆的顶端点H , 古塔的塔尖点B正好在同一直线上(点F , 点G , 点E , 点C与古塔底处的点A在同一直线上),这时测得米,米,请你根据以上数据,计算古塔的高度AB . 21. 在中, , , , 点从点出发沿边向点以的速度移动,点从点出发沿边向点以的速度移动.
21. 在中, , , , 点从点出发沿边向点以的速度移动,点从点出发沿边向点以的速度移动. (1)、如果 , 同时出发,几秒钟后,可使的面积为平方厘米?(2)、点 , 在移动过程中,是否存在某一时刻,使得的面积等于的面积的一半?若存在,求出运动的时间;若不存在,说明理由.(3)、点 , 在移动过程中,是否存在某一时刻,使得的面积最大?若存在,求出运动的时间和最大的面积;若不存在,说明理由.22. 某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系,可以近似的看作一次函数 . (利润售价制造成本)(1)、写出每月的利润z(万元)与销售单价x(元)之间的函数表达式;(不必写出x的取值范围)(2)、当销售单价定为多少元时,厂商每月能获得350万元的利润?当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?23. 定义:已知 , 是关于x的一元二次方程的两个实数根,若 , 且 , 则称这个方程为“限根方程”.如:一元二次方程的两根为 , , 因为 , , 所以一元二次方程为“限根方程”.
(1)、如果 , 同时出发,几秒钟后,可使的面积为平方厘米?(2)、点 , 在移动过程中,是否存在某一时刻,使得的面积等于的面积的一半?若存在,求出运动的时间;若不存在,说明理由.(3)、点 , 在移动过程中,是否存在某一时刻,使得的面积最大?若存在,求出运动的时间和最大的面积;若不存在,说明理由.22. 某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系,可以近似的看作一次函数 . (利润售价制造成本)(1)、写出每月的利润z(万元)与销售单价x(元)之间的函数表达式;(不必写出x的取值范围)(2)、当销售单价定为多少元时,厂商每月能获得350万元的利润?当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?23. 定义:已知 , 是关于x的一元二次方程的两个实数根,若 , 且 , 则称这个方程为“限根方程”.如:一元二次方程的两根为 , , 因为 , , 所以一元二次方程为“限根方程”.请阅读以上材料,回答下列问题:
(1)、判断一元二次方程是否为“限根方程”,并说明理由;(2)、若关于x的一元二次方程是“限根方程”,且方程的两根、满足 , 求k的值.24. 如图,抛物线与x轴交于A、B两点,与y轴交于点C , 抛物线的对称轴交x轴于点D , 已知 , . (1)、求抛物线的表达式;(2)、点E是线段上的一个动点,过点E作x轴的垂线与抛物线相交于点F , 当点E运动到什么位置时,的面积最大?求出的最大面积及此时E点的坐标;(3)、在坐标平面内是否存在点P , 使得以A , C , D , P为顶点的四边形是平行四边形?如果存在,直接写出P点的坐标;如果不存在,请说明理由.
(1)、求抛物线的表达式;(2)、点E是线段上的一个动点,过点E作x轴的垂线与抛物线相交于点F , 当点E运动到什么位置时,的面积最大?求出的最大面积及此时E点的坐标;(3)、在坐标平面内是否存在点P , 使得以A , C , D , P为顶点的四边形是平行四边形?如果存在,直接写出P点的坐标;如果不存在,请说明理由.