吉林省松原市乾安县2023-2024学年八年级上学期数学期末试卷

试卷更新日期：2024-03-09 类型：期末考试

进入出卷网下载

一、选择题：本题共6小题，每小题2分，共12分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 长度分别为 $2$ ， $7$ ， $x$ 的三条线段能组成一个三角形， $x$ 的值可以是（）

A、 $4$ B、 $5$ C、 $6$ D、 $9$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} \cdot a^{6} = a^{8}$ B、 $a^{8} \div a^{4} = a^{2}$ C、 $2 a^{2} + 3 a^{2} = 6 a^{4}$ D、 $(- 3 a)^{2} = - 9 a^{2}$

查看试题解析
3. 若 $x = - 1$ ，则下列分式值为 $0$ 的是（）

A、 $\frac{x^{2}}{x}$ B、 $\frac{x}{x + 1}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x^{2} - 1}{x}$

查看试题解析
4. 下面四幅画分别是体育运动长鼓舞，武术，举重、摔跤抽象出来的简笔画，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（）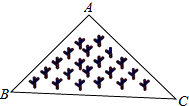

A、△ABC的三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三边的中垂线的交点

查看试题解析
6. 已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动，设点P的运动时间为 $t$ 秒，当 $t$ 的值为（）秒时，△ABP和△DCE全等．

A、1 B、1或3 C、1或7 D、3或7

查看试题解析

二、填空题：本题共8小题，每小题3分，共24分。

7. 分解因式：3x²y-3y＝.

查看试题解析
8. 化简： $\frac{5 b + 1}{b^{2}} - \frac{2 b + 1}{b^{2}} =$ ．

查看试题解析
9. 某微生物的直径为0.000 005 035m ，用科学记数法表示该数为．

查看试题解析
10. 若等腰三角形的一个外角为 $140 °$ ，则它的顶角的度数为．

查看试题解析
11. 如图， $∠ A C B = 90 °$ ， $A D ⊥ C E$ ， $B E ⊥ C E$ ，垂足分别为 $D$ ， $E$ ，添加一个条件，使 $△ A C D$ ≌ $△ C B E$ ，添加的条件是 $. ($ 写出一个即可 $)$

查看试题解析
12. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ， $D E ⊥ A B .$ 若 $A C = 2$ ， $D E = 1$ ，则 $S_{△ A C D} =$ ．

查看试题解析
13. 如图，在三角形纸片 $A B C$ 中， $A C = B C .$ 把 $△ A B C$ 沿着 $A C$ 翻折，点 $B$ 落在点 $D$ 处，连接 $B D .$ 如果 $∠ B A C = 35 °$ ，则 $∠ C B D$ 的度数是．

查看试题解析
14. 如图，在平面直角坐标系中，点 $A$ 在 $x$ 轴上，点 $B$ 在 $y$ 轴上，点 $C$ 在 $A B$ 的延长线上 $.$ 过点 $C$ 作 $C D ⊥ A C$ ，与 $y$ 轴交于点 $D$ ，且 $C D = O A .$ 若点 $D$ 的坐标为 $(0，6)$ ，则线段 $A C$ 的长度为．

查看试题解析

三、计算题：本大题共1小题，共5分。

15. 解分式方程： $\frac{2 - x}{x - 3}$ + $\frac{1}{3 - x}$ =1．

查看试题解析

四、解答题：本题共11小题，共79分。解答应写出文字说明，证明过程或演算步骤。

16. 计算：

(1)、 $(12 x^{4} - 8 x^{3}) \div 2 x$ ；

(2)、 $\frac{1}{3} a (3 a - 6) + (a - 2) (a + 3)$ ．

查看试题解析
17.
如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 为 $A C$ 上一点，且满足 $A D = B D = B C .$ 点 $F$ 在 $B C$ 延长线上，连接 $F D$ 并延长，交 $A B$ 于点 $E$ ，连接 $A F$ ，求 $∠ B A C$ 和 $∠ A C B$ 的度数．

查看试题解析
18. 如图， $B E = C F$ ， $A C = D F$ ， $A C / / D F .$ 求证： $△ A B C$ ≌ $△ D E F$ ．

查看试题解析
19. 某中学要举行校庆活动，现计划在教学楼之间的广场上搭建舞台 $.$ 已知广场中心有一座边长为 $b$ 的正方形的花坛，学生会提出两个方案：
方案一：如图 $1$ ，绕花坛搭建外围是正方形的“回”字形舞台 $($ 阴影部分 $)$ ，面积为 $S_{1}$ ；
方案二：如图 $2$ ，在花坛的三面搭建“凹”字形舞台 $($ 阴影部分 $)$ ，面积为 $S_{2}$ ；具体数据如图所示．

(1)、图 $2$ 长方形的长是 ▲ ，宽是 ▲ ；

(2)、试比较 $S_{1}$ 与 $S_{2}$ 的大小关系．

查看试题解析
20. 图①、图②、图③都是3×3的正方形网格，每个小正方形的顶点称为格点．A，B，C均为格点．在给定的网格中，按下列要求画图：

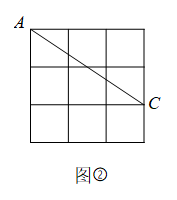
(1)、在图①中，画一条不与AB重合的线段MN，使MN与AB关于某条直线对称，且M，N为格点．

(2)、在图②中，画一条不与AC重合的线段PQ，使PQ与AC关于某条直线对称，且P，Q为格点．

(3)、在图③中，画一个△DEF，使△DEF与△ABC关于某条直线对称，且D，E，F为格点．

查看试题解析
21. 下面是一位同学化简代数式 $(\frac{2 x}{x + 2} - x) \div \frac{x^{2} - 2 x}{x + 2}$ 的解答过程：
解：原式 $= \frac{2 x - x^{2} + 2 x}{x + 2} \cdot \frac{x + 2}{x (x - 2)} ①$
$= \frac{x (4 - x)}{x + 2} \cdot \frac{x + 2}{x (x - 2)} ②$ $= \frac{4 - x}{x - 2} ③$

(1)、这位同学的解答，在第 ▲ 步出现错误．

(2)、请你写出正确的解答过程，并求出当 $x = 4$ 时，原式的值．

查看试题解析
22. 2022年我国已成为全球最大的电动汽车市场，电动汽车在保障能源安全，改善空气质量等方面较传统汽车都有明显优势，经过对某款电动汽车和某款燃油车的对比调查发现，电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元．若充电费和加油费均为200元时，电动汽车可行驶的总路程是燃油车的4倍，求这款电动汽车平均每公里的充电费．

查看试题解析
23. 如图，一个小长方形的长为 $a + b$ ，宽为 $a$ ，把 $6$ 个大小相同的小长方形放入到大长方形内．

(1)、大长方形的宽 $m =$ ▲ ，长 $n =$ ▲ $($ 长和宽都用含 $a$ ， $b$ 的式子来表示 $)$ ．

(2)、求在大长方形中，阴影部分的面积 $($ 用含 $a$ ， $b$ 的式子来表示 $)$

(3)、若 $b = 2 a$ ，大长方形面积为 $S_{1}$ ，大长方形内阴影部分的面积为 $S_{2}$ ，则 $\frac{S_{2}}{S_{1}} =$ ▲ ．

查看试题解析
24.

(1)、【感知】如图 $①$ ， $△ A B C$ 是等边三角形， $D$ 是边 $B C$ 上一点 $($ 点 $D$ 不与点 $B$ 、 $C$ 重合 $)$ ，作 $∠ E D F = 60 °$ ，使角的两边分别交边 $A B$ 、 $A C$ 于点 $E$ 、 $F$ ，且 $B D = C F .$ 若 $D E ⊥ B C$ ，则 $∠ D F C$ 的大小是 ▲ 度；

(2)、【探究】如图 $②$ ， $△ A B C$ 是等边三角形， $D$ 是边 $B C$ 上一点 $($ 点 $D$ 不与点 $B$ 、 $C$ 重合 $)$ ，作 $∠ E D F = 60 °$ ，使角的两边分别交边 $A B$ 、 $A C$ 于点 $E$ 、 $F$ ，且 $B D = C F .$ 求证： $B E = C D$ ；

(3)、在图 $③$ 中，若 $D$ 是边 $B C$ 的中点，且 $A B = 2$ ，其它条件不变，如图 $③$ 所示，则四边形 $A E D F$ 的周长为 ▲ ．

查看试题解析
25. 由角平分线不仅可以得到角相等，也可以用来构造全等三角形，其构造思路如下：

在图 $1$ 中，点 $P$ 是 $∠ A B C$ 的平分线 $O C$ 上一点，点 $M$ 在 $O A$ 上，我们可以在 $O B$ 上截取 $O N =$ ▲ ；连接 $P N$ ，根据三角形全等判定方法 ▲ ；构造出全等三角形 $△ O M P$ ≌ $△ O N P$ ．

(1)、请补全上面的构造思路；

(2)、参考上面的思路，解答问题：
如图 $2$ ，在 $△ A B C$ 中， $A C > B C$ ，直线 $M N$ 垂直平分 $B C$ ，与 $∠ B A C$ 的平分线 $A E$ 交于 $D$ 点，连接 $C D$ 、 $B D$ ，则 $∠ A B D$ 与 $∠ A C D$ 有何数量关系，说明理由．

查看试题解析
26. 如图 $(1)$ ，在 $△ A B C$ 中，已知 $A B = B C = C A = 4 c m$ ， $A D ⊥ B C$ 于 $D$ ，点 $P$ 、 $Q$ 分别从 $B$ 、 $C$ 两点同时出发，其中点 $P$ 沿 $B C$ 向终点 $C$ 运动，速度为 $1 c m / s$ ：点 $Q$ 沿 $C A$ 、 $A B$ 向终点 $B$ 运动，速度为 $2 c m / s$ ，设它们运动的时间为 $x (s)$ ．

(1)、当 $x =$ ▲ 时， $P Q ⊥ A C$ ；

(2)、当 $0 < x < 2$ 时，求出使 $P Q / / A B$ 的 $x$ 值；

(3)、当 $2 < x < 4$ 时，是否存在 $x$ ，使 $△ B P Q$ 是直角三角形？若存在，请求出 $x$ 的值，若不存在请说明理由．

查看试题解析