吉林省长春市九台区2023-2024学年九年级上学期数学期末测试卷
试卷更新日期:2024-03-09 类型:期末考试
一、单项选择题(每小题2分,共12分)
-
1. 方程3+9=0的根为( )A、3 B、-3 C、±3 D、无实数根2. 如图,是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数这个几何体的主视图是( )
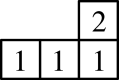 A、
A、 B、
B、 C、
C、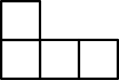 D、
D、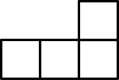 3. 在和中, , 添加下列条件不能判定两个三角形相似的是( )A、 B、 C、 D、4. 在中, , , 则的值为( )A、 B、 C、 D、5. 将抛物线向右平移1个单位得到的抛物线是( )A、 B、 C、 D、6. 如果点、在反比例函数的图象上,若 , 则与的大小关系是( )A、 B、 C、 D、不能确定
3. 在和中, , 添加下列条件不能判定两个三角形相似的是( )A、 B、 C、 D、4. 在中, , , 则的值为( )A、 B、 C、 D、5. 将抛物线向右平移1个单位得到的抛物线是( )A、 B、 C、 D、6. 如果点、在反比例函数的图象上,若 , 则与的大小关系是( )A、 B、 C、 D、不能确定二、填空题(每小题3分,共24分)
-
7. 点关于原点对称的点的坐标是 .8. 底角相等的两个等腰三角形相似.(填“一定”或“不一定”)9. 如果为实数,且满足 , 那么 .10. 二次函数 的顶点坐标 .11. 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了米.
 12. 如图,将等边放在平面直角坐标系中,点A的坐标为 , 点B在第一象限,将等边绕点O顺时针旋转180°得到 , 则点的坐标是 .
12. 如图,将等边放在平面直角坐标系中,点A的坐标为 , 点B在第一象限,将等边绕点O顺时针旋转180°得到 , 则点的坐标是 . 13. 在⊙O 中,AB 是直径,弦 CD 与 AB 相交于点 E,若 , 则 CE=DE(只需填一个适合的条件).14. 如图,矩形的对角线经过坐标原点 , 矩形的边分别平行于坐标轴,点在反比例函数的图象上.若点的坐标为 , 则的值为 .
13. 在⊙O 中,AB 是直径,弦 CD 与 AB 相交于点 E,若 , 则 CE=DE(只需填一个适合的条件).14. 如图,矩形的对角线经过坐标原点 , 矩形的边分别平行于坐标轴,点在反比例函数的图象上.若点的坐标为 , 则的值为 .
三、解答题(每小题5分,共20分)
-
15. 若代数式的值与的值互为相反数,求的值.16. 已知二次函数y=2x2+bx+1的图象过点(2,3).(1)、求该二次函数的表达式;(2)、若点P(m , m2+1)也在该二次函数的图象上,求点P的坐标.17. 如图,四边形、、都是正方形.
 (1)、求证:;(2)、求的度数.18. 在反比例函数的图象上有不重合的两点、 , 点的纵坐标为2.(1)、求点的横坐标;(2)、过点向轴作垂线,垂足是 , 试求 .
(1)、求证:;(2)、求的度数.18. 在反比例函数的图象上有不重合的两点、 , 点的纵坐标为2.(1)、求点的横坐标;(2)、过点向轴作垂线,垂足是 , 试求 .四、解答题(每小题7分,共28分)
-
19. 某种流感病毒,若有一人患了这种流感,则在每轮传染中一人将平均传染x人.(1)、现有一人患上这种流感,求第一轮传染后患病的人数(用含x的代数式表示);(2)、在进入第二轮传染前,有两位患者被及时隔高并治愈,问第二轮传染后患病的人数会有21人吗?20. 四张大小、质地均相同的卡片上分别标有数字1,2,3,4,现将标有数字的一面朝下扣在桌子上,从中随机抽取一张(不放回),再从桌子上剩下的3张中随机抽取第二张.(1)、用画树状图的方法,列出前后两次抽得的卡片上所标数字的所有可能情况;(2)、计算抽得的两张卡片上的数字之积为奇数的概率是多少?21. 如图,在平面直角坐标系xOy中,每个小正方形的边长都为1,和的顶点都在格点上,回答下列问题:
 (1)、可以看作是经过若干次图形的变化平移、轴对称、旋转得到的,写出一种由得到的过程:;(2)、画出绕点B逆时针旋转的图形;(3)、在中,点C所形成的路径的长度为 .22. 如图,一辆摩拜单车放在水平的地面上,车把头下方处与坐垫下方处在平行于地面的水平线上,、之间的距离约为 , 现测得、与的夹角分别为与 . 若点到地面的距离为 , 坐垫中轴处与点间的距离为 , 求点到地面的距离.(结果保留一位小数参考数据: , , )
(1)、可以看作是经过若干次图形的变化平移、轴对称、旋转得到的,写出一种由得到的过程:;(2)、画出绕点B逆时针旋转的图形;(3)、在中,点C所形成的路径的长度为 .22. 如图,一辆摩拜单车放在水平的地面上,车把头下方处与坐垫下方处在平行于地面的水平线上,、之间的距离约为 , 现测得、与的夹角分别为与 . 若点到地面的距离为 , 坐垫中轴处与点间的距离为 , 求点到地面的距离.(结果保留一位小数参考数据: , , )
五、解答题(每小题8分,共16分)
-
23. 如图:一次函数的图象与反比例函数的图象交于、两点.
 (1)、求反比例函数和一次函数的解析式;(2)、求的面积.24. 如图,BE是圆O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C,
(1)、求反比例函数和一次函数的解析式;(2)、求的面积.24. 如图,BE是圆O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C,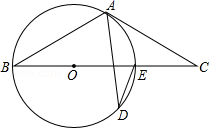 (1)、若∠ADE=25°,求∠C的度数;(2)、若AB=AC,CE=2,求⊙O半径的长.
(1)、若∠ADE=25°,求∠C的度数;(2)、若AB=AC,CE=2,求⊙O半径的长.六、解答题(每小题10分,共20分)
-
25. 已知:二次函数 .(1)、求证:该抛物线与轴一定有两个交点;(2)、设抛物线与轴的两个交点是、(在原点左边,在原点右边),且 , 求此时抛物线的解析式;(3)、在(2)的前提下,若抛物线与轴交于点 , 问在轴的正半轴上是否存在点 , 使和相似?26. 如图,在矩形中, , 为边上一点, , 连接 . 动点从点同时出发,点以的速度沿向终点运动;点以的速度沿折线向终点运动.设点运动的时间为 , 在运动过程中,点 , 点经过的路线与线段围成的图形面积为 .

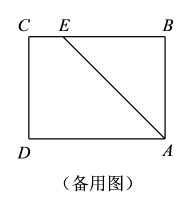 (1)、 , ;(2)、求关于的函数解析式,并写出自变量的取值范围;(3)、当时,直接写出的值.
(1)、 , ;(2)、求关于的函数解析式,并写出自变量的取值范围;(3)、当时,直接写出的值.