浙江省杭州市2023-2024学年高一上学期期末学业水平测试数学试题

试卷更新日期：2024-03-08 类型：期末考试

进入出卷网下载

一、单选题：

1. 设集合 $A = {x | x (x - 3) < 0} ， B = {1 ， 2 ， 3}$ ，则 $A ∩ B =$ （）

A、 ${2}$ B、 ${3}$ C、 ${1 ， 2}$ D、 ${0 ， 1 ， 2 ， 3}$

查看试题解析
2. 若 $a ， b \in R$ ，则 “ $a b > 2$ ” 是“ $a > \sqrt{2}$ 且 $b > \sqrt{2}$ ” 的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 函数 $f (x) = l n x + \frac{1}{x - 1}$ 的定义域为（）

A、 $(0 ， + \infty)$ B、 $(1 ， + \infty)$ C、 $(0 ， 1) ∪ (1 ， + \infty)$ D、 $(- \infty ， 1) ∪ (1 ， + \infty)$

查看试题解析
4. 为了得到函数 $y = 2 s i n 2 x$ 的图象，只需把函数 $y = 2 s i n (2 x + 1)$ 图象上的所有的点（）

A、向左平移1个长度单位 B、向右平移1个长度单位 C、向左平移 $\frac{1}{2}$ 个长度单位 D、向右平移 $\frac{1}{2}$ 个长度单位

查看试题解析
5. 若函数 $f (x) = {\begin{array}{l} 2^{x} - 3 ， x > 0 \\ g (x) ， x < 0 \end{array}$ 是奇函数，则 $g (- 2) =$ （）

A、1 B、 $- 1$ C、 $- \frac{11}{4}$ D、 $\frac{11}{4}$

查看试题解析
6. 若 $s i n θ + c o s θ = \frac{\sqrt{10}}{5} (0 < θ < π)$ ，则 $t a n θ + 2 s i n θ c o s θ$ 的值为（）

A、 $- \frac{33}{10}$ B、 $- \frac{18}{5}$ C、 $- \frac{9}{5}$ D、 $\frac{12}{5}$

查看试题解析
7. 已知 $a > 1 ， b > 0$ ，且 $a + \frac{1}{b} = 2$ ，则 $\frac{4}{a - 1} + b$ 的最小值为（）

A、4 B、6 C、8 D、9

查看试题解析
8. 已知函数 $f (x) = \sqrt{x + 2} + \frac{1}{a x + 1} > 0 (a \in R)$ ，若对于定义域内任意一个自变量 $x$ 都有 $f (x) > 0$ ，则 $a$ 的最大值为（）

A、0 B、 $\frac{1}{2}$ C、1 D、2

查看试题解析

二、多选题: 本题共 4 小题, 每小题 5 分, 共 20 分.在每小题给出的四个选项中, 有多项符合题目要求, 全部选对的得 5 分, 部分选对的得 2 分, 有选错的或不选的得 0 分.

9. 下列各式的值为 $\frac{1}{2}$ 的是（）

A、 $s i n (- 93 0^{∘})$ B、 $2 s i n \frac{π}{12} s i n \frac{5 π}{12}$ C、 $c o s 3 3^{∘} c o s 2 7^{∘} + s i n 3 3^{∘} s i n 2 7^{∘}$ D、 $\frac{t a n 22 . 5^{∘}}{1 - t a n^{2} 22 . 5^{∘}}$

查看试题解析
10. 下列函数的值域为 $R$ 且在定义域上单调递增的函数是（）

A、 $f (x) = {(x - 1)}^{3}$ B、 $f (x) = 202 3^{x}$ C、 $f (x) = l o g_{2023} x$ D、 $f (x) = {\begin{array}{l} - \frac{1}{x} & ， x \neq 0 \\ 0 & ， x = 0 \end{array}$

查看试题解析
11. 高斯是德国著名的数学家，近代数学奠基者之一，享有 “数学王子” 的美誉，用其名字命名的 “高斯函数”：设 $x \in R$ ，用 $[x]$ 表示不超过 $x$ 的最大整数，则 $y = [x]$ 称为高斯函数，也叫取整函数，则下列叙述正确的是（）

A、 $[c o s \frac{π}{4}] = 0$ B、函数 $y = c o s x - [c o s x]$ 有3个零点 C、 $y = [c o s x]$ 的最小正周期为 $2 π$ D、 $y = [c o s x]$ 的值域为 ${- 1 ， 0 ， 1}$

查看试题解析
12. 已知函数 $f (x) = s i n (ω x + φ) (ω > 0)$ 在区间 $(\frac{π}{6} ， \frac{2 π}{3})$ 上单调遂增，则下列判断中正确的是（）

A、 $ω$ 的最大值为 2 B、若 $φ = - \frac{π}{6}$ ，则 $ω \in (0 ， 1]$
C、若 $f (\frac{5 π}{12}) > 0$ ，则 $f (\frac{π}{6}) + f (\frac{2 π}{3}) < 0$ D、若函数 $y = f (x) - \frac{\sqrt{3}}{2}$ 两个零点间的最小距离为 $\frac{π}{6}$ ，则 $ω = 2$

查看试题解析

三、填空题: 本题共4小题, 每小题5分, 共20分.把答案填在答题卡中的横线上.

13. $l o g_{\frac{1}{3}} 5 - l o g_{\frac{1}{3}} 45 + 4^{\frac{3}{2}}$ 的值为.

查看试题解析
14. 已知函数 $f (x)$ 的定义域为 $R$ ，且满足 $f (x) + f (- x) = 0 ， f (x + 1) - f (- x) = 0$ ，则 $f (x)$ 可以是.(写出一个即可)

查看试题解析
15. 已知 $s i n (α + \frac{π}{4}) = \frac{3}{5} ， 0 < α < π$ ，则 $c o s (2 α + \frac{π}{4})$ 的值为.

查看试题解析
16. 已知下列五个函数： $y = x ， y = \frac{1}{x} ， y = x^{2} ， y = l n x ， y = e^{x}$ ，从中选出两个函数分别记为 $f (x)$ 和 $g (x)$ ，若 $F (x) = f (x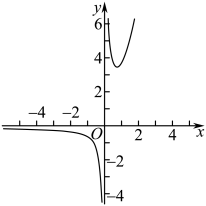) + g (x)$ 的图象如图所示，则 $F (x) =$ ．

查看试题解析

四、解答题：本题共 6 小题, 共 70 分.解答应写出文字说明, 证明过程或演算步骤

17. 已知集合 $A = {x | y = \sqrt{- 2 x^{2} + x + 1}}$ ，集合 $B = {x | (x + a - 1) (x - 2 a) \geq 0 ， a \in R}$ .

(1)、当 $a = 1$ 时，求 $∁_{R} (A ∪ B)$ ；

(2)、若 $A ∩ B = A$ ，求实数 $a$ 的值.

查看试题解析
18. 如图所示，在平面直角坐标系 $x O y$ 中，角 $α$ 和角 $β (0 < α < \frac{π}{2} < β < \frac{2 π}{3})$ 的顶点与坐标原点重合，始边与 $x$ 轴的非负半轴重合，终边分别与单位圆交于点 $A$ 、 $B$ 两点，点 $A$ 的横坐标为 $\frac{3}{5}$ ，点 $C$ 与点 $B$ 关于 $x$ 轴对称.

(1)、求 $\frac{c o s (2 α - \frac{π}{2})}{s i n^{2} α + c o s 2 α}$ 的值：

(2)、若 $c o s ∠ A O C = - \frac{63}{65}$ ，求 $c o s β$ 的值.

查看试题解析
19. 已知函数 $f (x) = \frac{a^{x} - 1}{a^{x} + a - 1} (a \in R$ ，且 $a \neq 1)$ 是定义在 $R$ 上的奇函数.

(1)、求 $a$ 的值；

(2)、若关于 $t$ 方程 $f (t^{2} - 2 t) + f (4 - k t) = 0$ 在 $[1 ， 3]$ 有且仅有一个根，求实数 $k$ 的取值范围.

查看试题解析
20. 设函数 $f (x) = 2 s i n (x - \frac{π}{3}) ， g (x) = f (x - \frac{π}{6}) \cdot f (x + \frac{π}{6})$

(1)、求函数 $f (x)$ 的对称中心：

(2)、若函数 $g (x)$ 在区间 $[0 ， m]$ 上有最小值 $- 1$ ，求实数 $m$ 的最小值.

查看试题解析
21. 为了进一步增强市场竞争力，某公司计划在2024年利用新技术生产某款运动手表.经过市场调研，生产此款运动手表全年需投入固定成本100万，每生产 $x ($ 单位：千只)手表，需另投入可变成本 $R (x)$ 万元，且 $R (x) = {\begin{array}{l} 2 x^{2} + 80 x + 200 ， 0 < x < 50 ， \\ 201 x + \frac{6400}{x} - 5200 ， x \geq 50 . \end{array}$ 由市场调研知，每部手机售价0.2万元，且全年生产的手机当年能全部销售完.(利润 $=$ 销售额 - 固定成本 - 可变成本)

(1)、求2024年的利润 $W (x)$ (单位：万元) 关于年产量 $x$ (单位：千只) 的函数关系式.

(2)、2024年的年产量为多少 (单位：千只)时，企业所获利润最大? 最大利润是多少?

查看试题解析
22. 已知函数 $f (x) = | x - \frac{3}{x} + 2 | + m$ .

(1)、若函数 $y = f (x)$ 有4个零点 $x_{1} ， x_{2} ， x_{3} ， x_{4} (x_{1} < x_{2} < x_{3} < x_{4})$ ，求证： $x_{1} x_{2} x_{3} x_{4} = 9$ ；

(2)、是否存在非零实数 $m$ ，使得函数 $f (x)$ 在区间 $[a ， b] (0 < a < b)$ 上的取值范围为 $[\frac{2 m}{a} ， \frac{2 m}{b}]$ ? 若存在，求出 $m$ 的取值范围：若不存在，请说明理由.

查看试题解析