四川省南充市2024届高三上学期1月高考适应性考试(一诊)数学(理)试题
试卷更新日期:2024-03-08 类型:高考模拟
一、单项选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 抛物线的准线方程为( )A、 B、 C、 D、2. 当时,复数在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知正方形的边长为1,则( )A、0 B、 C、 D、44. 已知直线m,n和平面 , , , 则“”是“”的( )条件A、充分不必要 B、必要不充分 C、充分必要 D、既不充分也不必要5. 已知全集 , 集合 , , 则能表示A,B,U关系的图是( )A、
 B、
B、 C、
C、 D、
D、 6. 某商品的地区经销商对2023年1月到5月该商品的销售情况进行了调查,得到如下统计表.发现销售量y(万件)与时间x(月)成线性相关,根据表中数据,利用最小二乘法求得y与x的回归直线方程为: . 则下列说法错误的是( )
6. 某商品的地区经销商对2023年1月到5月该商品的销售情况进行了调查,得到如下统计表.发现销售量y(万件)与时间x(月)成线性相关,根据表中数据,利用最小二乘法求得y与x的回归直线方程为: . 则下列说法错误的是( )时间x(月)
1
2
3
4
5
销售量y(万件)
1
1.6
2.0
a
3
A、由回归方程可知2024年1月份该地区的销售量为6.8万件 B、表中数据的样本中心点为 C、 D、由表中数据可知,y和x成正相关7. 二项式的展开式中常数项为( )A、 B、60 C、210 D、8. 已知: , , 则下列说法中错误的是( )A、 B、 C、 D、9. 如图,正方体的棱长为2,E,F分别为 , 的中点,则平面截正方体所得的截面面积为( ) A、 B、 C、9 D、1810. 如图1是函数的部分图象,经过适当的平移和伸缩变换后,得到图2中的部分图象,则( )
A、 B、 C、9 D、1810. 如图1是函数的部分图象,经过适当的平移和伸缩变换后,得到图2中的部分图象,则( )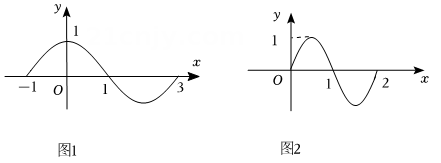 A、 B、 C、方程有4个不相等的实数解 D、的解集为 ,11. 已知双曲线的左右焦点分别为 , , 左右顶点分别为 , , P为双曲线在第一象限上的一点,若 , 则( )A、 B、2 C、5 D、12. 已知函数()有两个不同的零点 , (),下列关于 , 的说法正确的有( )个
A、 B、 C、方程有4个不相等的实数解 D、的解集为 ,11. 已知双曲线的左右焦点分别为 , , 左右顶点分别为 , , P为双曲线在第一象限上的一点,若 , 则( )A、 B、2 C、5 D、12. 已知函数()有两个不同的零点 , (),下列关于 , 的说法正确的有( )个① ② ③ ④
A、1 B、2 C、3 D、4二、填空题:本题共4小题,每小题5分,共20分。
-
13. 满足约束条件的平面区域的面积为 .14. 已知函数为R上的奇函数,且 , 则 .15. 已知圆台的上下底面半径分别为和 , 若存在一个球同时与该圆台的上、下底面及侧面都相切,则该圆台的体积为 .
附:圆台体积公式为:
16. 如图,在中, , , P为内一点,且 , 则 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.必考题:共60分
-
17. 已知数列是首项为2的等比数列,且是和的等差中项.(1)、求的通项公式;(2)、若数列的公比 , 设数列满足 , 求的前2023项和 .18. 2023年秋季,支原体肺炎在全国各地流行,该疾病的主要感染群体为青少年和老年人,某市医院传染病科在该市各医院某段时间就医且年龄在70岁以上的老年人中随机抽查了200人的情况,并将调查结果整理如下:
有慢性疾病
没有慢性疾病
合计
未感染支原体肺炎
60
80
140
感染支原体肺炎
40
20
60
合计
100
100
200
附表:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:(其中)
(1)、是否有99.5%的把握认为70岁以上老人感染支原体肺炎与自身有慢性疾病有关?(2)、现从感染支原体肺炎的60位老人中按分层抽样的方式抽出6人,再从6人中随机抽出4人作为医学研究对象并免费治疗.按以往的经验,有慢性疾病的老人每人的研究治疗费用为2万元,没有慢性疾病的老人每人的研究治疗费用为1万元,记抽出的这4人产生的研究治疗总费用为(单位:万元),求的分布列及数学期望.19. 如图,在四棱锥中,平面 , , , . (1)、求证:平面;(2)、若 , 二面角的正切值为 , 求直线与平面所成角的正弦值.20. 设函数(e为自然对数的底数),函数与函数的图象关于直线对称.(1)、设函数 , 若时,恒成立,求m的取值范围;(2)、证明:与有且仅有两条公切线,且图象上两切点横坐标互为相反数.21. 如图,椭圆的四个顶点为A,B,C,D,过左焦点且斜率为k的直线交椭圆E于M,N两点.
(1)、求证:平面;(2)、若 , 二面角的正切值为 , 求直线与平面所成角的正弦值.20. 设函数(e为自然对数的底数),函数与函数的图象关于直线对称.(1)、设函数 , 若时,恒成立,求m的取值范围;(2)、证明:与有且仅有两条公切线,且图象上两切点横坐标互为相反数.21. 如图,椭圆的四个顶点为A,B,C,D,过左焦点且斜率为k的直线交椭圆E于M,N两点. (1)、求四边形的内切圆的方程;(2)、设 , 连结 , 并延长分别交椭圆E于P,Q两点,设的斜率为 . 则是否存在常数 , 使得恒成立?若存在,求出的值;若不存在,说明理由.
(1)、求四边形的内切圆的方程;(2)、设 , 连结 , 并延长分别交椭圆E于P,Q两点,设的斜率为 . 则是否存在常数 , 使得恒成立?若存在,求出的值;若不存在,说明理由.